
Giant component
Encyclopedia
In network theory
, a giant component is a connected component
of a given random graph
that contains a constant fraction of the entire graph's vertices
.
Giant components are a prominent feature of the Erdős–Rényi model
of random graphs, in which each possible edge connecting pairs of a given set of vertices is present, independently of the other edges, with probability . In this model, if for any constant
for any constant  , then with high probability all connected components of the graph have size , and there is no giant component. However, for
, then with high probability all connected components of the graph have size , and there is no giant component. However, for 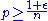 there is with high probability a single giant component, with all other components having size . For
there is with high probability a single giant component, with all other components having size . For 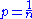 , intermediate between these two possibilities, the number of vertices in the largest component of the graph is with high probability proportional to
, intermediate between these two possibilities, the number of vertices in the largest component of the graph is with high probability proportional to 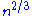 .
.
Alternatively, if one adds randomly selected edges one at a time, starting with an empty graph, then it is not until approximately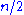 edges have been added that the graph contains a large component, and soon after that the component becomes giant. More precisely, when
edges have been added that the graph contains a large component, and soon after that the component becomes giant. More precisely, when  edges have been added, for values of
edges have been added, for values of  close to but larger than
close to but larger than 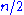 , the size of the giant component is approximately
, the size of the giant component is approximately  . However, according to the coupon collector's problem
. However, according to the coupon collector's problem
,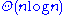 edges are needed in order to have high probability that the whole random graph is connected.
edges are needed in order to have high probability that the whole random graph is connected.
A similar sharp threshold between parameters that lead to graphs with all components small and parameters that lead to a giant component also occurs in random graphs with non-uniform degree distribution
s.
Network theory
Network theory is an area of computer science and network science and part of graph theory. It has application in many disciplines including statistical physics, particle physics, computer science, biology, economics, operations research, and sociology...
, a giant component is a connected component
Connected component
Connected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
of a given random graph
Random graph
In mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
that contains a constant fraction of the entire graph's vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
.
Giant components are a prominent feature of the Erdős–Rényi model
Erdos–Rényi model
In graph theory, the Erdős–Rényi model, named for Paul Erdős and Alfréd Rényi, is either of two models for generating random graphs, including one that sets an edge between each pair of nodes with equal probability, independently of the other edges...
of random graphs, in which each possible edge connecting pairs of a given set of vertices is present, independently of the other edges, with probability . In this model, if
 for any constant
for any constant  , then with high probability all connected components of the graph have size , and there is no giant component. However, for
, then with high probability all connected components of the graph have size , and there is no giant component. However, for 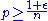 there is with high probability a single giant component, with all other components having size . For
there is with high probability a single giant component, with all other components having size . For 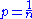 , intermediate between these two possibilities, the number of vertices in the largest component of the graph is with high probability proportional to
, intermediate between these two possibilities, the number of vertices in the largest component of the graph is with high probability proportional to 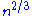 .
.Alternatively, if one adds randomly selected edges one at a time, starting with an empty graph, then it is not until approximately
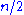 edges have been added that the graph contains a large component, and soon after that the component becomes giant. More precisely, when
edges have been added that the graph contains a large component, and soon after that the component becomes giant. More precisely, when  edges have been added, for values of
edges have been added, for values of  close to but larger than
close to but larger than 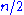 , the size of the giant component is approximately
, the size of the giant component is approximately  . However, according to the coupon collector's problem
. However, according to the coupon collector's problemCoupon collector's problem
In probability theory, the coupon collector's problem describes the "collect all coupons and win" contests. It asks the following question: Suppose that there are n coupons, from which coupons are being collected with replacement...
,
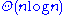 edges are needed in order to have high probability that the whole random graph is connected.
edges are needed in order to have high probability that the whole random graph is connected.A similar sharp threshold between parameters that lead to graphs with all components small and parameters that lead to a giant component also occurs in random graphs with non-uniform degree distribution
Degree distribution
In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network.-Definition:...
s.

