
Oriented coloring
Encyclopedia
In graph theory
, oriented graph coloring is a special type of graph coloring
. Namely, it is
an assignment of "colors" to vertices of an oriented graph that
An oriented chromatic number of a graph G is the least number of colors needed in an oriented coloring;
it is usually denoted by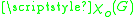 .
.
An oriented graph coloring corresponds to graph homomorphism
into a tournament
.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, oriented graph coloring is a special type of graph coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
. Namely, it is
an assignment of "colors" to vertices of an oriented graph that
- is proper: no two adjacent vertices get the same color, and
- respects the orientation: if (x, y) and (u, v) are arcs of the graph then it is not possible that colors of x and v and of y and u are the same.
An oriented chromatic number of a graph G is the least number of colors needed in an oriented coloring;
it is usually denoted by
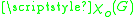 .
.Properties
We need an oriented graph, otherwise no oriented coloring exists. If the graph has loops (directed 2-cycles), the first (second, respectively) condition will be violated.An oriented graph coloring corresponds to graph homomorphism
Graph homomorphism
In the mathematical field of graph theory a graph homomorphism is a mapping between two graphs that respects their structure. More concretely it maps adjacent vertices to adjacent vertices.-Definitions:...
into a tournament
Tournament (graph theory)
A tournament is a directed graph obtained by assigning a direction for each edge in an undirected complete graph. That is, it is a directed graph in which every pair of vertices is connected by a single directed edge....
.

