In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, a weak coloring is a special case of a graph labeling

Graph labeling

In the mathematical discipline of graph theory, a graph labeling is the assignment of labels, traditionally represented by integers, to the edges or vertices, or both, of a graph....

. A weak -coloring of a graph assigns a color to each vertex , such that each non-isolated vertex  is adjacent to at least one vertex with different color. In notation, for each non-isolated , there is a vertex with and .

The figure on the right shows a weak 2-coloring of a graph. Each dark vertex (color 1) is adjacent to at least one light vertex (color 2) and vice versa.

Properties

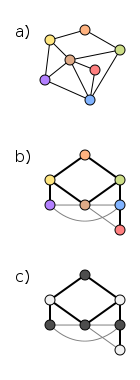
A graph vertex coloring is a weak coloring, but not necessarily vice versa.

Every graph has a weak 2-coloring. The figure on the right illustrates a simple algorithm for constructing a weak 2-coloring in an arbitrary graph. Part (a) shows the original graph. Part (b) shows a breadth-first search

Breadth-first search

In graph theory, breadth-first search is a graph search algorithm that begins at the root node and explores all the neighboring nodes...

 tree of the same graph. Part (c) shows how to color the tree: starting from the root, the layers of the tree are colored alternatingly with colors 1 (dark) and 2 (light).

If there is no isolated vertex in the graph , then a weak 2-coloring determines a domatic partition: the set of the nodes with is a dominating set

Dominating set

In graph theory, a dominating set for a graph G =  is a subset D of V such that every vertex not in D is joined to at least one member of D by some edge...

, and the set of the nodes with is another dominating set.

Applications

Historically, weak coloring served as the first non-trivial example of a graph problem that can be solved with a local algorithm (a distributed algorithm that runs in a constant number of synchronous communication rounds). More precisely, if the degree

Degree (graph theory)

In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...

 of each node is odd and bounded by a constant, then there is a constant-time distributed algorithm for weak 2-coloring.

This is different from (non-weak) vertex coloring: there is no constant-time distributed algorithm for vertex coloring; the best possible algorithms require communication rounds. Here is the iterated logarithm

Iterated logarithm

In computer science, the iterated logarithm of n, written  n , is the number of times the logarithm function must be iteratively applied before the result is less than or equal to 1...

of .