Equitable coloring
Encyclopedia
In graph theory
, an area of mathematics, an equitable coloring is an assignment of colors
to the vertices
of an undirected graph, in such a way that
That is, the partition of vertices among the different colors is as uniform as possible. For instance, giving each vertex a distinct color would be equitable, but would typically use many more colors than are necessary in an optimal equitable coloring. An equivalent way of defining an equitable coloring is that it is an embedding of the given graph as a subgraph of a Turán graph
. There are two kinds of chromatic number associated with equitable coloring. The equitable chromatic number of a graph G is the smallest number k such that G has an equitable coloring with k colors. But G might not have equitable colorings for some larger numbers of colors; the equitable chromatic threshold of G is the smallest k such that G has equitable colorings for any number of colors greater than or equal to k.
The Hajnal–Szemerédi theorem, posed as a conjecture by and proven by , states that any graph with maximum degree Δ has an equitable coloring with Δ + 1 colors. Several related conjectures remain open. Polynomial time algorithms are also known for finding a coloring matching this bound, and for finding optimal colorings of special classes of graphs, but the more general problem of finding an equitable coloring of an arbitrary graph with a given number of colors is NP-complete
.
K1,5 shown in the illustration is a complete bipartite graph
, and therefore may be colored with two colors. However, the resulting coloring has one vertex in one color class and five in another, and is therefore not equitable. The smallest number of colors in an equitable coloring of this graph is four, as shown in the illustration: the central vertex must be the only vertex in its color class, so the other five vertices must be split among at least three color classes in order to ensure that the other color classes all have at most two vertices. More generally, observes that any star K1,n needs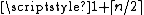
colors in any equitable coloring; thus, the chromatic number of a graph may differ from its equitable coloring number by a factor as large as n/4. Because K1,5 has maximum degree five, the number of colors guaranteed for it by the Hajnal–Szemerédi theorem is six, achieved by giving each vertex a distinct color.
Another interesting phenomenon is exhibited by a different complete bipartite graph, K2n + 1,2n + 1. This graph has an equitable 2-coloring, given by its bipartition. However, it does not have an equitable (2n + 1)-coloring: any equitable partition of the vertices into that many color classes would have to have exactly two vertices per class, but the two sides of the bipartition cannot each be partitioned into pairs because they have an odd number of vertices. Therefore, the equitable chromatic threshold of this graph is 2n + 2, significantly greater than its equitable chromatic number of two.
s and odd cycles). However, this coloring may in general be far from equitable. conjectured
that an equitable coloring is possible with only one more color: any graph with maximum degree Δ has an equitable coloring with Δ + 1 colors. The case Δ = 2 is straightforward (any union of paths and cycles may be equitably colored by using a repeated pattern of three colors, with minor adjustments to the repetition when closing a cycle) and the case Δ + 1= n/3 had previously been solved by . The full conjecture was proven by , and is now known as the Hajnal–Szemerédi theorem. Their original proof was long and complicated; a simpler proof was given by . A polynomial time algorithm for finding equitable colorings with this many colors was described by Kierstead and Kostochka; they credit Marcelo Mydlarz and Endre Szemerédi with a prior unpublished polynomial time algorithm. Kierstead and Kostochka also announce but do not prove a strengthening of the theorem, to show that an equitable k-coloring exists whenever every two adjacent vertices have degrees adding to at most 2k + 1.
conjectured a form of Brooks' theorem for equitable coloring: every graph with maximum degree Δ has an equitable coloring with Δ or fewer colors, with the exceptions of complete graphs and odd cycles. A strengthened version of the conjecture states that each such graph has an equitable coloring with exactly Δ colors, with one additional exception, a complete bipartite graph
in which both sides of the bipartition have the same odd number of vertices.
proposed a strengthening of the Hajnal–Szemerédi theorem that also subsumes Dirac
's theorem that dense graph
s are Hamiltonian
: he conjectured that, if every vertex in an n-vertex graph has at least kn/(k + 1) neighbors, then the graph contains as a subgraph the graph formed by connecting vertices that are at most k steps apart in an n-cycle. The case k = 1 is Dirac's theorem itself. The Hajnal–Szemerédi theorem may be recovered from this conjecture by applying the conjecture for larger values of k to the complement graph
of a given graph, and using as color classes contiguous subsequences of vertices from the n-cycle. Seymour's conjecture has been proven for graph in which n is sufficiently large relative to k; the proof uses several deep tools including the Hajnal–Szemerédi theorem itself.
Yet another generalization of the Hajnal–Szemerédi theorem is the Catlin–Bollobás–Eldridge conjecture. This states that if G1 and G2 are graphs on n vertices with maximum degree Δ1 and Δ2 respectively, and if (Δ1 + 1)(Δ2 + 1) ≤ n, then G1 and G2 can be packed. That is, G1 and G2 can be represented on the same set of n vertices with no edges in common. The Hajnal–Szemerédi theorem is the special case of this conjecture in which G2 is a disjoint union of cliques
. provides a similar but stronger condition on Δ1 and Δ2 under which such a packing can be guaranteed to exist.
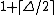
with the worst case occurring for a star. However, most trees have significantly smaller equitable chromatic number: if a tree with n vertices has Δ ≤ n/3 − O(1), then it has an equitable coloring with only three colors. studies the equitable chromatic number of graph products.
to equitable coloring may be proven by adding sufficiently many isolated vertices to a graph, showing that it is NP-complete
to test whether a graph has an equitable coloring with a given number of colors (greater than two). However, the problem becomes more interesting when restricted to special classes of graphs or from the point of view of parameterized complexity
. showed that, given a graph G and a number c of colors, it is possible to test whether G admits an equitable c-coloring in time O(nO(t)), where t is the treewidth of G; in particular, equitable coloring may be solved optimally in polynomial time for trees
(previously known due to ) and outerplanar graph
s. A polynomial time algorithm is also known for equitable coloring of split graph
s. However, prove that, when the treewidth is a parameter to the algorithm, the problem is W[1]-hard. Thus, it is unlikely that there exists a polynomial time algorithm independent of this parameter, or even that the dependence on the parameter may be moved out of the exponent in the formula for the running time.
problems. In this application, the vertices of a graph represent a collection of tasks to be performed, and an edge connects two tasks that should not be performed at the same time. A coloring of this graph represents a partition of the tasks into subsets that may be performed simultaneously; thus, the number of colors in the coloring corresponds to the number of time steps required to perform the entire task. Due to load balancing
considerations, it is desirable to perform equal or nearly-equal numbers of tasks in each time step, and this balancing is exactly what an equitable coloring achieves. mentions a specific application of this type of scheduling problem, assigning university courses to time slots in a way that spreads the courses evenly among the available time slots and avoids scheduling incompatible pairs of courses at the same time as each other.
The Hajnal-Szemerédi theorem has also been used to bound the variance
of sums of random variables with limited dependence . If (as in the setup for the Lovász local lemma
) each variable depends on at most Δ others, an equitable coloring of the dependence graph may be used to partition the variables into independent subsets within which Chernoff bound
s may be calculated, resulting in tighter overall bounds on the variance than if the partition were performed in a non-equitable way.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, an area of mathematics, an equitable coloring is an assignment of colors
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
to the vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
of an undirected graph, in such a way that
- No two adjacent vertices have the same color, and
- The numbers of vertices in any two color classes differ by at most one.
That is, the partition of vertices among the different colors is as uniform as possible. For instance, giving each vertex a distinct color would be equitable, but would typically use many more colors than are necessary in an optimal equitable coloring. An equivalent way of defining an equitable coloring is that it is an embedding of the given graph as a subgraph of a Turán graph
Turán graph
The Turán graph T is a graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge whenever they belong to different subsets. The graph will have subsets of size \lceil n/r\rceil, and r- subsets of size \lfloor n/r\rfloor...
. There are two kinds of chromatic number associated with equitable coloring. The equitable chromatic number of a graph G is the smallest number k such that G has an equitable coloring with k colors. But G might not have equitable colorings for some larger numbers of colors; the equitable chromatic threshold of G is the smallest k such that G has equitable colorings for any number of colors greater than or equal to k.
The Hajnal–Szemerédi theorem, posed as a conjecture by and proven by , states that any graph with maximum degree Δ has an equitable coloring with Δ + 1 colors. Several related conjectures remain open. Polynomial time algorithms are also known for finding a coloring matching this bound, and for finding optimal colorings of special classes of graphs, but the more general problem of finding an equitable coloring of an arbitrary graph with a given number of colors is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
.
Examples
The starStar (graph theory)
In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves...
K1,5 shown in the illustration is a complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
, and therefore may be colored with two colors. However, the resulting coloring has one vertex in one color class and five in another, and is therefore not equitable. The smallest number of colors in an equitable coloring of this graph is four, as shown in the illustration: the central vertex must be the only vertex in its color class, so the other five vertices must be split among at least three color classes in order to ensure that the other color classes all have at most two vertices. More generally, observes that any star K1,n needs
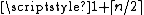colors in any equitable coloring; thus, the chromatic number of a graph may differ from its equitable coloring number by a factor as large as n/4. Because K1,5 has maximum degree five, the number of colors guaranteed for it by the Hajnal–Szemerédi theorem is six, achieved by giving each vertex a distinct color.Another interesting phenomenon is exhibited by a different complete bipartite graph, K2n + 1,2n + 1. This graph has an equitable 2-coloring, given by its bipartition. However, it does not have an equitable (2n + 1)-coloring: any equitable partition of the vertices into that many color classes would have to have exactly two vertices per class, but the two sides of the bipartition cannot each be partitioned into pairs because they have an odd number of vertices. Therefore, the equitable chromatic threshold of this graph is 2n + 2, significantly greater than its equitable chromatic number of two.
Hajnal–Szemerédi theorem
Brooks' theorem states that any graph with maximum degree Δ has a Δ-coloring, with two exceptions (complete graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
s and odd cycles). However, this coloring may in general be far from equitable. conjectured
Erdos conjecture
The prolific mathematician Paul Erdős and his various collaborators made many famous mathematical conjectures, over a wide field of subjects.Some of these are the following:* The Cameron–Erdős conjecture on sum-free sets of integers, proved by Ben Green....
that an equitable coloring is possible with only one more color: any graph with maximum degree Δ has an equitable coloring with Δ + 1 colors. The case Δ = 2 is straightforward (any union of paths and cycles may be equitably colored by using a repeated pattern of three colors, with minor adjustments to the repetition when closing a cycle) and the case Δ + 1= n/3 had previously been solved by . The full conjecture was proven by , and is now known as the Hajnal–Szemerédi theorem. Their original proof was long and complicated; a simpler proof was given by . A polynomial time algorithm for finding equitable colorings with this many colors was described by Kierstead and Kostochka; they credit Marcelo Mydlarz and Endre Szemerédi with a prior unpublished polynomial time algorithm. Kierstead and Kostochka also announce but do not prove a strengthening of the theorem, to show that an equitable k-coloring exists whenever every two adjacent vertices have degrees adding to at most 2k + 1.
conjectured a form of Brooks' theorem for equitable coloring: every graph with maximum degree Δ has an equitable coloring with Δ or fewer colors, with the exceptions of complete graphs and odd cycles. A strengthened version of the conjecture states that each such graph has an equitable coloring with exactly Δ colors, with one additional exception, a complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
in which both sides of the bipartition have the same odd number of vertices.
proposed a strengthening of the Hajnal–Szemerédi theorem that also subsumes Dirac
Gabriel Andrew Dirac
Gabriel Andrew Dirac was a mathematician who mainly worked in graph theory. He stated a sufficient condition for a graph to contain a Hamiltonian circuit.Dirac received his Ph.D...
's theorem that dense graph
Dense graph
In mathematics, a dense graph is a graph in which the number of edges is close to the maximal number of edges. The opposite, a graph with only a few edges, is a sparse graph...
s are Hamiltonian
Hamiltonian path
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle in an undirected graph that visits each vertex exactly once and also returns to the starting vertex...
: he conjectured that, if every vertex in an n-vertex graph has at least kn/(k + 1) neighbors, then the graph contains as a subgraph the graph formed by connecting vertices that are at most k steps apart in an n-cycle. The case k = 1 is Dirac's theorem itself. The Hajnal–Szemerédi theorem may be recovered from this conjecture by applying the conjecture for larger values of k to the complement graph
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of a given graph, and using as color classes contiguous subsequences of vertices from the n-cycle. Seymour's conjecture has been proven for graph in which n is sufficiently large relative to k; the proof uses several deep tools including the Hajnal–Szemerédi theorem itself.
Yet another generalization of the Hajnal–Szemerédi theorem is the Catlin–Bollobás–Eldridge conjecture. This states that if G1 and G2 are graphs on n vertices with maximum degree Δ1 and Δ2 respectively, and if (Δ1 + 1)(Δ2 + 1) ≤ n, then G1 and G2 can be packed. That is, G1 and G2 can be represented on the same set of n vertices with no edges in common. The Hajnal–Szemerédi theorem is the special case of this conjecture in which G2 is a disjoint union of cliques
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
. provides a similar but stronger condition on Δ1 and Δ2 under which such a packing can be guaranteed to exist.
Special classes of graphs
For any tree with maximum degree Δ, the equitable chromatic number is at most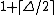with the worst case occurring for a star. However, most trees have significantly smaller equitable chromatic number: if a tree with n vertices has Δ ≤ n/3 − O(1), then it has an equitable coloring with only three colors. studies the equitable chromatic number of graph products.
Computational complexity
The problem of finding equitable colorings with as few colorings as possible (below the Hajnal-Szemerédi bound) has also been studied. A straightforward reduction from graph coloringGraph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
to equitable coloring may be proven by adding sufficiently many isolated vertices to a graph, showing that it is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
to test whether a graph has an equitable coloring with a given number of colors (greater than two). However, the problem becomes more interesting when restricted to special classes of graphs or from the point of view of parameterized complexity
Parameterized complexity
Parameterized complexity is a branch of computational complexity theory in computer science that focuses on classifying computational problems according to their inherent difficulty with respect to multiple parameters of the input. The complexity of a problem is then measured as a function in those...
. showed that, given a graph G and a number c of colors, it is possible to test whether G admits an equitable c-coloring in time O(nO(t)), where t is the treewidth of G; in particular, equitable coloring may be solved optimally in polynomial time for trees
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
(previously known due to ) and outerplanar graph
Outerplanar graph
In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...
s. A polynomial time algorithm is also known for equitable coloring of split graph
Split graph
In graph theory, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique and an independent set...
s. However, prove that, when the treewidth is a parameter to the algorithm, the problem is W[1]-hard. Thus, it is unlikely that there exists a polynomial time algorithm independent of this parameter, or even that the dependence on the parameter may be moved out of the exponent in the formula for the running time.
Applications
One motivation for equitable coloring suggested by concerns schedulingJob Shop Scheduling
Job shop scheduling is an optimization problem in computer science in which ideal jobs are assigned to resources at particular times. The most basic version is as follows:...
problems. In this application, the vertices of a graph represent a collection of tasks to be performed, and an edge connects two tasks that should not be performed at the same time. A coloring of this graph represents a partition of the tasks into subsets that may be performed simultaneously; thus, the number of colors in the coloring corresponds to the number of time steps required to perform the entire task. Due to load balancing
Load balancing
Load balancing or load distribution may refer to:*Load balancing , balancing a workload amongst multiple computer devices*Load balancing , the storing of excess electrical power by power stations during low demand periods, for release as demand rises*Weight distribution, the apportioning of weight...
considerations, it is desirable to perform equal or nearly-equal numbers of tasks in each time step, and this balancing is exactly what an equitable coloring achieves. mentions a specific application of this type of scheduling problem, assigning university courses to time slots in a way that spreads the courses evenly among the available time slots and avoids scheduling incompatible pairs of courses at the same time as each other.
The Hajnal-Szemerédi theorem has also been used to bound the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of sums of random variables with limited dependence . If (as in the setup for the Lovász local lemma
Lovász local lemma
In probability theory, if a large number of events are all independent of one another and each has probability less than 1, then there is a positive probability that none of the events will occur...
) each variable depends on at most Δ others, an equitable coloring of the dependence graph may be used to partition the variables into independent subsets within which Chernoff bound
Chernoff bound
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
s may be calculated, resulting in tighter overall bounds on the variance than if the partition were performed in a non-equitable way.
External links
- ECOPT A Branch and Cut algorithm for solving the Equitable Coloring Problem