
William Rowan Hamilton
Encyclopedia
Sir
William Rowan Hamilton (4 August 1805 – 2 September 1865) was an Irish
physicist
, astronomer
, and mathematician
, who made important contributions to classical mechanics
, optics
, and algebra
. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques. His greatest contribution is perhaps the reformulation of Newtonian mechanics, now called Hamiltonian mechanics
. This work has proven central to the modern study of classical field theories such as electromagnetism
, and to the development of quantum mechanics
. In mathematics, he is perhaps best known as the inventor of quaternion
s. Hamilton is said to have shown immense talent at a very early age, prompting astronomer Bishop Dr. John Brinkley
to remark in 1823 of Hamilton at the age of 18: “This young man, I do not say will be, but is, the first mathematician of his age.”
, classical mechanics
, adaptation of dynamic methods in optical systems, applying quaternion and vector methods to problems in mechanics and in geometry, development of theories of conjugate algebraic couple functions (in which complex numbers are constructed as ordered pairs of real numbers), solvability of polynomial equations and general quintic polynomial solvable by radicals, the analysis on Fluctuating Functions (and the ideas from Fourier analysis), linear operators on quaternions and proving a result for linear operators on the space of quaternions (which is a special case of the general theorem which today is known as the Cayley–Hamilton theorem
). Hamilton also invented "Icosian Calculus
", which he used to investigate closed edge paths on a dodecahedron that visit each vertex exactly once.
, worked as a solicitor. By the age of three, Hamilton had been sent to live with his uncle James Hamilton, a graduate of Trinity College
who ran a school in Talbots Castle. His uncle soon discovered that Hamilton had a remarkable ability to learn languages.
At a young age, Hamilton displayed an uncanny ability to acquire languages (although this is disputed by some historians, who claim he had only a very basic understanding of them). At the age of seven he had already made very considerable progress in Hebrew
, and before he was thirteen he had acquired, under the care of his uncle (a linguist), almost as many languages as he had years of age. These included the classical and modern European languages, and Persian
, Arabic
, Hindustani
, Sanskrit
, and even Marathi
and Malay
. He retained much of his knowledge of languages to the end of his life, often reading Persian and Arabic in his spare time, although he had long stopped studying languages, and used them just for relaxation.
At the age of 12, Hamilton met and competed with mathematical savant
Zerah Colburn
in mental arithmetic, whilst Colburn was in Dublin displaying his talents. Colburn more often than not came away the victor, which impressed Hamilton who was not used to being beaten in any contest of intellect. Hamilton was part of a small but well-regarded school of mathematicians associated with Trinity College, Dublin
, which he entered at age 18 and where he spent his life. He studied both classics and science, and was appointed Professor of Astronomy
in 1827, prior to his graduation.
and to classical mechanics
. His first discovery was in an early paper that he communicated in 1823 to Dr. Brinkley, who presented it under the title of "Caustics" in 1824 to the Royal Irish Academy
. It was referred as usual to a committee. While their report acknowledged its novelty and value, they recommended further development and simplification before publication. Between 1825 to 1828 the paper grew to an immense size, mostly by the additional details which the committee had suggested. But it also became more intelligible, and the features of the new method were now easily to be seen. Until this period Hamilton himself seems not to have fully understood either the nature or importance of optics, as later he intended to apply his method to dynamics.
In 1827, Hamilton presented a theory of a single function, now known as Hamilton's principal function, that brings together mechanics, optics, and mathematics, and which helped to establish the wave theory of light. He proposed for it when he first predicted its existence in the third supplement to his "Systems of Rays", read in 1832. The Royal Irish Academy paper was finally entitled “Theory of Systems of Rays,” (23 April 1827) and the first part was printed in 1828 in the Transactions of the Royal Irish Academy. The more important contents of the second and third parts appeared in the three voluminous supplements (to the first part) which were published in the same Transactions, and in the two papers “On a General Method in Dynamics,” which appeared in the Philosophical Transactions in 1834 and 1835. In these papers, Hamilton developed his great principle of “Varying Action“. The most remarkable result of this work is the prediction that a single ray of light entering a biaxial crystal at a certain angle would emerge as a hollow cone of rays. This discovery is still known by its original name, "conical refraction".
The step from optics to dynamics in the application of the method of “Varying Action” was made in 1827, and communicated to the Royal Society, in whose Philosophical Transactions for 1834 and 1835 there are two papers on the subject, which, like the “Systems of Rays,” display a mastery over symbols and a flow of mathematical language almost unequaled. The common thread running through all this work is Hamilton's principle of “Varying Action“. Although it is based on the calculus of variations
and may be said to belong to the general class of problems included under the principle of least action
which had been studied earlier by Pierre Louis Maupertuis
, Euler, Joseph Louis Lagrange
, and others, Hamilton's analysis revealed much deeper mathematical structure than had been previously understood, in particular the symmetry between momentum and position. Paradoxically, the credit for discovering the quantity now called the Lagrangian
and Lagrange's equations belongs to Hamilton. Hamilton's advances enlarged greatly the class of mechanical problems that could be solved, and they represent perhaps the greatest addition which dynamics
had received since the work of Isaac Newton
and Lagrange
. Many scientists, including Liouville
, Jacobi, Darboux
, Poincaré
, Kolmogorov, and Arnold, have extended Hamilton's work, thereby expanding our knowledge of mechanics
and differential equations.
While Hamilton's reformulation of classical mechanics is based on the same physical principles as the mechanics of Newton and Lagrange, it provides a powerful new technique for working with the equations of motion. More importantly, both the Lagrangian
and Hamiltonian
approaches which were initially developed to describe the motion of discrete system
s, have proven critical to the study of continuous classical systems in physics, and even quantum mechanical systems. In this way, the techniques find use in electromagnetism
, quantum mechanics
, quantum
relativity theory, and quantum field theory
.
studies seem to have been undertaken and carried to their full development without any assistance whatsoever, and the result is that his writings do not belong to any particular "school". Not only was Hamilton an expert as an arithmetic
calculator, but he seems to have occasionally had fun in working out the result of some calculation to an enormous number of decimal places. At the age of twelve Hamilton engaged Zerah Colburn
, the American
"calculating boy
", who was then being exhibited as a curiosity in Dublin, and did not always lose. Two years before, he had stumbled into a Latin
copy of Euclid
, which he eagerly devoured; and at twelve Hamilton studied Newton
’s Arithmetica Universalis
. This was his introduction to modern analysis
. Hamilton soon began to read the Principia
, and at sixteen Hamilton had mastered a great part of it, as well as some more modern works on analytical geometry and the differential calculus
.
Around this time Hamilton was also preparing to enter Trinity College
, Dublin, and therefore had to devote some time to classics. In mid-1822 he began a systematic study of Laplace's Mécanique Céleste
.
From that time Hamilton appears to have devoted himself almost wholly to mathematics, though he always kept himself well acquainted with the progress of science
both in Britain and abroad. Hamilton found an important defect in one of Laplace’s demonstrations, and he was induced by a friend to write out his remarks, so that they could be shown to Dr. John Brinkley
, then the first Astronomer Royal for Ireland
, and an accomplished mathematician
. Brinkley seems to have immediately perceived Hamilton's talents, and to have encouraged him in the kindest way.
Hamilton’s career at College was perhaps unexampled. Amongst a number of extraordinary competitors, he was first in every subject and at every examination. He achieved the rare distinction of obtaining an optime both for Greek
and for physics
. Hamilton might have attained many more such honours (he was expected to win both the gold medal
s at the degree examination), if his career as a student had not been cut short by an unprecedented event. This was Hamilton’s appointment to the Andrews Professorship of Astronomy in the University of Dublin
, vacated by Dr. Brinkley in 1827. The chair was not exactly offered to him, as has been sometimes asserted, but the electors, having met and talked over the subject, authorized Hamilton's personal friend (also an elector) to urge Hamilton to become a candidate, a step which Hamilton's modesty had prevented him from taking. Thus, when barely 22, Hamilton was established at the Dunsink Observatory
, near Dublin.
Hamilton was not especially suited for the post, because although he had a profound acquaintance with theoretical astronomy
, he had paid little attention to the regular work of the practical astronomer
. Hamilton’s time was better employed in original investigations than it would have been spent in observations made even with the best of instruments. Hamilton was intended by the university authorities who elected him to the professorship of astronomy to spend his time as he best could for the advancement of science
, without being tied down to any particular branch. If Hamilton had devoted himself to practical astronomy, the University of Dublin would assuredly have furnished him with instruments and an adequate staff of assistants.
In 1835, being secretary to the meeting of the British Association
which was held that year in Dublin, he was knight
ed by the lord-lieutenant
. Other honours rapidly succeeded, among which his election in 1837 to the president
’s chair in the Royal Irish Academy
, and the rare distinction of being made a corresponding member of the Saint Petersburg Academy of Sciences. Later, in 1864, the newly established United States National Academy of Sciences
elected its first Foreign Associates, and decided to put Hamilton's name on top of their list.
s in 1843. However, in 1840, Benjamin Olinde Rodrigues had already reached a result that amounted to their discovery in all but name.
Hamilton was looking for ways of extending complex number
s (which can be viewed as points
on a 2-dimensional plane
) to higher spatial dimensions.
He failed to find a useful 3-dimensional system (in modern terminology, he failed to find a real, three dimensional skew-field), but in working with four dimensions he created quaternions. According to Hamilton, on 16 October he was out walking along the Royal Canal in Dublin with his wife when the solution in the form of the equation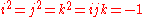
suddenly occurred to him; Hamilton then promptly carved this equation using his penknife into the side of the nearby Broom Bridge
(which Hamilton called Brougham Bridge), for fear he would forget it. This event marks the discovery of the quaternion group
.
A plaque under the bridge, was unveiled by the Taoiseach Éamon de Valera
(himself a mathematician and student of quaternions), on November 13, 1958.
Since 1989, the National University of Ireland, Maynooth
has organized a pilgrimage, where mathematicians take a walk from Dunsink Observatory to the bridge, where no trace of the carving remains, though a stone plaque does commemorate the discovery.
The quaternion involved abandoning commutativity
, a radical step for the time. Not only this, but Hamilton had in a sense invented the cross and dot products of vector algebra. Hamilton also described a quaternion as an ordered four-element multiple of real numbers, and described the first element as the 'scalar' part, and the remaining three as the 'vector' part.
Hamilton introduced, as a method of analysis, both quaternions and biquaternions, the extension to eight dimensions by introduction of complex number coefficient
s. When his work was assembled in 1853, the book Lectures on Quaternions had "formed the subject of successive courses of lectures, delivered in 1848 and subsequent years, in the Halls of Trinity College, Dublin". Hamilton confidently declared that quaternions would be found to have a powerful influence as an instrument of research.
When he died, Hamilton was working on a definitive statement of quaternion science. His son William Edwin Hamilton brought the Elements of Quaternions, a hefty volume of 762 pages, to publication in 1866. As copies ran short, a second edition was prepared by Charles Jasper Joly
, when the book was split into two volumes, the first appearing 1899 and the second in 1901. The subject index and footnotes in this second edition improved the Elements accessibility.
Peter Guthrie Tait
among others, advocated the use of Hamilton's quaternions. They were made a mandatory examination topic in Dublin, and for a while they were the only advanced mathematics taught in some American
universities. However, controversy about the use of quaternions grew in the late 19th century. Some of Hamilton's supporters vociferously opposed the growing fields of vector algebra and vector calculus (from developers like Oliver Heaviside
and Josiah Willard Gibbs
), because quaternions provide superior notation. While this is undeniable for four dimensions, quaternions cannot be used with arbitrary dimensionality (though extensions like Clifford algebra
s can). Vector notation had largely replaced the "space-time" quaternions in science and engineering by the mid-20th century.
Today, the quaternions are in use by computer graphics
, control theory
, signal processing
, and orbital mechanics, mainly for representing rotations/orientations. For example, it is common for spacecraft attitude-control systems to be commanded in terms of quaternions, which are also used to telemeter their current attitude. The rationale is that combining many quaternion transformations is more numerically stable than combining many matrix transformations. In pure mathematics, quaternions show up significantly as one of the four finite-dimensional normed division algebra
s over the real numbers, with applications throughout algebra and geometry.
, the previous mentioned works barely form the greater portion of what Hamilton has published. Hamilton developed the variational principle
, which was reformulated later by Carl Gustav Jacob Jacobi. He also introduced the Icosian game
or Hamilton's puzzle which can be solved using the concept of a Hamiltonian path
.
Hamilton's extraordinary investigations connected with the solution of algebraic equations of the fifth degree
, and his examination of the results arrived at by N. H. Abel
, G. B. Jerrard, and others in their researches on this subject, form another contribution to science. There is next Hamilton's paper on fluctuating functions, a subject which, since the time of Joseph Fourier
, has been of immense and ever increasing value in physical applications of mathematics. There is also the extremely ingenious invention of the hodograph
. Of his extensive investigations into the solutions (especially by numerical approximation) of certain classes of physical differential equations, only a few items have been published, at intervals, in the Philosophical Magazine
.
Besides all this, Hamilton was a voluminous correspondent. Often a single letter of Hamilton's occupied from fifty to a hundred or more closely written pages, all devoted to the minute consideration of every feature of some particular problem; for it was one of the peculiar characteristics of Hamilton's mind never to be satisfied with a general understanding of a question; Hamilton pursued the problem until he knew it in all its details. Hamilton was ever courteous and kind in answering applications for assistance in the study of his works, even when his compliance must have cost him much time. He was excessively precise and hard to please with reference to the final polish of his own works for publication; and it was probably for this reason that he published so little compared with the extent of his investigations.
 Hamilton retained his faculties unimpaired to the very last, and steadily continued the task of finishing the Elements of Quaternions which had occupied the last six years of his life. He died on September 2, 1865, following a severe attack of gout
Hamilton retained his faculties unimpaired to the very last, and steadily continued the task of finishing the Elements of Quaternions which had occupied the last six years of his life. He died on September 2, 1865, following a severe attack of gout
precipitated by excessive drinking and overeating. He is buried in Mount Jerome Cemetery
in Dublin.
Hamilton is recognized as one of Ireland's leading scientists and, as Ireland becomes more aware of its scientific heritage, he is increasingly celebrated. The Hamilton Institute is an applied mathematics research institute at NUI Maynooth
and the Royal Irish Academy
holds an annual public Hamilton lecture at which Murray Gell-Mann
, Frank Wilczek
, Andrew Wiles
, and Timothy Gowers have all spoken. The year 2005 was the 200th anniversary of Hamilton's birth and the Irish government designated that the Hamilton Year, celebrating Irish science. Trinity College Dublin marked the year by launching the Hamilton Mathematics Institute TCD.
A commemorative coin was issued by the Central Bank of Ireland in his honour.
Publications
Sir
Sir is an honorific used as a title , or as a courtesy title to address a man without using his given or family name in many English speaking cultures...
William Rowan Hamilton (4 August 1805 – 2 September 1865) was an Irish
Ireland
Ireland is an island to the northwest of continental Europe. It is the third-largest island in Europe and the twentieth-largest island on Earth...
physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
, astronomer
Astronomer
An astronomer is a scientist who studies celestial bodies such as planets, stars and galaxies.Historically, astronomy was more concerned with the classification and description of phenomena in the sky, while astrophysics attempted to explain these phenomena and the differences between them using...
, and mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, who made important contributions to classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, and algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques. His greatest contribution is perhaps the reformulation of Newtonian mechanics, now called Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
. This work has proven central to the modern study of classical field theories such as electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, and to the development of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. In mathematics, he is perhaps best known as the inventor of quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s. Hamilton is said to have shown immense talent at a very early age, prompting astronomer Bishop Dr. John Brinkley
John Brinkley (astronomer)
The Rt. Rev. John Mortimer Brinkley D.D. was the first Royal Astronomer of Ireland and later Bishop of Cloyne.-Early years:...
to remark in 1823 of Hamilton at the age of 18: “This young man, I do not say will be, but is, the first mathematician of his age.”
Life
William Rowan Hamilton's scientific career included the study of geometrical opticsGeometrical optics
Geometrical optics, or ray optics, describes light propagation in terms of "rays". The "ray" in geometric optics is an abstraction, or "instrument", which can be used to approximately model how light will propagate. Light rays are defined to propagate in a rectilinear path as far as they travel in...
, classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, adaptation of dynamic methods in optical systems, applying quaternion and vector methods to problems in mechanics and in geometry, development of theories of conjugate algebraic couple functions (in which complex numbers are constructed as ordered pairs of real numbers), solvability of polynomial equations and general quintic polynomial solvable by radicals, the analysis on Fluctuating Functions (and the ideas from Fourier analysis), linear operators on quaternions and proving a result for linear operators on the space of quaternions (which is a special case of the general theorem which today is known as the Cayley–Hamilton theorem
Cayley–Hamilton theorem
In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....
). Hamilton also invented "Icosian Calculus
Icosian Calculus
The Icosian Calculus is a non-commutative algebraic structure discovered by the Irish mathematician William Rowan Hamilton in 1856.In modern terms, he gave a group presentation of the icosahedral rotation group by generators and relations....
", which he used to investigate closed edge paths on a dodecahedron that visit each vertex exactly once.
Early life
Hamilton was the fourth of nine children born to Sarah Hutton (1780–1817) and Archibald Hamilton (1778–1819), who lived in Dublin at 38 Dominick Street. Hamilton's father, who was from DunboyneDunboyne
Dunboyne is a town in County Meath in Ireland. For the most part, it is a dormitory town for the city of Dublin.-Location:Dunboyne is centred on the crossroads formed by the R156 regional road and the old Maynooth Road ....
, worked as a solicitor. By the age of three, Hamilton had been sent to live with his uncle James Hamilton, a graduate of Trinity College
Trinity College, Dublin
Trinity College, Dublin , formally known as the College of the Holy and Undivided Trinity of Queen Elizabeth near Dublin, was founded in 1592 by letters patent from Queen Elizabeth I as the "mother of a university", Extracts from Letters Patent of Elizabeth I, 1592: "...we...found and...
who ran a school in Talbots Castle. His uncle soon discovered that Hamilton had a remarkable ability to learn languages.
At a young age, Hamilton displayed an uncanny ability to acquire languages (although this is disputed by some historians, who claim he had only a very basic understanding of them). At the age of seven he had already made very considerable progress in Hebrew
Hebrew language
Hebrew is a Semitic language of the Afroasiatic language family. Culturally, is it considered by Jews and other religious groups as the language of the Jewish people, though other Jewish languages had originated among diaspora Jews, and the Hebrew language is also used by non-Jewish groups, such...
, and before he was thirteen he had acquired, under the care of his uncle (a linguist), almost as many languages as he had years of age. These included the classical and modern European languages, and Persian
Persian language
Persian is an Iranian language within the Indo-Iranian branch of the Indo-European languages. It is primarily spoken in Iran, Afghanistan, Tajikistan and countries which historically came under Persian influence...
, Arabic
Arabic language
Arabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
, Hindustani
Hindustani language
Hindi-Urdu is an Indo-Aryan language and the lingua franca of North India and Pakistan. It is also known as Hindustani , and historically, as Hindavi or Rekhta...
, Sanskrit
Sanskrit
Sanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
, and even Marathi
Marathi language
Marathi is an Indo-Aryan language spoken by the Marathi people of western and central India. It is the official language of the state of Maharashtra. There are over 68 million fluent speakers worldwide. Marathi has the fourth largest number of native speakers in India and is the fifteenth most...
and Malay
Malay language
Malay is a major language of the Austronesian family. It is the official language of Malaysia , Indonesia , Brunei and Singapore...
. He retained much of his knowledge of languages to the end of his life, often reading Persian and Arabic in his spare time, although he had long stopped studying languages, and used them just for relaxation.
At the age of 12, Hamilton met and competed with mathematical savant
Savant syndrome
Savant syndrome , sometimes referred to as savantism, is a rare condition in which people with developmental disorders have one or more areas of expertise, ability, or brilliance that are in contrast with the individual's overall limitations...
Zerah Colburn
Zerah Colburn (math prodigy)
Zerah Colburn was a child prodigy of the 19th century who gained fame as a mental calculator.-Biography:He was born in Cabot, Vermont in 1804 and educated at Westminster School in London. He was thought to be mentally retarded until the age of seven. However, after six weeks of schooling his...
in mental arithmetic, whilst Colburn was in Dublin displaying his talents. Colburn more often than not came away the victor, which impressed Hamilton who was not used to being beaten in any contest of intellect. Hamilton was part of a small but well-regarded school of mathematicians associated with Trinity College, Dublin
Trinity College, Dublin
Trinity College, Dublin , formally known as the College of the Holy and Undivided Trinity of Queen Elizabeth near Dublin, was founded in 1592 by letters patent from Queen Elizabeth I as the "mother of a university", Extracts from Letters Patent of Elizabeth I, 1592: "...we...found and...
, which he entered at age 18 and where he spent his life. He studied both classics and science, and was appointed Professor of Astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
in 1827, prior to his graduation.
Optics and mechanics
Hamilton made important contributions to opticsOptics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
and to classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. His first discovery was in an early paper that he communicated in 1823 to Dr. Brinkley, who presented it under the title of "Caustics" in 1824 to the Royal Irish Academy
Royal Irish Academy
The Royal Irish Academy , based in Dublin, is an all-Ireland, independent, academic body that promotes study and excellence in the sciences, humanities and social sciences. It is one of Ireland's premier learned societies and cultural institutions and currently has around 420 Members, elected in...
. It was referred as usual to a committee. While their report acknowledged its novelty and value, they recommended further development and simplification before publication. Between 1825 to 1828 the paper grew to an immense size, mostly by the additional details which the committee had suggested. But it also became more intelligible, and the features of the new method were now easily to be seen. Until this period Hamilton himself seems not to have fully understood either the nature or importance of optics, as later he intended to apply his method to dynamics.
In 1827, Hamilton presented a theory of a single function, now known as Hamilton's principal function, that brings together mechanics, optics, and mathematics, and which helped to establish the wave theory of light. He proposed for it when he first predicted its existence in the third supplement to his "Systems of Rays", read in 1832. The Royal Irish Academy paper was finally entitled “Theory of Systems of Rays,” (23 April 1827) and the first part was printed in 1828 in the Transactions of the Royal Irish Academy. The more important contents of the second and third parts appeared in the three voluminous supplements (to the first part) which were published in the same Transactions, and in the two papers “On a General Method in Dynamics,” which appeared in the Philosophical Transactions in 1834 and 1835. In these papers, Hamilton developed his great principle of “Varying Action“. The most remarkable result of this work is the prediction that a single ray of light entering a biaxial crystal at a certain angle would emerge as a hollow cone of rays. This discovery is still known by its original name, "conical refraction".
The step from optics to dynamics in the application of the method of “Varying Action” was made in 1827, and communicated to the Royal Society, in whose Philosophical Transactions for 1834 and 1835 there are two papers on the subject, which, like the “Systems of Rays,” display a mastery over symbols and a flow of mathematical language almost unequaled. The common thread running through all this work is Hamilton's principle of “Varying Action“. Although it is based on the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
and may be said to belong to the general class of problems included under the principle of least action
Principle of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
which had been studied earlier by Pierre Louis Maupertuis
Maupertuis
Maupertuis may refer to:*Pierre Louis Maupertuis , a French mathematician and philosopher*Maupertuis, Manche, a commune in Manche, France*Maleperduis , the castle of Reynard in the Reynard cycle*Maupertus-sur-Mer, a commune in Manche, France...
, Euler, Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
, and others, Hamilton's analysis revealed much deeper mathematical structure than had been previously understood, in particular the symmetry between momentum and position. Paradoxically, the credit for discovering the quantity now called the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
and Lagrange's equations belongs to Hamilton. Hamilton's advances enlarged greatly the class of mechanical problems that could be solved, and they represent perhaps the greatest addition which dynamics
Analytical dynamics
In classical mechanics, analytical dynamics, or more briefly dynamics, is concerned about the relationship between motion of bodies and its causes, namely the forces acting on the bodies and the properties of the bodies...
had received since the work of Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Lagrange
Lagrange
La Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...
. Many scientists, including Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
, Jacobi, Darboux
Jean Gaston Darboux
Jean-Gaston Darboux was a French mathematician.-Life:Darboux made several important contributions to geometry and mathematical analysis . He was a biographer of Henri Poincaré and he edited the Selected Works of Joseph Fourier.Darboux received his Ph.D...
, Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, Kolmogorov, and Arnold, have extended Hamilton's work, thereby expanding our knowledge of mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
and differential equations.
While Hamilton's reformulation of classical mechanics is based on the same physical principles as the mechanics of Newton and Lagrange, it provides a powerful new technique for working with the equations of motion. More importantly, both the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
and Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
approaches which were initially developed to describe the motion of discrete system
Discrete system
A discrete system is a system with a countable number of states. Discrete systems may be contrasted with continuous systems, which may also be called analog systems. A final discrete system is often modeled with a directed graph and is analyzed for correctness and complexity according to...
s, have proven critical to the study of continuous classical systems in physics, and even quantum mechanical systems. In this way, the techniques find use in electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, quantum
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
relativity theory, and quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
Mathematical studies
Hamilton's mathematicalMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
studies seem to have been undertaken and carried to their full development without any assistance whatsoever, and the result is that his writings do not belong to any particular "school". Not only was Hamilton an expert as an arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
calculator, but he seems to have occasionally had fun in working out the result of some calculation to an enormous number of decimal places. At the age of twelve Hamilton engaged Zerah Colburn
Zerah Colburn (math prodigy)
Zerah Colburn was a child prodigy of the 19th century who gained fame as a mental calculator.-Biography:He was born in Cabot, Vermont in 1804 and educated at Westminster School in London. He was thought to be mentally retarded until the age of seven. However, after six weeks of schooling his...
, the American
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
"calculating boy
Mental calculator
Mental calculators are people with a prodigious ability in some area of mental calculation, such as multiplying large numbers or factoring large numbers...
", who was then being exhibited as a curiosity in Dublin, and did not always lose. Two years before, he had stumbled into a Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
copy of Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
, which he eagerly devoured; and at twelve Hamilton studied Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
’s Arithmetica Universalis
Arithmetica Universalis
100px|thumb|Title page of the Arithmetica, published 1707100px|thumb|The English translation by Raphson was published in 1720Arithmetica Universalis is a mathematics text by Isaac Newton. Written in Latin, it was edited and published by William Whiston, Newton's successor as Lucasian Professor of...
. This was his introduction to modern analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
. Hamilton soon began to read the Principia
Philosophiae Naturalis Principia Mathematica
Philosophiæ Naturalis Principia Mathematica, Latin for "Mathematical Principles of Natural Philosophy", often referred to as simply the Principia, is a work in three books by Sir Isaac Newton, first published 5 July 1687. Newton also published two further editions, in 1713 and 1726...
, and at sixteen Hamilton had mastered a great part of it, as well as some more modern works on analytical geometry and the differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
.
Around this time Hamilton was also preparing to enter Trinity College
Trinity College, Dublin
Trinity College, Dublin , formally known as the College of the Holy and Undivided Trinity of Queen Elizabeth near Dublin, was founded in 1592 by letters patent from Queen Elizabeth I as the "mother of a university", Extracts from Letters Patent of Elizabeth I, 1592: "...we...found and...
, Dublin, and therefore had to devote some time to classics. In mid-1822 he began a systematic study of Laplace's Mécanique Céleste
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
.
From that time Hamilton appears to have devoted himself almost wholly to mathematics, though he always kept himself well acquainted with the progress of science
History of science and technology
The history of science and technology is a field of history which examines how humanity's understanding of the natural world and ability to manipulate it have changed over the centuries...
both in Britain and abroad. Hamilton found an important defect in one of Laplace’s demonstrations, and he was induced by a friend to write out his remarks, so that they could be shown to Dr. John Brinkley
John Brinkley (astronomer)
The Rt. Rev. John Mortimer Brinkley D.D. was the first Royal Astronomer of Ireland and later Bishop of Cloyne.-Early years:...
, then the first Astronomer Royal for Ireland
Astronomer Royal for Ireland
The Royal Astronomer of Ireland was a title attached to the Andrews Professorship of astronomy in Trinity College Dublin and the directorship of its astronomical observatory at Dunsink, near Dublin. The eight title-holders included Charles Jasper Joly, Professor Sir Robert Stawell Ball, Professor...
, and an accomplished mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
. Brinkley seems to have immediately perceived Hamilton's talents, and to have encouraged him in the kindest way.
Hamilton’s career at College was perhaps unexampled. Amongst a number of extraordinary competitors, he was first in every subject and at every examination. He achieved the rare distinction of obtaining an optime both for Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
and for physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. Hamilton might have attained many more such honours (he was expected to win both the gold medal
Gold medal
A gold medal is typically the medal awarded for highest achievement in a non-military field. Its name derives from the use of at least a fraction of gold in form of plating or alloying in its manufacture...
s at the degree examination), if his career as a student had not been cut short by an unprecedented event. This was Hamilton’s appointment to the Andrews Professorship of Astronomy in the University of Dublin
University of Dublin
The University of Dublin , corporately designated the Chancellor, Doctors and Masters of the University of Dublin , located in Dublin, Ireland, was effectively founded when in 1592 Queen Elizabeth I issued a charter for Trinity College, Dublin, as "the mother of a university" – this date making it...
, vacated by Dr. Brinkley in 1827. The chair was not exactly offered to him, as has been sometimes asserted, but the electors, having met and talked over the subject, authorized Hamilton's personal friend (also an elector) to urge Hamilton to become a candidate, a step which Hamilton's modesty had prevented him from taking. Thus, when barely 22, Hamilton was established at the Dunsink Observatory
Dunsink Observatory
The Dunsink Observatory is an astronomical observatory established in 1785 in the townland of Dunsink near the city of Dublin, Ireland.Its most famous director was William Rowan Hamilton, who, amongst other things, discovered quaternions, the first non-commutative algebra, while strolling from the...
, near Dublin.
Hamilton was not especially suited for the post, because although he had a profound acquaintance with theoretical astronomy
Theoretical astronomy
Based on strict dictionary definitions, "astronomy" refers to "the study of objects and matter outside the Earth's atmosphere and of their physical and chemical properties" In some cases, as in the introduction of the introductory textbook The Physical Universe by Frank Shu, "astronomy" may be used...
, he had paid little attention to the regular work of the practical astronomer
Astronomer
An astronomer is a scientist who studies celestial bodies such as planets, stars and galaxies.Historically, astronomy was more concerned with the classification and description of phenomena in the sky, while astrophysics attempted to explain these phenomena and the differences between them using...
. Hamilton’s time was better employed in original investigations than it would have been spent in observations made even with the best of instruments. Hamilton was intended by the university authorities who elected him to the professorship of astronomy to spend his time as he best could for the advancement of science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
, without being tied down to any particular branch. If Hamilton had devoted himself to practical astronomy, the University of Dublin would assuredly have furnished him with instruments and an adequate staff of assistants.
In 1835, being secretary to the meeting of the British Association
British Association for the Advancement of Science
frame|right|"The BA" logoThe British Association for the Advancement of Science or the British Science Association, formerly known as the BA, is a learned society with the object of promoting science, directing general attention to scientific matters, and facilitating interaction between...
which was held that year in Dublin, he was knight
Knight
A knight was a member of a class of lower nobility in the High Middle Ages.By the Late Middle Ages, the rank had become associated with the ideals of chivalry, a code of conduct for the perfect courtly Christian warrior....
ed by the lord-lieutenant
Lord Lieutenant of Ireland
The Lord Lieutenant of Ireland was the British King's representative and head of the Irish executive during the Lordship of Ireland , the Kingdom of Ireland and the United Kingdom of Great Britain and Ireland...
. Other honours rapidly succeeded, among which his election in 1837 to the president
President
A president is a leader of an organization, company, trade union, university, or country.Etymologically, a president is one who presides, who sits in leadership...
’s chair in the Royal Irish Academy
Royal Irish Academy
The Royal Irish Academy , based in Dublin, is an all-Ireland, independent, academic body that promotes study and excellence in the sciences, humanities and social sciences. It is one of Ireland's premier learned societies and cultural institutions and currently has around 420 Members, elected in...
, and the rare distinction of being made a corresponding member of the Saint Petersburg Academy of Sciences. Later, in 1864, the newly established United States National Academy of Sciences
United States National Academy of Sciences
The National Academy of Sciences is a corporation in the United States whose members serve pro bono as "advisers to the nation on science, engineering, and medicine." As a national academy, new members of the organization are elected annually by current members, based on their distinguished and...
elected its first Foreign Associates, and decided to put Hamilton's name on top of their list.
Quaternions
The other great contribution Hamilton made to mathematical science was his discovery of quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s in 1843. However, in 1840, Benjamin Olinde Rodrigues had already reached a result that amounted to their discovery in all but name.
Hamilton was looking for ways of extending complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s (which can be viewed as points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
on a 2-dimensional plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
) to higher spatial dimensions.
He failed to find a useful 3-dimensional system (in modern terminology, he failed to find a real, three dimensional skew-field), but in working with four dimensions he created quaternions. According to Hamilton, on 16 October he was out walking along the Royal Canal in Dublin with his wife when the solution in the form of the equation
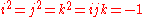
suddenly occurred to him; Hamilton then promptly carved this equation using his penknife into the side of the nearby Broom Bridge
Broom Bridge
Broom Bridge, also known as Brougham Bridge, is a bridge along Broombridge Road which crosses the Royal Canal in Cabra, Dublin, Ireland. Broom Bridge is named after William Brougham, one of the directors of the Royal Canal company...
(which Hamilton called Brougham Bridge), for fear he would forget it. This event marks the discovery of the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
.
A plaque under the bridge, was unveiled by the Taoiseach Éamon de Valera
Éamon de Valera
Éamon de Valera was one of the dominant political figures in twentieth century Ireland, serving as head of government of the Irish Free State and head of government and head of state of Ireland...
(himself a mathematician and student of quaternions), on November 13, 1958.
Since 1989, the National University of Ireland, Maynooth
National University of Ireland, Maynooth
The National University of Ireland, Maynooth , was founded by the Universities Act, 1997 as a constituent university of the National University of Ireland. It is Ireland's second oldest university, having been formed from St Patrick's College, Maynooth, itself founded in 1795.The university is...
has organized a pilgrimage, where mathematicians take a walk from Dunsink Observatory to the bridge, where no trace of the carving remains, though a stone plaque does commemorate the discovery.
The quaternion involved abandoning commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, a radical step for the time. Not only this, but Hamilton had in a sense invented the cross and dot products of vector algebra. Hamilton also described a quaternion as an ordered four-element multiple of real numbers, and described the first element as the 'scalar' part, and the remaining three as the 'vector' part.
Hamilton introduced, as a method of analysis, both quaternions and biquaternions, the extension to eight dimensions by introduction of complex number coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s. When his work was assembled in 1853, the book Lectures on Quaternions had "formed the subject of successive courses of lectures, delivered in 1848 and subsequent years, in the Halls of Trinity College, Dublin". Hamilton confidently declared that quaternions would be found to have a powerful influence as an instrument of research.
When he died, Hamilton was working on a definitive statement of quaternion science. His son William Edwin Hamilton brought the Elements of Quaternions, a hefty volume of 762 pages, to publication in 1866. As copies ran short, a second edition was prepared by Charles Jasper Joly
Charles Jasper Joly
Charles Jasper Joly was an Irish mathematician and astronomer who became Royal Astronomer of Ireland.-Life:...
, when the book was split into two volumes, the first appearing 1899 and the second in 1901. The subject index and footnotes in this second edition improved the Elements accessibility.
Peter Guthrie Tait
Peter Guthrie Tait
Peter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...
among others, advocated the use of Hamilton's quaternions. They were made a mandatory examination topic in Dublin, and for a while they were the only advanced mathematics taught in some American
universities. However, controversy about the use of quaternions grew in the late 19th century. Some of Hamilton's supporters vociferously opposed the growing fields of vector algebra and vector calculus (from developers like Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
and Josiah Willard Gibbs
Josiah Willard Gibbs
Josiah Willard Gibbs was an American theoretical physicist, chemist, and mathematician. He devised much of the theoretical foundation for chemical thermodynamics as well as physical chemistry. As a mathematician, he invented vector analysis . Yale University awarded Gibbs the first American Ph.D...
), because quaternions provide superior notation. While this is undeniable for four dimensions, quaternions cannot be used with arbitrary dimensionality (though extensions like Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s can). Vector notation had largely replaced the "space-time" quaternions in science and engineering by the mid-20th century.
Today, the quaternions are in use by computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, and orbital mechanics, mainly for representing rotations/orientations. For example, it is common for spacecraft attitude-control systems to be commanded in terms of quaternions, which are also used to telemeter their current attitude. The rationale is that combining many quaternion transformations is more numerically stable than combining many matrix transformations. In pure mathematics, quaternions show up significantly as one of the four finite-dimensional normed division algebra
Normed division algebra
In mathematics, a normed division algebra A is a division algebra over the real or complex numbers which is also a normed vector space, with norm || · || satisfying the following property:\|xy\| = \|x\| \|y\| for all x and y in A....
s over the real numbers, with applications throughout algebra and geometry.
Other originality
Hamilton originally matured his ideas before putting pen to paper. The discoveries, papers, and treatises previously mentioned might well have formed the whole work of a long and laborious life. But not to speak of his enormous collection of books, full to overflowing with new and original matter, which have been handed over to Trinity College, DublinTrinity College, Dublin
Trinity College, Dublin , formally known as the College of the Holy and Undivided Trinity of Queen Elizabeth near Dublin, was founded in 1592 by letters patent from Queen Elizabeth I as the "mother of a university", Extracts from Letters Patent of Elizabeth I, 1592: "...we...found and...
, the previous mentioned works barely form the greater portion of what Hamilton has published. Hamilton developed the variational principle
Variational principle
A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
, which was reformulated later by Carl Gustav Jacob Jacobi. He also introduced the Icosian game
Icosian game
The icosian game is a mathematical game invented in 1857 by William Rowan Hamilton. The game's object is finding a Hamiltonian cycle along the edges of a dodecahedron such that every vertex is visited a single time, no edge is visited twice, and the ending point is the same as the starting point...
or Hamilton's puzzle which can be solved using the concept of a Hamiltonian path
Hamiltonian path
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle in an undirected graph that visits each vertex exactly once and also returns to the starting vertex...
.
Hamilton's extraordinary investigations connected with the solution of algebraic equations of the fifth degree
Degree (mathematics)
In mathematics, there are several meanings of degree depending on the subject.- Unit of angle :A degree , usually denoted by ° , is a measurement of a plane angle, representing 1⁄360 of a turn...
, and his examination of the results arrived at by N. H. Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
, G. B. Jerrard, and others in their researches on this subject, form another contribution to science. There is next Hamilton's paper on fluctuating functions, a subject which, since the time of Joseph Fourier
Joseph Fourier
Jean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
, has been of immense and ever increasing value in physical applications of mathematics. There is also the extremely ingenious invention of the hodograph
Hodograph
A hodograph is a diagram that gives a vectorial visual representation of the movement of a body or a fluid. It is the locus of one end of a variable vector, with the other end fixed. The position of any plotted data on such a diagram is proportional to the velocity of the moving particle. It is...
. Of his extensive investigations into the solutions (especially by numerical approximation) of certain classes of physical differential equations, only a few items have been published, at intervals, in the Philosophical Magazine
Philosophical Magazine
The Philosophical Magazine is one of the oldest scientific journals published in English. Initiated by Alexander Tilloch in 1798, in 1822 Richard Taylor became joint editor and it has been published continuously by Taylor & Francis ever since; it was the journal of choice for such luminaries as...
.
Besides all this, Hamilton was a voluminous correspondent. Often a single letter of Hamilton's occupied from fifty to a hundred or more closely written pages, all devoted to the minute consideration of every feature of some particular problem; for it was one of the peculiar characteristics of Hamilton's mind never to be satisfied with a general understanding of a question; Hamilton pursued the problem until he knew it in all its details. Hamilton was ever courteous and kind in answering applications for assistance in the study of his works, even when his compliance must have cost him much time. He was excessively precise and hard to please with reference to the final polish of his own works for publication; and it was probably for this reason that he published so little compared with the extent of his investigations.
Death and afterwards

Gout
Gout is a medical condition usually characterized by recurrent attacks of acute inflammatory arthritis—a red, tender, hot, swollen joint. The metatarsal-phalangeal joint at the base of the big toe is the most commonly affected . However, it may also present as tophi, kidney stones, or urate...
precipitated by excessive drinking and overeating. He is buried in Mount Jerome Cemetery
Mount Jerome Cemetery
Mount Jerome Cemetery is situated in Harold's Cross on the south side of Dublin, Ireland. Since its foundation in 1836, it has witnessed over 300,000 burials...
in Dublin.
Hamilton is recognized as one of Ireland's leading scientists and, as Ireland becomes more aware of its scientific heritage, he is increasingly celebrated. The Hamilton Institute is an applied mathematics research institute at NUI Maynooth
National University of Ireland, Maynooth
The National University of Ireland, Maynooth , was founded by the Universities Act, 1997 as a constituent university of the National University of Ireland. It is Ireland's second oldest university, having been formed from St Patrick's College, Maynooth, itself founded in 1795.The university is...
and the Royal Irish Academy
Royal Irish Academy
The Royal Irish Academy , based in Dublin, is an all-Ireland, independent, academic body that promotes study and excellence in the sciences, humanities and social sciences. It is one of Ireland's premier learned societies and cultural institutions and currently has around 420 Members, elected in...
holds an annual public Hamilton lecture at which Murray Gell-Mann
Murray Gell-Mann
Murray Gell-Mann is an American physicist and linguist who received the 1969 Nobel Prize in physics for his work on the theory of elementary particles...
, Frank Wilczek
Frank Wilczek
Frank Anthony Wilczek is a theoretical physicist from the United States and a Nobel laureate. He is currently the Herman Feshbach Professor of Physics at the Massachusetts Institute of Technology ....
, Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
, and Timothy Gowers have all spoken. The year 2005 was the 200th anniversary of Hamilton's birth and the Irish government designated that the Hamilton Year, celebrating Irish science. Trinity College Dublin marked the year by launching the Hamilton Mathematics Institute TCD.
A commemorative coin was issued by the Central Bank of Ireland in his honour.
Commemorations of Hamilton
- Hamilton's equations are a formulation of classical mechanics.
- Numerous other concepts and objects in mechanics, such as Hamilton's principleHamilton's principleIn physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
, Hamilton's principal function, and the Hamilton–Jacobi equationHamilton–Jacobi equationIn mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
, are named after Hamilton. - The Hamiltonian is the name of both a function (classical) and an operator (quantum) in physics, and, in a different sense, a term from graph theoryGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. - The RCSI Hamilton SocietyHamilton SocietyThe Hamilton Society is a student group at the Royal College of Surgeons in Ireland . It was set up in 2004 to cater for the activities of students not already covered by other clubs or societies at RCSI....
was founded in his name in 2004. - The algebra of quaternions is usually denoted by H, or in blackboard boldBlackboard boldBlackboard bold is a typeface style that is often used for certain symbols in mathematical texts, in which certain lines of the symbol are doubled. The symbols usually denote number sets...
by , in honour of Hamilton.
, in honour of Hamilton.
Quotations
- "Time is said to have only one dimension, and space to have three dimensions. ... The mathematical quaternion partakes of both these elements; in technical language it may be said to be 'time plus space', or 'space plus time': and in this sense it has, or at least involves a reference to, four dimensions. And how the One of Time, of Space the Three, Might in the Chain of Symbols girdled be."—William Rowan Hamilton (quoted in Robert Percival Graves' "Life of Sir William Rowan Hamilton" (3 volumes, 1882, 1885, 1889))
- "He used to carry on, long trains of algebraic and arithmetical calculations in his mind, during which he was unconscious of the earthly necessity of eating; we used to bring in a ‘snack’ and leave it in his study, but a brief nod of recognition of the intrusion of the chop or cutlet was often the only result, and his thoughts went on soaring upwards." — William Edwin Hamilton (his elder son)
External links
- MacTutor's Sir William Rowan Hamilton. School of Mathematics, University of St AndrewsUniversity of St AndrewsThe University of St Andrews, informally referred to as "St Andrews", is the oldest university in Scotland and the third oldest in the English-speaking world after Oxford and Cambridge. The university is situated in the town of St Andrews, Fife, on the east coast of Scotland. It was founded between...
. - Wilkins, David R., Sir William Rowan Hamilton. School of Mathematics, Trinity College, Dublin.
- Wolfram Research's William Rowan Hamilton
- Cheryl Haefner's Sir William Rowan Hamilton
- 1911 Britannica Hamilton
- Hamilton Trust
- The Hamilton year 2005 web site
- The Hamilton Mathematics Institute, TCD
- Hamilton Institute
- Hamilton biography
Publications
- Hamilton, William Rowan (Royal Astronomer Of Ireland), "Introductory Lecture on Astronomy". Dublin University Review and Quarterly Magazine Vol. I, Trinity College, January 1833.
- Hamilton, William Rowan, "Lectures on Quaternions". Royal Irish Academy, 1853.
- Hamilton (1866) Elements of Quaternions University of DublinUniversity of DublinThe University of Dublin , corporately designated the Chancellor, Doctors and Masters of the University of Dublin , located in Dublin, Ireland, was effectively founded when in 1592 Queen Elizabeth I issued a charter for Trinity College, Dublin, as "the mother of a university" – this date making it...
Press. Edited by William Edwin Hamilton, son of the deceased author. - Hamilton (1899) Elements of Quaternions volume I, (1901) volume II. Edited by Charles Jasper JolyCharles Jasper JolyCharles Jasper Joly was an Irish mathematician and astronomer who became Royal Astronomer of Ireland.-Life:...
; published by Longmans, Green & Co.. - David R. Wilkins's collection of Hamilton's Mathematical Papers.

