
Icosian Calculus
Encyclopedia
The Icosian Calculus is a non-commutative algebraic structure
discovered by the Irish mathematician William Rowan Hamilton
in 1856.
In modern terms, he gave a group presentation of the icosahedral rotation group by generators
and relations.
Hamilton’s discovery derived from his attempts to find an algebra of "triplets" or 3-tuples
that he believed would reflect the three Cartesian axes. The symbols of the Icosian Calculus can be equated to moves between vertices on a dodecahedron. Hamilton’s work in this area resulted indirectly in the terms Hamiltonian circuit and Hamiltonian path
in graph theory. He also invented the Icosian game
as a means of illustrating and popularising his discovery.
 The algebra is based on three symbols that are each roots of unity, in that repeated application of any of them yields the value 1 after a particular number of steps. They are:
The algebra is based on three symbols that are each roots of unity, in that repeated application of any of them yields the value 1 after a particular number of steps. They are:

Hamilton also gives one other relation between the symbols:
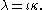
(In modern terms this is the (2,3,5) triangle group
.)
The operation is associative but not commutative. They generate a group of order 60, isomorphic to the group
of rotations of a regular icosahedron
or dodecahedron, and therefore to the alternating group of degree five.
Although the algebra exists as a purely abstract construction, it can be most easily visualised in terms of operations on the edges and vertices of a dodecahedron. Hamilton himself used a flattened dodecahedron as the basis for his instructional game.
Imagine an insect crawling along a particular edge of Hamilton's labelled dodecahedron in a certain direction, say from to
to  . We can represent this directed edge by
. We can represent this directed edge by  .
.
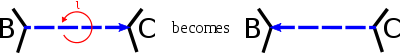
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
discovered by the Irish mathematician William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
in 1856.
In modern terms, he gave a group presentation of the icosahedral rotation group by generators
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
and relations.
Hamilton’s discovery derived from his attempts to find an algebra of "triplets" or 3-tuples
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
that he believed would reflect the three Cartesian axes. The symbols of the Icosian Calculus can be equated to moves between vertices on a dodecahedron. Hamilton’s work in this area resulted indirectly in the terms Hamiltonian circuit and Hamiltonian path
Hamiltonian path
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle in an undirected graph that visits each vertex exactly once and also returns to the starting vertex...
in graph theory. He also invented the Icosian game
Icosian game
The icosian game is a mathematical game invented in 1857 by William Rowan Hamilton. The game's object is finding a Hamiltonian cycle along the edges of a dodecahedron such that every vertex is visited a single time, no edge is visited twice, and the ending point is the same as the starting point...
as a means of illustrating and popularising his discovery.
Informal definition


Hamilton also gives one other relation between the symbols:
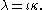
(In modern terms this is the (2,3,5) triangle group
Triangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
.)
The operation is associative but not commutative. They generate a group of order 60, isomorphic to the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of rotations of a regular icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
or dodecahedron, and therefore to the alternating group of degree five.
Although the algebra exists as a purely abstract construction, it can be most easily visualised in terms of operations on the edges and vertices of a dodecahedron. Hamilton himself used a flattened dodecahedron as the basis for his instructional game.
Imagine an insect crawling along a particular edge of Hamilton's labelled dodecahedron in a certain direction, say from
 to
to  . We can represent this directed edge by
. We can represent this directed edge by  .
.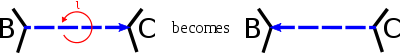
- The Icosian symbol
 equates to changing direction on any edge, so the insect crawls from
equates to changing direction on any edge, so the insect crawls from  to
to 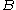 (following the directed edge
(following the directed edge 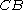 ).
).
- The Icosian symbol
 equates to rotating the insect's current travel anti-clockwise around the end point. In our example this would mean changing the initial direction
equates to rotating the insect's current travel anti-clockwise around the end point. In our example this would mean changing the initial direction  to become
to become 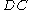 .
.
- The Icosian symbol
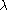 equates to making a right-turn at the end point, moving from
equates to making a right-turn at the end point, moving from  to
to  .
.
Legacy
The Icosian Calculus is one of the earliest examples of many mathematical ideas, including:- presenting and studying a group by generators and relations;
- a triangle groupTriangle groupIn mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
, later generalized to Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s; - visualization of a group by a graph, which led to combinatorial group theoryCombinatorial group theoryIn mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations...
and later geometric group theoryGeometric group theoryGeometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
; - Hamiltonian circuits and Hamiltonian pathHamiltonian pathIn the mathematical field of graph theory, a Hamiltonian path is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle in an undirected graph that visits each vertex exactly once and also returns to the starting vertex...
s in graph theory; - dessin d'enfantDessin d'enfantIn mathematics, a dessin d'enfant is a type of graph drawing used to study Riemann surfaces and to provide combinatorial invariants for the action of the absolute Galois group of the rational numbers.Intuitively, a dessin d'enfant is simply a graph, with its vertices colored alternating black and...
– see dessin d'enfant: history for details.

