Colin de Verdière graph invariant
Encyclopedia
Colin de Verdière's invariant is a graph parameter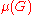 
for any graph
G introduced by Yves Colin de Verdière
in 1990. It was motivated by the study of the maximum multiplicity of the second eigenvalue of certain Schrödinger operators.
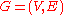be a loopless simple graph. Assume without loss of generality that 
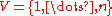. Then 
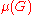is the largest corank of any matrix
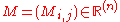such that:
; if and only if G is planar
; if and only if G is linklessly embeddable graph
These same families of graphs also show up in connections between the Colin de Verdière invariant of a graph and the structure of its complement graph
:
of a graph is another graph formed from it by contracting edges and by deleting edges and vertices. The Colin de Verdière invariant is minor-monotone, meaning that taking a minor of a graph can only decrease or leave unchanged its invariant:
By the Robertson–Seymour theorem
, for every k there exists a finite set H of graphs such that the graphs with invariant at most k are the same as the graphs that do not have any member of H as a minor. lists these sets of forbidden minors for k ≤ 3; for k = 4 the set of forbidden minors consists of the seven graphs in the Petersen family
, due to the two characterizations of the linklessly embeddable graph
s as the graphs with μ ≤ 4 and as the graphs with no Petersen family minor.
with at most μ + 1 colors. For instance, the linear forests have invariant 1, and can be 2-colored
; the outerplanar graph
s have invariant two, and can be 3-colored; the planar graph
s have invariant 3, and (by the four color theorem
) can be 4-colored.
For graphs with Colin de Verdière invariant at most four, the conjecture remains true; these are the linklessly embeddable graph
s, and the fact that they have chromatic number at most five is a consequence of a proof by of the Hadwiger conjecture
for K6-minor-free graphs.
k, it has Colin de Verdière invariant at most k + 3. For instance, the two Kuratowski graphs K5 and K3,3 can both be drawn with a single crossing, and have Colin de Verdière invariant at most four.
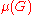for any graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
G introduced by Yves Colin de Verdière
Yves Colin de Verdière
Yves Colin de Verdière is a French mathematician.He studied at the ENS in the late 1960s, obtained his PhD in 1973, and then spent the bulk of his working life in Grenoble...
in 1990. It was motivated by the study of the maximum multiplicity of the second eigenvalue of certain Schrödinger operators.
Definition
Let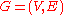 be a loopless simple graph. Assume without loss of generality that 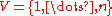. Then 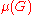is the largest corank of any matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
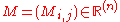such that:
- (M1) for all
with 
: 
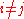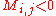if i and j are adjacent, and 
if i and j are nonadjacent; - (M2) M has exactly one negative eigenvalue, of multiplicity 1;
- (M3) there is no nonzero matrix
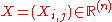such that 
and such that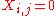 
whenever 
or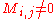 
.
Characterization of known graph families
Several well-known families of graphs can be characterized in terms of their Colin de Verdière invariants: if and only if G has no edges; if and only if G is a linear forest (disjoint union of paths); if and only if G is outerplanarOuterplanar graph
In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...
; if and only if G is planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
; if and only if G is linklessly embeddable graph
Linkless embedding
In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph have nonzero linking number. A flat embedding is an embedding with the property that every cycle is the...
These same families of graphs also show up in connections between the Colin de Verdière invariant of a graph and the structure of its complement graph
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
:
- If the complement of an n-vertex graph is a linear forest, then ;
- If the complement of an n-vertex graph is outerplanar, then ;
- If the complement of an n-vertex graph is planar, then .
Graph minors
A minorMinor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
of a graph is another graph formed from it by contracting edges and by deleting edges and vertices. The Colin de Verdière invariant is minor-monotone, meaning that taking a minor of a graph can only decrease or leave unchanged its invariant:
- If H is a minor of G then
.
By the Robertson–Seymour theorem
Robertson–Seymour theorem
In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering...
, for every k there exists a finite set H of graphs such that the graphs with invariant at most k are the same as the graphs that do not have any member of H as a minor. lists these sets of forbidden minors for k ≤ 3; for k = 4 the set of forbidden minors consists of the seven graphs in the Petersen family
Petersen family
In graph theory, the Petersen family is a set of seven undirected graphs that includes the Petersen graph and the complete graph K6. The Petersen family is named after Danish mathematician Julius Petersen, the namesake of the Petersen graph....
, due to the two characterizations of the linklessly embeddable graph
Linkless embedding
In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph have nonzero linking number. A flat embedding is an embedding with the property that every cycle is the...
s as the graphs with μ ≤ 4 and as the graphs with no Petersen family minor.
Chromatic number
conjectured that any graph with Colin de Verdière invariant μ may be coloredGraph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
with at most μ + 1 colors. For instance, the linear forests have invariant 1, and can be 2-colored
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
; the outerplanar graph
Outerplanar graph
In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...
s have invariant two, and can be 3-colored; the planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s have invariant 3, and (by the four color theorem
Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
) can be 4-colored.
For graphs with Colin de Verdière invariant at most four, the conjecture remains true; these are the linklessly embeddable graph
Linkless embedding
In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph have nonzero linking number. A flat embedding is an embedding with the property that every cycle is the...
s, and the fact that they have chromatic number at most five is a consequence of a proof by of the Hadwiger conjecture
Hadwiger conjecture (graph theory)
In graph theory, the Hadwiger conjecture states that, if all proper colorings of an undirected graph G use k or more colors, then one can find k disjoint connected subgraphs of G such that each subgraph is connected by an edge to each other subgraph...
for K6-minor-free graphs.
Other properties
If a graph has crossing numberCrossing number
Crossing number may refer to:*Crossing number of a knot is the minimal number of crossings in any knot diagram for the knot.**The average crossing number is a variant of crossing number obtained from a three-dimensional embedding of a knot by averaging over all two-dimensional...
k, it has Colin de Verdière invariant at most k + 3. For instance, the two Kuratowski graphs K5 and K3,3 can both be drawn with a single crossing, and have Colin de Verdière invariant at most four.