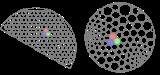
Circle packing theorem
Encyclopedia
The circle packing theorem (also known as the Koebe–Andreev–Thurston theorem) describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles (in general, on any Riemann surface) whose interiors are disjoint. The intersection graph
(sometimes called the tangency graph or contact graph) of a circle packing is the graph having a vertex
for each circle, and an edge for every pair of circles that are tangent
. If the circle packing is on the plane, or, equivalently, on the sphere, then its intersection graph is called a coin graph. Coin graphs are always connected, simple, and planar
. The circle packing theorem states that the converse also holds:
Circle packing theorem: For
every connected simple planar graph G there is a circle packing in the plane
whose intersection graph is (isomorphic
to) G.
planar and every connected component of the complement of the embedding of G in the sphere has precisely three edges on its boundary, or in other words, if G is the 1-skeleton of a simplicial complex
which is homeomorphic to the sphere. Any triangulated planar graph G is connected and simple, so the circle packing theorem guarantees the existence of a circle packing whose intersection graph is (isomorphic to) G. Such a G must also be finite, so its packing will have a finite number of circles. As the following theorem states more formally, every maximal planar graph can have at most one packing.
Koebe–Andreev–Thurston theorem: If G is a finite triangulated planar graph, then the circle packing whose tangency graph is (isomorphic to) G is unique, up to
Möbius transformations and reflections in lines.
Thurston observes that this uniqueness is a consequence of the Mostow rigidity theorem
. The plane in which the circles are packed may be viewed as the boundary of a halfspace model
for hyperbolic space
; with this view, each circle is the boundary of a plane within the hyperbolic space. One can define a set of disjoint planes from the circles of the packing, and a second set of disjoint planes defined by the circles surrounding each triangular gap between three of the circles in the packing. These two sets of planes meet at right angles, and form the generator
s of a reflection group
whose fundamental domain
can be viewed as a hyperbolic manifold
. By Mostow rigidity, the hyperbolic structure of this domain is uniquely determined, up to isometry
of the hyperbolic space; these isometries, when viewed in terms of their actions on the Euclidean plane on the boundary of the half-plane model, translate to Möbius transformations.
There is also a more elementary proof based on the maximum principle
and on the observation that, in the triangle connecting the centers of three mutually tangent circles, the
angle formed at the center of one of the circles is monotone decreasing in its radius and monotone increasing in the two other radii. Given two packings for the same graph G, one may apply reflections and Möbius transformations to make the outer circles in these two packings correspond to each other and have the same radii. Then, let v be an interior vertex of G for which the circles in the two packings have sizes that are as far apart as possible: that is, choose v to maximize the ratio r1/r2 of the radii of its circles in the two packings. For each triangular face of G containing v, it follows that the angle at the center of the circle for v in the first packing is less than or equal to the angle in the second packing, with equality possible only when the other two circles forming the triangle have the same ratio r1/r2 of radii in the two packings. But the sum of the angles of all of these triangles surrounding the center of the triangle must be 2π in both packings, so all neighboring vertices to v must have the same ratio as v itself. By applying the same argument to these other circles in turn, it follows that all circles in both packings have the same ratio. But the outer circles have been transformed to have ratio 1, so r1/r2 = 1 and the two packings have identical radii for all circles.
If G is a graph that can be embedded on a surface S,
then there is a constant curvature
Riemannian metric
d on S and a circle packing on (S, d) whose contacts graph is isomorphic to G. If S is closed (compact
and without boundary)
and G is a triangulation of S, then (S, d) and the packing are unique up to conformal equivalence. If S is the sphere, then this equivalence is up to Möbius transformations; if it is a torus, then the equivalence is up to scaling by a constant and isometries, while if S has genus
at least 2, then the equivalence is up to isometries.
Another generalization of the circle packing theorem involves replacing the condition of tangency with a specified intersection angle between circles corresponding to neighboring vertices. A particularly elegant version is as follows. Suppose that G is a finite 3-connected
planar graph (that is, a polyhedral graph
), then there is a pair of circle packings, one whose intersection graph is isomorphic to G, another whose intersection graph is isomorphic to the planar dual
of G,
and for every vertex in G and face adjacent to it, the circle in the first packing corresponding to the vertex
intersects orthogonally with the circle in the second packing corresponding to the face.
Yet another variety of generalizations allow shapes that are not circles.
Suppose that G = (V, E) is a finite planar graph, and to each vertex v of G
corresponds a shape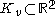
, which is homeomorphic
to the closed unit disk and whose boundary is smooth.
Then there is a packing
in the plane
such that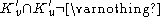
if and only if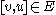 
and for each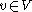
the set 
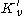is obtained from 
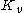by translating
and scaling. (Note that in the original circle packing theorem, there are three real parameters per vertex,
two of which describe the center of the corresponding circle and one of which describe the radius, and there is one equation per edge. This also holds in this generalization.)
One proof of this generalization can be obtained by applying Koebe's original proof and the theorem
of Brandt and Harrington stating that any finitely connected domain is conformally equivalent to
a planar domain whose boundary components have specified shapes, up to translations and scaling.
geometry, conformal mappings and planar graphs. An elegant proof of the planar separator theorem
,
originally due to Lipton and Tarjan, has been obtained in this way.
Another application of the circle packing theorem is that unbiased limits of
bounded-degree planar graphs are almost surely recurrent.
Other applications include implications for the cover time.
and estimates for the largest eigenvalue of bounded-genus
graphs.
Circle packing has also become an essential tool in origami
design, as each appendage on an origami figure requires a circle of paper. Robert J. Lang
has used the mathematics of circle packing to develop computer programs that aid in the design of complex origami figures.
's original proof is
based on his conformal uniformization theorem saying that a finitely connected planar domain
is conformally equivalent to a circle domain. There are several different topological proofs
that are known. Thurston's proof is based on Brouwer's fixed point theorem
.
There is also a proof using a discrete variant of Perron's method of constructing solutions to the
Dirichlet problem
. Yves Colin de Verdière
proved
the existence of the circle packing as a minimizer of a convex function
on a certain configuration
space.
, that every graph that can be drawn
without crossings in the plane using curved edges can also be drawn without crossings using straight line segment
edges, follows as a simple corollary of the circle packing theorem: by placing vertices at the centers of the circles and drawing straight edges between them, a straight-line planar embedding is obtained.
A variation of the circle packing theorem asserts that any polyhedral graph
and its dual graph
can be represented by two circle packings, such that the two tangent circles representing a primal graph edge and the two tangent circles representing the dual of the same edge always have their tangencies at right angles to each other at the same point of the plane. A packing of this type can be used to construct a convex polyhedron that represents the given graph and that has a midsphere
, a sphere tangent to all of the edges of the polyhedron. Conversely, if a polyhedron has a midsphere, then the circles formed by the intersections of the sphere with the polyhedron faces and the circles formed by the horizons on the sphere as viewed from each polyhedron vertex form a dual packing of this type.
. The version of the circle packing problem that they solve takes as input a planar graph, in which all the internal faces are triangles and for which the external vertices have been labeled by positive numbers. It produces as output a circle packing whose tangencies represent the given graph, and for which the circles representing the external vertices have the radii specified in the input. As they suggest, the key to the problem is to first calculate the radii of the circles in the packing; once the radii are known, the geometric positions of the circles are not difficult to calculate. They begin with a set of tentative radii that do not correspond to a valid packing, and then repeatedly perform the following steps:
Each of these steps may be performed with simple trigonometric calculations, and as Collins and Stephenson argue, the system of radii converges rapidly to a unique fixed point
for which all covering angles are exactly 2π. Once the system has converged, the circles may be placed one at a time, at each step using the positions and radii of two neighboring circles to determine the center of each successive circle.
describes a similar iterative technique for finding simultaneous packings of a polyhedral graph
and its dual, in which the dual circles are at right angles to the primal circles. He proves that the method takes time polynomial in the number of circles and in log 1/ε, where ε is a bound on the distance of the centers and radii of the computed packing from those in an optimal packing.
.
William Thurston
rediscovered the circle packing theorem, and
noted that it followed from the work of E. M. Andreev. Thurston also proposed a scheme for using the circle packing theorem to obtain a homeomorphism of a simply connected proper subset of the plane onto the interior of the unit disk. The Thurston Conjecture for Circle Packings is his conjecture that the homeomorphism will converge to the Riemann mapping as the radii of the circles tend to zero. The Thurston Conjecture was later proved
by Burton Rodin
and Dennis Sullivan
.
This led to a flurry of research on extensions of the circle packing theorem, relations to
conformal mappings, and applications.
Intersection graph
In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...
(sometimes called the tangency graph or contact graph) of a circle packing is the graph having a vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
for each circle, and an edge for every pair of circles that are tangent
Tangent circles
In geometry, tangent circles are circles in a common plane that intersect in a single point. There are two types of tangency: internal and external...
. If the circle packing is on the plane, or, equivalently, on the sphere, then its intersection graph is called a coin graph. Coin graphs are always connected, simple, and planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
. The circle packing theorem states that the converse also holds:
Circle packing theorem: For
every connected simple planar graph G there is a circle packing in the plane
whose intersection graph is (isomorphic
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
to) G.
A uniqueness statement
A graph G is triangulated planar if it isplanar and every connected component of the complement of the embedding of G in the sphere has precisely three edges on its boundary, or in other words, if G is the 1-skeleton of a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
which is homeomorphic to the sphere. Any triangulated planar graph G is connected and simple, so the circle packing theorem guarantees the existence of a circle packing whose intersection graph is (isomorphic to) G. Such a G must also be finite, so its packing will have a finite number of circles. As the following theorem states more formally, every maximal planar graph can have at most one packing.
Koebe–Andreev–Thurston theorem: If G is a finite triangulated planar graph, then the circle packing whose tangency graph is (isomorphic to) G is unique, up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
Möbius transformations and reflections in lines.
Thurston observes that this uniqueness is a consequence of the Mostow rigidity theorem
Mostow rigidity theorem
In mathematics, Mostow's rigidity theorem, or strong rigidity theorem, or Mostow–Prasad rigidity theorem, essentially states that the geometry of a finite-volume hyperbolic manifold of dimension greater than two is determined by the fundamental group and hence unique...
. The plane in which the circles are packed may be viewed as the boundary of a halfspace model
Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
for hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
; with this view, each circle is the boundary of a plane within the hyperbolic space. One can define a set of disjoint planes from the circles of the packing, and a second set of disjoint planes defined by the circles surrounding each triangular gap between three of the circles in the packing. These two sets of planes meet at right angles, and form the generator
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
s of a reflection group
Reflection group
In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...
whose fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
can be viewed as a hyperbolic manifold
Hyperbolic manifold
In mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...
. By Mostow rigidity, the hyperbolic structure of this domain is uniquely determined, up to isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of the hyperbolic space; these isometries, when viewed in terms of their actions on the Euclidean plane on the boundary of the half-plane model, translate to Möbius transformations.
There is also a more elementary proof based on the maximum principle
Maximum principle
In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
and on the observation that, in the triangle connecting the centers of three mutually tangent circles, the
angle formed at the center of one of the circles is monotone decreasing in its radius and monotone increasing in the two other radii. Given two packings for the same graph G, one may apply reflections and Möbius transformations to make the outer circles in these two packings correspond to each other and have the same radii. Then, let v be an interior vertex of G for which the circles in the two packings have sizes that are as far apart as possible: that is, choose v to maximize the ratio r1/r2 of the radii of its circles in the two packings. For each triangular face of G containing v, it follows that the angle at the center of the circle for v in the first packing is less than or equal to the angle in the second packing, with equality possible only when the other two circles forming the triangle have the same ratio r1/r2 of radii in the two packings. But the sum of the angles of all of these triangles surrounding the center of the triangle must be 2π in both packings, so all neighboring vertices to v must have the same ratio as v itself. By applying the same argument to these other circles in turn, it follows that all circles in both packings have the same ratio. But the outer circles have been transformed to have ratio 1, so r1/r2 = 1 and the two packings have identical radii for all circles.
Generalizations of the circle packing theorem
The circle packing theorem generalizes to graphs that are not planar.If G is a graph that can be embedded on a surface S,
then there is a constant curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
Riemannian metric
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
d on S and a circle packing on (S, d) whose contacts graph is isomorphic to G. If S is closed (compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and without boundary)
and G is a triangulation of S, then (S, d) and the packing are unique up to conformal equivalence. If S is the sphere, then this equivalence is up to Möbius transformations; if it is a torus, then the equivalence is up to scaling by a constant and isometries, while if S has genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
at least 2, then the equivalence is up to isometries.
Another generalization of the circle packing theorem involves replacing the condition of tangency with a specified intersection angle between circles corresponding to neighboring vertices. A particularly elegant version is as follows. Suppose that G is a finite 3-connected
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
planar graph (that is, a polyhedral graph
Polyhedral graph
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
), then there is a pair of circle packings, one whose intersection graph is isomorphic to G, another whose intersection graph is isomorphic to the planar dual
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
of G,
and for every vertex in G and face adjacent to it, the circle in the first packing corresponding to the vertex
intersects orthogonally with the circle in the second packing corresponding to the face.
Yet another variety of generalizations allow shapes that are not circles.
Suppose that G = (V, E) is a finite planar graph, and to each vertex v of G
corresponds a shape
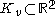, which is homeomorphicHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to the closed unit disk and whose boundary is smooth.
Then there is a packing
in the planesuch that
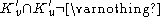if and only if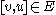 and for each
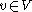the set 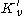is obtained from 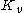by translatingand scaling. (Note that in the original circle packing theorem, there are three real parameters per vertex,
two of which describe the center of the corresponding circle and one of which describe the radius, and there is one equation per edge. This also holds in this generalization.)
One proof of this generalization can be obtained by applying Koebe's original proof and the theorem
of Brandt and Harrington stating that any finitely connected domain is conformally equivalent to
a planar domain whose boundary components have specified shapes, up to translations and scaling.
Relations with conformal mapping theory
Applications of the circle packing theorem
The circle packing theorem is a useful tool to study various problems in planargeometry, conformal mappings and planar graphs. An elegant proof of the planar separator theorem
Planar separator theorem
In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices...
,
originally due to Lipton and Tarjan, has been obtained in this way.
Another application of the circle packing theorem is that unbiased limits of
bounded-degree planar graphs are almost surely recurrent.
Other applications include implications for the cover time.
and estimates for the largest eigenvalue of bounded-genus
Genus
In biology, a genus is a low-level taxonomic rank used in the biological classification of living and fossil organisms, which is an example of definition by genus and differentia...
graphs.
Circle packing has also become an essential tool in origami
Origami
is the traditional Japanese art of paper folding, which started in the 17th century AD at the latest and was popularized outside Japan in the mid-1900s. It has since then evolved into a modern art form...
design, as each appendage on an origami figure requires a circle of paper. Robert J. Lang
Robert J. Lang
Dr. Robert J. Lang is an American physicist who is also one of the foremost origami artists and theorists in the world. He is known for his complex and elegant designs, most notably of insects and animals. He has long been a student of the mathematics of origami and of using computers to study the...
has used the mathematics of circle packing to develop computer programs that aid in the design of complex origami figures.
Proofs of the theorem
There are many known proofs of the circle packing theorem. Paul KoebePaul Koebe
Paul Koebe was a 20th-century German mathematician. His work dealt exclusively with the complex numbers, his most important results being on the uniformization of Riemann surfaces in a series of four papers in 1907–1909. He did his thesis at Berlin, where he worked under Herman Schwarz...
's original proof is
based on his conformal uniformization theorem saying that a finitely connected planar domain
is conformally equivalent to a circle domain. There are several different topological proofs
that are known. Thurston's proof is based on Brouwer's fixed point theorem
Brouwer fixed point theorem
Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
.
There is also a proof using a discrete variant of Perron's method of constructing solutions to the
Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
. Yves Colin de Verdière
Yves Colin de Verdière
Yves Colin de Verdière is a French mathematician.He studied at the ENS in the late 1960s, obtained his PhD in 1973, and then spent the bulk of his working life in Grenoble...
proved
the existence of the circle packing as a minimizer of a convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
on a certain configuration
space.
Implications
Fáry's theoremFáry's theorem
In mathematics, Fáry's theorem states that any simple planar graph can be drawn without crossings so that its edges are straight line segments. That is, the ability to draw graph edges as curves instead of as straight line segments does not allow a larger class of graphs to be drawn...
, that every graph that can be drawn
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
without crossings in the plane using curved edges can also be drawn without crossings using straight line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
edges, follows as a simple corollary of the circle packing theorem: by placing vertices at the centers of the circles and drawing straight edges between them, a straight-line planar embedding is obtained.
A variation of the circle packing theorem asserts that any polyhedral graph
Polyhedral graph
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
and its dual graph
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
can be represented by two circle packings, such that the two tangent circles representing a primal graph edge and the two tangent circles representing the dual of the same edge always have their tangencies at right angles to each other at the same point of the plane. A packing of this type can be used to construct a convex polyhedron that represents the given graph and that has a midsphere
Midsphere
In geometry, the midsphere or intersphere of a polyhedron is a sphere which is tangent to every edge of the polyhedron. That is to say, it touches any given edge at exactly one point...
, a sphere tangent to all of the edges of the polyhedron. Conversely, if a polyhedron has a midsphere, then the circles formed by the intersections of the sphere with the polyhedron faces and the circles formed by the horizons on the sphere as viewed from each polyhedron vertex form a dual packing of this type.
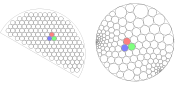
Algorithmic aspects
describe a numerical relaxation algorithm for finding circle packings, based on ideas of William ThurstonWilliam Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
. The version of the circle packing problem that they solve takes as input a planar graph, in which all the internal faces are triangles and for which the external vertices have been labeled by positive numbers. It produces as output a circle packing whose tangencies represent the given graph, and for which the circles representing the external vertices have the radii specified in the input. As they suggest, the key to the problem is to first calculate the radii of the circles in the packing; once the radii are known, the geometric positions of the circles are not difficult to calculate. They begin with a set of tentative radii that do not correspond to a valid packing, and then repeatedly perform the following steps:
- Choose an internal vertex v of the input graph.
- Calculate the total angle θ that its k neighboring circles would cover around the circle for v, if the neighbors were placed tangent to each other and to the central circle using their tentative radii.
- Determine a representative radius r for the neighboring circles, such that k circles of radius r would give the same covering angle θ as the neighbors of v give.
- Set the new radius for v to be the value for which k circles of radius r would give a covering angle of exactly 2π.
Each of these steps may be performed with simple trigonometric calculations, and as Collins and Stephenson argue, the system of radii converges rapidly to a unique fixed point
Fixed point
"Fixed point" has many meanings in science, most of them mathematical.* Fixed point * Fixed-point combinator* Fixed-point arithmetic, a manner of doing arithmetic on computers* Benchmark , fixed points used by geodesists...
for which all covering angles are exactly 2π. Once the system has converged, the circles may be placed one at a time, at each step using the positions and radii of two neighboring circles to determine the center of each successive circle.
describes a similar iterative technique for finding simultaneous packings of a polyhedral graph
Polyhedral graph
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
and its dual, in which the dual circles are at right angles to the primal circles. He proves that the method takes time polynomial in the number of circles and in log 1/ε, where ε is a bound on the distance of the centers and radii of the computed packing from those in an optimal packing.
History
The circle packing theorem was first proved by Paul KoebePaul Koebe
Paul Koebe was a 20th-century German mathematician. His work dealt exclusively with the complex numbers, his most important results being on the uniformization of Riemann surfaces in a series of four papers in 1907–1909. He did his thesis at Berlin, where he worked under Herman Schwarz...
.
William Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
rediscovered the circle packing theorem, and
noted that it followed from the work of E. M. Andreev. Thurston also proposed a scheme for using the circle packing theorem to obtain a homeomorphism of a simply connected proper subset of the plane onto the interior of the unit disk. The Thurston Conjecture for Circle Packings is his conjecture that the homeomorphism will converge to the Riemann mapping as the radii of the circles tend to zero. The Thurston Conjecture was later proved
by Burton Rodin
Burton Rodin
Burt Rodin is an American mathematician known for his research in conformal mapping and Riemann surfaces. He was a professor at the University of California, San Diego 1970–1994 where he was Chair of the Mathematics Department 1977–1981. He became Professor Emeritus in June 1994.He...
and Dennis Sullivan
Dennis Sullivan
Dennis Parnell Sullivan is an American mathematician. He is known for work in topology, both algebraic and geometric, and on dynamical systems. He holds the Albert Einstein Chair at the City University of New York Graduate Center, and is a professor at Stony Brook University.-Work in topology:He...
.
This led to a flurry of research on extensions of the circle packing theorem, relations to
conformal mappings, and applications.
See also
- Packing problemPacking problemPacking problems are a class of optimization problems in mathematics which involve attempting to pack objects together , as densely as possible. Many of these problems can be related to real life packaging, storage and transportation issues...
- Sphere packingSphere packingIn geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
- Apollonian networkApollonian networkIn combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable...
, a type of planar graph defined from a circle packing
External links
- CirclePack (free software for constructing circle packings from graphs) and Circle packing bibliography by Kenneth Stephenson, Univ. of Tennessee