
Quartic surface
Encyclopedia
In mathematics, especially in algebraic geometry
, a quartic surface is a surface defined by an equation of degree 4.
More specifically there are two closely related types of quartic surface: affine and projective. An affine quartic surface is the solution set of an equation of the form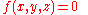
where f is a polynomial of degree 4, such as f(x,y,z) = x4 + y4 + xyz + z2 − 1. This is a surface in affine space
.
On the other hand, a projective quartic surface is a surface in projective space
P3 of the same form, but now f is a homogeneous polynomial of 4 variables of degree 4, so for example f(x,y,z,w) = x4 + y4 + xyzw + z2w2 − w4.
If the base field in R or C the surface is said to be real or complex. If on the other hand the base field is finite, then it is said to be an arithmetic quartic surface.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a quartic surface is a surface defined by an equation of degree 4.
More specifically there are two closely related types of quartic surface: affine and projective. An affine quartic surface is the solution set of an equation of the form
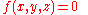
where f is a polynomial of degree 4, such as f(x,y,z) = x4 + y4 + xyz + z2 − 1. This is a surface in affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
.
On the other hand, a projective quartic surface is a surface in projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
P3 of the same form, but now f is a homogeneous polynomial of 4 variables of degree 4, so for example f(x,y,z,w) = x4 + y4 + xyzw + z2w2 − w4.
If the base field in R or C the surface is said to be real or complex. If on the other hand the base field is finite, then it is said to be an arithmetic quartic surface.
Special quartic surfaces
- Dupin cyclides
- The Fermat quartic, given by x4 + y4 + z4 + w4 =0 (an example of a K3 surface) – and tiled by 12 octagons, in the Dyck tiling (named after Walther von DyckWalther von DyckWalther Franz Anton von Dyck , born Dyck and later ennobled, was a German mathematician...
). - K3 surfaceK3 surfaceIn mathematics, a K3 surface is a complex or algebraic smooth minimal complete surface that is regular and has trivial canonical bundle.In the Enriques-Kodaira classification of surfaces they form one of the 5 classes of surfaces of Kodaira dimension 0....
s - Klein quarticKlein quarticIn hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
- Kummer surface
- Plücker surfacePlücker surfaceIn algebraic geometry, a Plücker surface, studied by , is a quartic surface in 3-dimensional projective space with a double line and 8 nodes.-Construction:For any quadric line complex, the lines of the complex in a plane envelop a quadric in the plane...
- Weddle surfaceWeddle surfaceIn algebraic geometry, a Weddle surface is a quartic surface in 3-dimensional projective space, given by the locus of vertices of the 3-dimensional family of cones passing through 6 points in general position, and studied by ....
See also
- Quadric surface (The union of two quadric surfaces is a special case of a quartic surface)
- Cubic surfaceCubic surfaceA cubic surface is a projective variety studied in algebraic geometry. It is an algebraic surface in three-dimensional projective space defined by a single polynomial which is homogeneous of degree 3...
(The union of a cubic surface and a plane is another particular type of quartic surface)

