Character sum
Encyclopedia
In mathematics
, a character sum is a sum
of values of a Dirichlet character
χ modulo
N, taken over a given range of values of n. Such sums are basic in a number of questions, for example in the distribution of quadratic residues, and in particular in the classical question of finding an upper bound for the least quadratic nonresidue modulo N. Character sums are often closely linked to exponential sum
s by the Gauss sum
s (this is like a finite Mellin transform
.)
Assume χ is a nonprincipal Dirichlet character to the modulus N.
over relatively short ranges, of length R < N say,
A fundamental improvement on the trivial estimate
is the Pólya–Vinogradov inequality (George Pólya
, I. M. Vinogradov, independently in 1918), stating in big O notation
that
Assuming the generalized Riemann hypothesis
, Hugh Montgomery and R. C. Vaughan have shown that there is the further improvement
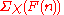
for some function F, generally a polynomial
. A classical result is the case of a quadratic, for example,
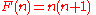
and χ a Legendre symbol
. Here the sum can be evaluated (as −1), a result that is connected to the local zeta-function
of a conic section
.
More generally, such sums for the Jacobi symbol
relate to local zeta-functions of elliptic curve
s and hyperelliptic curves; this means that by means of André Weil
's results, for N = p a prime number
, there are non-trivial bounds
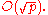
The constant implicit in the notation is linear
in the genus
of the curve in question, and so (Legendre symbol or hyperelliptic case) can be taken as the degree of F. (More general results, for other values of N, can be obtained starting from there.)
Weil's results also led to the Burgess bound, applying to give non-trivial results beyond Pólya–Vinogradov, for R a power of N greater than 1/4.
Assume the modulus N is a prime.
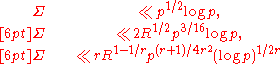
for any integer r ≥ 3.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a character sum is a sum
of values of a Dirichlet character
Dirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
χ modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
N, taken over a given range of values of n. Such sums are basic in a number of questions, for example in the distribution of quadratic residues, and in particular in the classical question of finding an upper bound for the least quadratic nonresidue modulo N. Character sums are often closely linked to exponential sum
Exponential sum
In mathematics, an exponential sum may be a finite Fourier series , or other finite sum formed using the exponential function, usually expressed by means of the functione = \exp.\,...
s by the Gauss sum
Gauss sum
In mathematics, a Gauss sum or Gaussian sum is a particular kind of finite sum of roots of unity, typicallyG := G= \sum \chi\cdot \psi...
s (this is like a finite Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
.)
Assume χ is a nonprincipal Dirichlet character to the modulus N.
Sums over ranges
The sum taken over all residue classes mod N is then zero. This means that the cases of interest will be sums over relatively short ranges, of length R < N say,A fundamental improvement on the trivial estimate
is the Pólya–Vinogradov inequality (George PólyaGeorge Pólya
George Pólya was a Hungarian mathematician. He was a professor of mathematics from 1914 to 1940 at ETH Zürich and from 1940 to 1953 at Stanford University. He made fundamental contributions to combinatorics, number theory, numerical analysis and probability theory...
, I. M. Vinogradov, independently in 1918), stating in big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
that
Assuming the generalized Riemann hypothesis
Generalized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
, Hugh Montgomery and R. C. Vaughan have shown that there is the further improvement
Summing polynomials
Another significant type of character sum is that formed by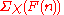for some function F, generally a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
. A classical result is the case of a quadratic, for example,
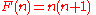
and χ a Legendre symbol
Legendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
. Here the sum can be evaluated (as −1), a result that is connected to the local zeta-function
Local zeta-function
In number theory, a local zeta-functionis a function whose logarithmic derivative is a generating functionfor the number of solutions of a set of equations defined over a finite field F, in extension fields Fk of F.-Formulation:...
of a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
.
More generally, such sums for the Jacobi symbol
Jacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
relate to local zeta-functions of elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s and hyperelliptic curves; this means that by means of André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
's results, for N = p a prime number
Prime
A prime is a natural number that has exactly two distinct natural number divisors: 1 and itself.Prime or PRIME may also refer to:In mathematics:*Prime , the ′ mark, typically used as a suffix...
, there are non-trivial bounds
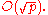
The constant implicit in the notation is linear
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
in the genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
of the curve in question, and so (Legendre symbol or hyperelliptic case) can be taken as the degree of F. (More general results, for other values of N, can be obtained starting from there.)
Weil's results also led to the Burgess bound, applying to give non-trivial results beyond Pólya–Vinogradov, for R a power of N greater than 1/4.
Assume the modulus N is a prime.
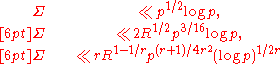
for any integer r ≥ 3.