
Hecke character
Encyclopedia
In number theory
, a Hecke character is a generalisation of a Dirichlet character
, introduced by Erich Hecke
to construct a class of
L-function
s larger than Dirichlet L-functions, and a natural setting for the Dedekind zeta-functions and certain others which have functional equations
analogous to that of the Riemann zeta-function.
A name sometimes used for Hecke character is the German term Größencharakter (often written Grössencharakter, Grossencharakter, Grössencharacter, Grossencharacter etc.).
This definition depends on the definition of a character, which varies slightly between authors: It may be defined as a homomorphism to the non-zero complex numbers (also called a "quasicharacter"), or as a homomorphism to the unit circle in C ("unitary"). Any quasicharacter (of the idele class group) can be written uniquely as a unitary character times a real power of the norm, so there is no big difference between the two definitions.
The conductor of a Hecke character χ is the largest ideal m such that χ is a Hecke character mod m. Here we say that χ is a Hecke character mod m if χ is trivial on ideles whose infinite part is 1 and whose finite part is integral and congruent to 1 mod m.
a character on fractional ideal
s. For a number field K, let
m = mfm∞ be a
K-modulus
, with mf, the "finite part", being an integral ideal of K and m∞, the "infinite part", being a (formal) product of real places of K. Let Im
denote the group of fractional ideals of K relatively prime to mf and
let Pm denote the subgroup of principal fractional ideals (a)
where a is near 1 at each place of m in accordance with the multiplicities of
its factors: for each finite place v in mf, ordv(a - 1) is at least as large as the exponent for v in mf, and a is positive under each real embedding in m∞. A Hecke character with modulus m
is a group homomorphism from Im into the nonzero complex numbers
such that on ideals (a) in Pm its value is equal to the
value at a of a continuous homomorphism to the nonzero complex numbers from the product of the multiplicative groups of all archimedean completions of K where each local component of the homomorphism has the same real part (in the exponent). (Here we embed a into the product of archimedean completions of K using embeddings corresponding to the various archimedean places on K.) Thus a Hecke character may be defined on the ray class group modulo m, which is the quotient Im/Pm.
Strictly speaking, Hecke made the stipulation about behavior on principal ideals for those admitting a totally positive generator. So, in terms of the definition given above, he really only worked with moduli where all real places appeared.
The role of the infinite part m∞ is now subsumed under the notion of
an infinity-type.
This definition is much more complicated than the idelic one, and Hecke's motivation for his definition was to construct L-functions (sometimes referred to as Hecke L-functions) that extend the notion of a Dirichlet L-function from the rationals to other number fields. For a Hecke character , its L-function is defined to be the Dirichlet series
, its L-function is defined to be the Dirichlet series
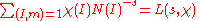
carried out over integral ideals relatively prime to the modulus m of the Hecke character.
The notation N(I) means the norm of an ideal
. The common real part condition governing the behavior of Hecke characters on the subgroups Pm implies these
Dirichlet series are absolutely convergent in some right half-plane. Hecke proved these L-functions have a meromorphic continuation to the whole complex plane, being analytic except for a simple pole of order 1 at s = 1 when the character is trivial. For primitive Hecke characters (defined relative to a modulus in a similar manner to primitive Dirichlet characters), Hecke showed these L-functions satisfy a functional equation relating the values of the L-function of a character and the L-function of its complex conjugate character.
The characters are 'big' (thus explaining the original German term chosen by Hecke) in the sense that the infinity-type when present non-trivially means these characters are not of finite order. The finite-order Hecke characters are all, in a sense, accounted for by class field theory
: their L-functions are Artin L-function
s, as Artin reciprocity
shows. But even a field as simple as the Gaussian field
has Hecke characters that go beyond finite order in a serious way (see the example below). Later developments in complex multiplication
theory indicated that the proper place of the 'big' characters was to provide the Hasse-Weil L-functions for an important class of algebraic varieties (or even motive
s).
's celebrated doctoral dissertation, written under the supervision of Emil Artin
, applied Pontryagin duality
systematically, to remove the need for any special functions. A similar theory was independently developed by Kenkichi Iwasawa
which was the subject of his 1950 ICM talk. A later reformulation in a Bourbaki seminar by Weil (Fonctions zetas et distributions, Séminaire Bourbaki 312, 1966) showed that parts of Tate's proof could be expressed by distribution theory
: the space of distributions (for Schwartz–Bruhat test functions) on the adele group of K transforming under the action of the ideles by a given χ has dimension 1.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a Hecke character is a generalisation of a Dirichlet character
Dirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
, introduced by Erich Hecke
Erich Hecke
Erich Hecke was a German mathematician. He obtained his doctorate in Göttingen under the supervision of David Hilbert. Kurt Reidemeister and Heinrich Behnke were among his students....
to construct a class of
L-function
L-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
s larger than Dirichlet L-functions, and a natural setting for the Dedekind zeta-functions and certain others which have functional equations
Functional equation (L-function)
In mathematics, the L-functions of number theory are expected to have several characteristic properties, one of which is that they satisfy certain functional equations. There is an elaborate theory of what these equations should be, much of which is still conjectural...
analogous to that of the Riemann zeta-function.
A name sometimes used for Hecke character is the German term Größencharakter (often written Grössencharakter, Grossencharakter, Grössencharacter, Grossencharacter etc.).
Definition using ideles
A Hecke character is a character of the idele class group of a number field or global function field.This definition depends on the definition of a character, which varies slightly between authors: It may be defined as a homomorphism to the non-zero complex numbers (also called a "quasicharacter"), or as a homomorphism to the unit circle in C ("unitary"). Any quasicharacter (of the idele class group) can be written uniquely as a unitary character times a real power of the norm, so there is no big difference between the two definitions.
The conductor of a Hecke character χ is the largest ideal m such that χ is a Hecke character mod m. Here we say that χ is a Hecke character mod m if χ is trivial on ideles whose infinite part is 1 and whose finite part is integral and congruent to 1 mod m.
Definition using ideals
The original definition of a Hecke character, going back to Hecke, was in terms ofa character on fractional ideal
Fractional ideal
In mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed...
s. For a number field K, let
m = mfm∞ be a
K-modulus
Modulus (algebraic number theory)
In mathematics, in the field of algebraic number theory, a modulus is a formal product of places of a global field...
, with mf, the "finite part", being an integral ideal of K and m∞, the "infinite part", being a (formal) product of real places of K. Let Im
denote the group of fractional ideals of K relatively prime to mf and
let Pm denote the subgroup of principal fractional ideals (a)
where a is near 1 at each place of m in accordance with the multiplicities of
its factors: for each finite place v in mf, ordv(a - 1) is at least as large as the exponent for v in mf, and a is positive under each real embedding in m∞. A Hecke character with modulus m
is a group homomorphism from Im into the nonzero complex numbers
such that on ideals (a) in Pm its value is equal to the
value at a of a continuous homomorphism to the nonzero complex numbers from the product of the multiplicative groups of all archimedean completions of K where each local component of the homomorphism has the same real part (in the exponent). (Here we embed a into the product of archimedean completions of K using embeddings corresponding to the various archimedean places on K.) Thus a Hecke character may be defined on the ray class group modulo m, which is the quotient Im/Pm.
Strictly speaking, Hecke made the stipulation about behavior on principal ideals for those admitting a totally positive generator. So, in terms of the definition given above, he really only worked with moduli where all real places appeared.
The role of the infinite part m∞ is now subsumed under the notion of
an infinity-type.
This definition is much more complicated than the idelic one, and Hecke's motivation for his definition was to construct L-functions (sometimes referred to as Hecke L-functions) that extend the notion of a Dirichlet L-function from the rationals to other number fields. For a Hecke character
 , its L-function is defined to be the Dirichlet series
, its L-function is defined to be the Dirichlet series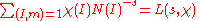
carried out over integral ideals relatively prime to the modulus m of the Hecke character.
The notation N(I) means the norm of an ideal
Norm of an ideal
In commutative algebra, the norm of an ideal is a generalization of a norm of an element in the field extension. It is particularly important in number theory since it measures the size of an ideal of a complicated number ring in terms of an ideal in a less complicated ring...
. The common real part condition governing the behavior of Hecke characters on the subgroups Pm implies these
Dirichlet series are absolutely convergent in some right half-plane. Hecke proved these L-functions have a meromorphic continuation to the whole complex plane, being analytic except for a simple pole of order 1 at s = 1 when the character is trivial. For primitive Hecke characters (defined relative to a modulus in a similar manner to primitive Dirichlet characters), Hecke showed these L-functions satisfy a functional equation relating the values of the L-function of a character and the L-function of its complex conjugate character.
The characters are 'big' (thus explaining the original German term chosen by Hecke) in the sense that the infinity-type when present non-trivially means these characters are not of finite order. The finite-order Hecke characters are all, in a sense, accounted for by class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
: their L-functions are Artin L-function
Artin L-function
In mathematics, an Artin L-function is a type of Dirichlet series associated to a linear representation ρ of a Galois group G. These functions were introduced in the 1923 by Emil Artin, in connection with his research into class field theory. Their fundamental properties, in particular the Artin...
s, as Artin reciprocity
Artin reciprocity
The Artin reciprocity law, established by Emil Artin in a series of papers , is a general theorem in number theory that forms a central part of the global class field theory...
shows. But even a field as simple as the Gaussian field
Gaussian field
Gaussian field may refer to:*A field of Gaussian rationals in number theory*Gaussian free field, a concept in statistical mechanics*A Gaussian random field, a field of Gaussian-distributed random variables...
has Hecke characters that go beyond finite order in a serious way (see the example below). Later developments in complex multiplication
Complex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
theory indicated that the proper place of the 'big' characters was to provide the Hasse-Weil L-functions for an important class of algebraic varieties (or even motive
Motive (algebraic geometry)
In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer...
s).
Special cases
- A Dirichlet character is a Hecke character of finite order.
- A Hilbert character is a Dirichlet character of conductor 1. The number of Hilbert characters is the order of the class group of the field; more precisely, class field theory identifies the Hilbert characters with the characters of the class group.
Examples
- For the field of rational numbers, the idele class group is isomorphic to the product of the positive reals with all the unit groups of the p-adic integers. So a quasicharacter can be written as product of a power of the norm with a Dirichlet character.
- A Hecke character χ of the Gaussian integers of conductor 1 is of the form
- χ((a)) = |a|s(a/|a|)4n
- for s imaginary and n an integer, where a is a generator of the ideal (a). The only units are powers of i, so the factor of 4 in the exponent ensures that the character is well defined on ideals.
Tate's thesis
Hecke's original proof of the functional equation for L(s,χ) used an explicit theta-function. John TateJohn Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
's celebrated doctoral dissertation, written under the supervision of Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
, applied Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
systematically, to remove the need for any special functions. A similar theory was independently developed by Kenkichi Iwasawa
Kenkichi Iwasawa
Kenkichi Iwasawa was a Japanese mathematician who is known for his influence on algebraic number theory.Iwasawa was born in Shinshuku-mura, a town near Kiryū, in Gunma Prefecture...
which was the subject of his 1950 ICM talk. A later reformulation in a Bourbaki seminar by Weil (Fonctions zetas et distributions, Séminaire Bourbaki 312, 1966) showed that parts of Tate's proof could be expressed by distribution theory
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
: the space of distributions (for Schwartz–Bruhat test functions) on the adele group of K transforming under the action of the ideles by a given χ has dimension 1.

