Artin L-function
Encyclopedia
In mathematics
, an Artin L-function is a type of Dirichlet series associated to a linear representation ρ of a Galois group
G. These functions were introduced in the 1923 by Emil Artin
, in connection with his research into class field theory
. Their fundamental properties, in particular the Artin conjecture described below, have turned out to be resistant to easy proof. One of the aims of proposed non-abelian class field theory
is to incorporate the complex-analytic nature of Artin L-functions into a larger framework, such as is provided by automorphic form
s and Langlands' philosophy. So far, only a small part of such a theory has been put on a firm basis.
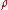, a representation of 
on a finite-dimensional complex vector space 
, where 
is the Galois group of the finite extension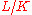 
of number fields, the Artin 
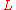-function: 
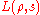is defined by an Euler product
. For each prime ideal
in 
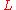, there is an Euler factor, which is easiest to define in the case where 
is unramified in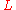 
(true of almost all
). In that case, the Frobenius element 
is defined as a conjugacy class
in
. Therefore the characteristic polynomial
of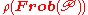
is well-defined. The Euler factor for 
is a slight modification of the characteristic polynomial, equally well-defined,
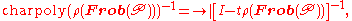
as rational function
in t, evaluated at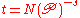
, with 
a complex variable in the usual Riemann zeta function notation. (Here N is the field norm
of an ideal.)
When
is ramified, and I is the inertia group which is a subgroup of G, a similar construction is applied, but to the subspace of V fixed (pointwise) by I.It is arguable more correct to think instead about the coinvariants, the largest quotient space
fixed by I, rather than the invariants, but the result here will be the same. Cf. Hasse-Weil L-function for a similar situation.
The Artin L-function
is then the infinite product over all prime ideals 
of these factors. As Artin reciprocity
shows, when G is an abelian group
these L-functions have a second description (as Dirichlet L-functions when K is the rational number
field, and as Hecke L-functions in general). Novelty comes in with non-abelian
G and their representations.
One application is to give factorisations of Dedekind zeta-function
s, for example in the case of a number field that is Galois over the rational numbers. In accordance with the decomposition of the regular representation
into irreducible representations, such a zeta-function splits into a product of Artin L-functions, for each irreducible representation of G. For example, the simplest case is when G is the symmetric group
on three letters. Since G has an irreducible representation of degree 2, an Artin L-function for such a representation occurs, squared, in the factorisation of the Dedekind zeta-function for such a number field, in a product with the Riemann zeta-function (for the trivial representation
) and an L-function of Dirichlet's type for the signature representation.
. The function L(s, ρ) is related in its values to L(1 − s, ρ*), where ρ* denotes the complex conjugate representation
. More precisely L is replaced by Λ(s, ρ), which is L multiplied by certain gamma factors, and then there is an equation of meromorphic functions
with a certain complex number W(ρ) of absolute value 1. It is the Artin root number. It has been studied deeply with respect to two types of properties. Firstly Langlands and Deligne established a factorisation into Langlands-Deligne local constants; this is significant in relation to conjectural relationships to automorphic representations. Also the case of ρ and ρ* being equivalent representations is exactly the one in which the functional equation has the same L-function on each side. It is, algebraically speaking, the case when ρ is a real representation
or quaternionic representation. The Artin root number is, then, either +1 or −1. The question of which sign occurs is linked to Galois module
theory .
This is known for one-dimensional representations — the L-functions being then associated to Hecke character
s — and in particular for Dirichlet L-functions.
More generally Artin showed that the Artin conjecture is true for all representations induced from 1-dimensional representations. If the Galois group is supersolvable then all representations are of this form so the Artin conjecture holds.
André Weil
proved the Artin conjecture in the case of function fields.
Two dimensional representations are classified by the nature of the image subgroup: it may be cyclic, dihedral, tetrahedral, octahedral, or icosahedral. The Artin conjecture for the cyclic or dihedral case follows easily from Hecke's work. Langlands used the base change lifting
to prove the tetrahedral case, and Tunnell extended his work to cover the octahedral case; Wiles used these cases in his proof of the Taniyama-Shimura conjecture. Richard Taylor
and others have made some progress on the (non-solvable) icosahedral case; this is an active area of research.
Brauer's theorem on induced characters
implies that all Artin L-functions are products of positive and negative integral powers of Hecke L-functions, and are therefore meromorphic in the whole complex plane.
pointed out that the Artin conjecture follows from strong enough results from the Langlands philosophy, relating to the L-functions associated to automorphic representations for GL(n) for all
. More precisely, the Langlands conjectures associate an automorphic representation of the adelic group GLn(AQ) to every n-dimensional irreducible representation of the Galois group, which is a cuspidal representation
if the Galois representation is irreducible, such that the Artin L-function of the Galois representation is the same as the automorphic L-function of the automorphic representation. The Artin conjecture then follows immediately from the known fact that the L-functions of cuspidal automorphic representations are holomorphic. This was one of the major motivations for Langlands' work.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an Artin L-function is a type of Dirichlet series associated to a linear representation ρ of a Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
G. These functions were introduced in the 1923 by Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
, in connection with his research into class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
. Their fundamental properties, in particular the Artin conjecture described below, have turned out to be resistant to easy proof. One of the aims of proposed non-abelian class field theory
Non-abelian class field theory
In mathematics, non-abelian class field theory is a catchphrase, meaning the extension of the results of class field theory, the relatively complete and classical set of results on abelian extensions of any number field K, to the general Galois extension L/K...
is to incorporate the complex-analytic nature of Artin L-functions into a larger framework, such as is provided by automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s and Langlands' philosophy. So far, only a small part of such a theory has been put on a firm basis.
Definition
Given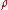, a representation of on a finite-dimensional complex vector space , where is the Galois group of the finite extension 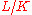of number fields, the Artin 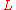-function: 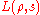is defined by an Euler productEuler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
. For each prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
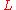in , there is an Euler factor, which is easiest to define in the case where is unramified in 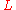(true of almost allAlmost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
). In that case, the Frobenius element is defined as a conjugacy classConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
in
. Therefore the characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of
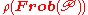is well-defined. The Euler factor for is a slight modification of the characteristic polynomial, equally well-defined,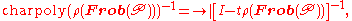as rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
in t, evaluated at
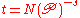, with a complex variable in the usual Riemann zeta function notation. (Here N is the field normField norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
of an ideal.)
When
is ramified, and I is the inertia group which is a subgroup of G, a similar construction is applied, but to the subspace of V fixed (pointwise) by I.It is arguable more correct to think instead about the coinvariants, the largest quotient spaceQuotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
fixed by I, rather than the invariants, but the result here will be the same. Cf. Hasse-Weil L-function for a similar situation.
The Artin L-function
is then the infinite product over all prime ideals of these factors. As Artin reciprocityArtin reciprocity
The Artin reciprocity law, established by Emil Artin in a series of papers , is a general theorem in number theory that forms a central part of the global class field theory...
shows, when G is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
these L-functions have a second description (as Dirichlet L-functions when K is the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
field, and as Hecke L-functions in general). Novelty comes in with non-abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
G and their representations.
One application is to give factorisations of Dedekind zeta-function
Dedekind zeta function
In mathematics, the Dedekind zeta function of an algebraic number field K, generally denoted ζK, is a generalization of the Riemann zeta function—which is obtained by specializing to the case where K is the rational numbers Q...
s, for example in the case of a number field that is Galois over the rational numbers. In accordance with the decomposition of the regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
into irreducible representations, such a zeta-function splits into a product of Artin L-functions, for each irreducible representation of G. For example, the simplest case is when G is the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on three letters. Since G has an irreducible representation of degree 2, an Artin L-function for such a representation occurs, squared, in the factorisation of the Dedekind zeta-function for such a number field, in a product with the Riemann zeta-function (for the trivial representation
Trivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
) and an L-function of Dirichlet's type for the signature representation.
Functional equation
Artin L-functions satisfy a functional equationFunctional equation (L-function)
In mathematics, the L-functions of number theory are expected to have several characteristic properties, one of which is that they satisfy certain functional equations. There is an elaborate theory of what these equations should be, much of which is still conjectural...
. The function L(s, ρ) is related in its values to L(1 − s, ρ*), where ρ* denotes the complex conjugate representation
Complex conjugate representation
In mathematics, if G is a group and ρ is a representation of it over the complex vector space V, then the complex conjugate representation ρ* is defined over the conjugate vector space V* as follows:...
. More precisely L is replaced by Λ(s, ρ), which is L multiplied by certain gamma factors, and then there is an equation of meromorphic functions
- Λ(s, ρ) = W(ρ)Λ(1 − s, ρ*)
with a certain complex number W(ρ) of absolute value 1. It is the Artin root number. It has been studied deeply with respect to two types of properties. Firstly Langlands and Deligne established a factorisation into Langlands-Deligne local constants; this is significant in relation to conjectural relationships to automorphic representations. Also the case of ρ and ρ* being equivalent representations is exactly the one in which the functional equation has the same L-function on each side. It is, algebraically speaking, the case when ρ is a real representation
Real representation
In the mathematical field of representation theory a real representation is usually a representation on a real vector space U, but it can also mean a representation on a complex vector space V with an invariant real structure, i.e., an antilinear equivariant mapj\colon V\to V\,which...
or quaternionic representation. The Artin root number is, then, either +1 or −1. The question of which sign occurs is linked to Galois module
Galois module
In mathematics, a Galois module is a G-module where G is the Galois group of some extension of fields. The term Galois representation is frequently used when the G-module is a vector space over a field or a free module over a ring, but can also be used as a synonym for G-module...
theory .
The Artin conjecture
The Artin conjecture on Artin L-functions states that the Artin L-function L(ρ,s) of a non-trivial irreducible representation ρ is analytic in the whole complex plane.This is known for one-dimensional representations — the L-functions being then associated to Hecke character
Hecke character
In number theory, a Hecke character is a generalisation of a Dirichlet character, introduced by Erich Hecke to construct a class ofL-functions larger than Dirichlet L-functions, and a natural setting for the Dedekind zeta-functions and certain others which have functional equations analogous to...
s — and in particular for Dirichlet L-functions.
More generally Artin showed that the Artin conjecture is true for all representations induced from 1-dimensional representations. If the Galois group is supersolvable then all representations are of this form so the Artin conjecture holds.
André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
proved the Artin conjecture in the case of function fields.
Two dimensional representations are classified by the nature of the image subgroup: it may be cyclic, dihedral, tetrahedral, octahedral, or icosahedral. The Artin conjecture for the cyclic or dihedral case follows easily from Hecke's work. Langlands used the base change lifting
Base change lifting
In mathematics, base change lifting is a method of constructing new automorphic forms from old ones, that corresponds in Langlands philosophy to the operation of restricting a representation of a Galois group to a subgroup....
to prove the tetrahedral case, and Tunnell extended his work to cover the octahedral case; Wiles used these cases in his proof of the Taniyama-Shimura conjecture. Richard Taylor
Richard Taylor (mathematician)
-External links:**...
and others have made some progress on the (non-solvable) icosahedral case; this is an active area of research.
Brauer's theorem on induced characters
Brauer's theorem on induced characters
Brauer's theorem on induced characters, often known as Brauer's induction theorem, and named after Richard Brauer, is a basic result in the branch of mathematics known as character theory, which is, in turn, part of the representation theory of a finite group...
implies that all Artin L-functions are products of positive and negative integral powers of Hecke L-functions, and are therefore meromorphic in the whole complex plane.
pointed out that the Artin conjecture follows from strong enough results from the Langlands philosophy, relating to the L-functions associated to automorphic representations for GL(n) for all
. More precisely, the Langlands conjectures associate an automorphic representation of the adelic group GLn(AQ) to every n-dimensional irreducible representation of the Galois group, which is a cuspidal representationCuspidal representation
In number theory, cuspidal representations are certain representations of algebraic groups that occur discretely in L^2 spaces. The term cuspidal is derived, at a certain distance, from the cusp forms of classical modular form theory...
if the Galois representation is irreducible, such that the Artin L-function of the Galois representation is the same as the automorphic L-function of the automorphic representation. The Artin conjecture then follows immediately from the known fact that the L-functions of cuspidal automorphic representations are holomorphic. This was one of the major motivations for Langlands' work.