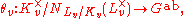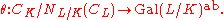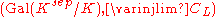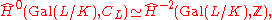Artin reciprocity
Encyclopedia
The Artin reciprocity law, established by Emil Artin
in a series of papers (1924; 1927; 1930), is a general theorem in number theory
that forms a central part of the global class field theory
. The term "reciprocity law" refers to a long line of more concrete number theoretic statements which it generalized, from the quadratic reciprocity law and the reciprocity laws of Eisenstein and Kummer
to Hilbert's
product formula for the norm symbol
. Artin's result provided a partial solution to Hilbert's ninth problem
.
of the absolute Galois group
of a global field
K which is based on the local–global principle and the use of the Frobenius elements. Together with the Takagi existence theorem
, it is used to describe the abelian extension
s of K in terms of arithmetic of K and to understand the behavior of the nonarchimedean places in them. Therefore, the Artin reciprocity law can be interpreted as one of the main theorems of the global class field theory
. It can be used to prove that Artin L-function
s are meromorphic and for the proof of the Chebotarev density theorem.
) extension
L/K of global field
s (such as a finite abelian extension of Q) has a concrete description in terms of prime ideal
s and Frobenius elements.
If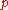
is a prime of K then the decomposition groups of primes 
above 
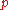are equal in Gal(L/K) since the latter group is abelian
. If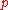
is unramified in L, then the decomposition group 
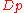is canonically isomorphic to the Galois group of the extension of residue fields 
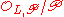over 
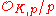. There is therefore a canonically defined Frobenius element in Gal(L/K) denoted by 
or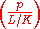 
. If Δ denotes the relative discriminant of L/K, the Artin symbol (or Artin map, or (global) reciprocity map) of L/K is defined on the group of prime-to-Δ fractional ideals, 
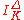, by linearity: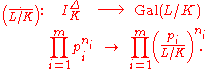
The Artin reciprocity law (or global reciprocity law) states that there is a modulus
c of K such that the Artin map induces an isomorphism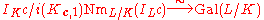
where Kc,1 is the ray modulo c, NmL/K is the norm map associated to L/K and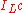
is the fractional ideals of L prime to c. Such a modulus c is called a defining modulus for L/K. The smallest defining modulus is called the conductor of L/K
and typically denoted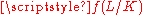
.
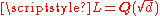, then the Galois group Gal(L/Q) can be identified with {±1}. The discriminant of L over Q is d or 4d depending on whether d ≡ 1 (mod 4) or not. The Artin map is then defined on primes p that do not divide Δ by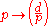
where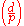
is the Legendre symbol
.
of local field
s with Galois group G. The local reciprocity law describes a canonical isomorphism
called the local Artin symbol.
Let L⁄K be a Galois extension
of global field
s and CL stand for the idèle class group
of L. The maps θv for different places v of K can be assembled into a single global symbol map by multiplying the local components of an idèle class. One of the statements of the Artin reciprocity law is that this results in the canonical isomorphism
A cohomological proof of the global reciprocity law can be achieved by first establishing that
constitutes a class formation
in the sense of Artin and Tate. Then one proves that
where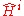
denote the Tate cohomology group
s. Working out the cohomology groups establishes that θ is an isomorphism.
, connects Artin L-function
s associated to abelian extensions of a number field with Hecke L-functions associated to characters of the idèle class group.
A Hecke character
(or Größencharakter) of a number field K is defined to be a quasicharacter of the idèle class group of K. Robert Langlands
interpreted Hecke characters as automorphic form
s on the reductive algebraic group GL(1) over the ring of adeles
of K.
Let E⁄K be an abelian Galois extension with Galois group
G. Then for any character
σ: G → C× (i.e. one-dimensional complex representation
of the group G), there exists a Hecke character χ of K such that
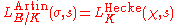
where the left hand side is the Artin L-function associated to the extension with character σ and the right hand side is the Hecke L-function associated with χ, Section 7.D of.
The formulation of the Artin reciprocity law as an equality of L-functions allows formulation of a generalisation to n-dimensional representation, though a direct correspondence still lacking.
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
in a series of papers (1924; 1927; 1930), is a general theorem in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
that forms a central part of the global class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
. The term "reciprocity law" refers to a long line of more concrete number theoretic statements which it generalized, from the quadratic reciprocity law and the reciprocity laws of Eisenstein and Kummer
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
to Hilbert's
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
product formula for the norm symbol
Hilbert symbol
In mathematics, given a local field K, such as the fields of reals or p-adic numbers, whose multiplicative group of non-zero elements is K×, the Hilbert symbol is an algebraic construction, extracted from reciprocity laws, and important in the formulation of local class field theory...
. Artin's result provided a partial solution to Hilbert's ninth problem
Hilbert's ninth problem
Hilbert's ninth problem, from the list of 23 Hilbert's problems , asked to find the most general reciprocity law for the norm residues of k-th order in a general algebraic number field, where k is a power of a prime.- Progress made :...
.
Significance
Artin's reciprocity law implies a description of the abelianizationCommutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
of the absolute Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of a global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
K which is based on the local–global principle and the use of the Frobenius elements. Together with the Takagi existence theorem
Takagi existence theorem
In class field theory, the Takagi existence theorem states that for any number field K there is a one-to-one inclusion reversing correspondence between the finite abelian extensions of K and the generalized ideal class groups defined via a modulus of K.It is called an existence theorem because a...
, it is used to describe the abelian extension
Abelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
s of K in terms of arithmetic of K and to understand the behavior of the nonarchimedean places in them. Therefore, the Artin reciprocity law can be interpreted as one of the main theorems of the global class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
. It can be used to prove that Artin L-function
Artin L-function
In mathematics, an Artin L-function is a type of Dirichlet series associated to a linear representation ρ of a Galois group G. These functions were introduced in the 1923 by Emil Artin, in connection with his research into class field theory. Their fundamental properties, in particular the Artin...
s are meromorphic and for the proof of the Chebotarev density theorem.
Finite extensions of global fields
The definition of the Artin map for a finite (abelianAbelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
) extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
L/K of global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s (such as a finite abelian extension of Q) has a concrete description in terms of prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s and Frobenius elements.
If
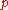is a prime of K then the decomposition groups of primes above 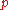are equal in Gal(L/K) since the latter group is abelianAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. If
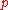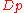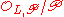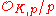is unramified in L, then the decomposition group is canonically isomorphic to the Galois group of the extension of residue fields over . There is therefore a canonically defined Frobenius element in Gal(L/K) denoted by or 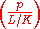. If Δ denotes the relative discriminant of L/K, the Artin symbol (or Artin map, or (global) reciprocity map) of L/K is defined on the group of prime-to-Δ fractional ideals, 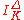, by linearity: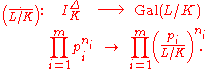The Artin reciprocity law (or global reciprocity law) states that there is a modulus
Modulus (algebraic number theory)
In mathematics, in the field of algebraic number theory, a modulus is a formal product of places of a global field...
c of K such that the Artin map induces an isomorphism
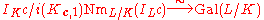
where Kc,1 is the ray modulo c, NmL/K is the norm map associated to L/K and
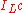is the fractional ideals of L prime to c. Such a modulus c is called a defining modulus for L/K. The smallest defining modulus is called the conductor of L/KConductor (class field theory)
In algebraic number theory, the conductor of a finite abelian extension of local or global fields provides a quantitative measure of the ramification in the extension. The definition of the conductor is related to the Artin map.-Local conductor:...
and typically denoted
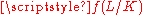.Example: quadratic fields
If d is a squarefree integer, K = Q, and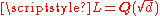, then the Galois group Gal(L/Q) can be identified with {±1}. The discriminant of L over Q is d or 4d depending on whether d ≡ 1 (mod 4) or not. The Artin map is then defined on primes p that do not divide Δ by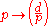where
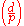is the Legendre symbolLegendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
.
Cohomological interpretation
Let Lv⁄Kv be a Galois extensionGalois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
of local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
s with Galois group G. The local reciprocity law describes a canonical isomorphism
called the local Artin symbol.
Let L⁄K be a Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
of global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s and CL stand for the idèle class group
Adelic algebraic group
In abstract algebra, an adelic algebraic group is a topological group defined by an algebraic group G over a number field K, and the adele ring A = A of K. It consists of the points of G having values in A; the definition of the appropriate topology is straightforward only in case G is a linear...
of L. The maps θv for different places v of K can be assembled into a single global symbol map by multiplying the local components of an idèle class. One of the statements of the Artin reciprocity law is that this results in the canonical isomorphism
A cohomological proof of the global reciprocity law can be achieved by first establishing that
constitutes a class formation
Class formation
In mathematics, a class formation is a structure used to organize the various Galois groups and modules that appear in class field theory. They were invented by Emil Artin and John Tate.-Definitions:...
in the sense of Artin and Tate. Then one proves that
where
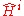denote the Tate cohomology groupTate cohomology group
In mathematics, Tate cohomology groups are a slightly modified form of the usual cohomology groups of a finite group that combine homology and cohomology groups into one sequence...
s. Working out the cohomology groups establishes that θ is an isomorphism.
Alternative statement
An alternative version of the reciprocity law, leading to the Langlands programLanglands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
, connects Artin L-function
Artin L-function
In mathematics, an Artin L-function is a type of Dirichlet series associated to a linear representation ρ of a Galois group G. These functions were introduced in the 1923 by Emil Artin, in connection with his research into class field theory. Their fundamental properties, in particular the Artin...
s associated to abelian extensions of a number field with Hecke L-functions associated to characters of the idèle class group.
A Hecke character
Hecke character
In number theory, a Hecke character is a generalisation of a Dirichlet character, introduced by Erich Hecke to construct a class ofL-functions larger than Dirichlet L-functions, and a natural setting for the Dedekind zeta-functions and certain others which have functional equations analogous to...
(or Größencharakter) of a number field K is defined to be a quasicharacter of the idèle class group of K. Robert Langlands
Robert Langlands
Robert Phelan Langlands is a mathematician, best known as the founder of the Langlands program. He is an emeritus professor at the Institute for Advanced Study...
interpreted Hecke characters as automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s on the reductive algebraic group GL(1) over the ring of adeles
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
of K.
Let E⁄K be an abelian Galois extension with Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
G. Then for any character
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
σ: G → C× (i.e. one-dimensional complex representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the group G), there exists a Hecke character χ of K such that
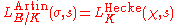
where the left hand side is the Artin L-function associated to the extension with character σ and the right hand side is the Hecke L-function associated with χ, Section 7.D of.
The formulation of the Artin reciprocity law as an equality of L-functions allows formulation of a generalisation to n-dimensional representation, though a direct correspondence still lacking.