Robert Langlands
Encyclopedia
Robert Phelan Langlands (born October 6, 1936, in New Westminster, British Columbia
, Canada
) is a mathematician
, best known as the founder of the Langlands program
. He is an emeritus
professor
at the Institute for Advanced Study
. His work in automorphic form
s and representation theory
has had a major effect on number theory
.
in 1957, and continued on there to receive an M. Sc. in 1958. He then went to Yale University
where he received a Ph.D. in 1960. His academic positions since then include the years 1960-67 at Princeton University, ending up as Associate Professor, and the years 1967-72 at Yale University. He was appointed Hermann Weyl Professor at the Institute for Advanced Study
in 1972, becoming Professor Emeritus in January 2007.
His Ph.D. thesis was on the analytical theory of semi-groups, but he soon moved into representation theory, adapting the methods of Harish-Chandra
to the theory of automorphic forms. His first accomplishment in this field was a formula for the dimension of certain spaces of automorphic form, in which particular types of Harish-Chandra's discrete series appeared.
He next constructed an analytical theory of Eisenstein series
for reductive groups of rank greater than one, thus extending work of Maass, Roelcke and Selberg
from the early 1950s for rank one groups such as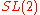
. This amounted to describing in general terms the continuous spectra of arithmetic quotients, and showing that all automorphic forms arise in terms of cusp forms and the residues of Eisenstein series induced from cusp forms on smaller subgroups. As a first application, he proved André Weil
's conjecture about Tamagawa number for the large class of arbitrary simply connected Chevalley groups defined over the rational numbers. Previously this had been known only in a few isolated cases and for certain classical groups where it could be shown by induction.
As a second application of this work, he was able to show meromorphic continuation for a large class of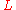
-functions
arising in the theory of automorphic forms, not previously known to have them. These occurred in the constant terms of Eisenstein series, and meromorphicity as well as a weak functional equation were a consequence of functional equations for Eisenstein series. This work led in turn, in the winter of 1966/67, to the now well known conjectures making up what is often called the Langlands program
. Very roughly speaking, they propose a huge generalization of previously known examples of reciprocity, including (a) classical class field theory
, in which characters of local and arithmetic abelian Galois group
s are identified with characters of local multiplicative groups and the idele quotient group, respectively; (b) earlier results of Eichler and Shimura in which the Hasse-Weil zeta functions of arithmetic quotients of the upper half plane are identified with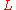
-functions occurring in Hecke's theory of holomorphic automorphic forms. These conjectures were first posed in relatively complete form in a famous letter to Weil, written in January 1967. It was in this letter that he introduced what has since become known as the 
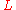-group and along with it, the notion of functoriality.
Functoriality, the
-group, the rigorous introduction of adele groups, and the consequent application of the representation theory of reductive groups over local fields changed drastically the way research in automorphic forms was carried out. Langlands' introduction of (or in cases where others had done previous work, emphasis on) these notions broke up large and to some extent intractable problems into smaller and more manageable pieces. For example, they made the infinite-dimensional representation theory of reductive groups into a major field of mathematical activity.
Functoriality is the conjecture that automorphic forms on different groups should be related in terms of their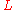
-groups. As one example of this conjecture the letter to Weil raised the possibility of solving the well known conjecture of Emil Artin
regarding the behaviour of Artin's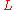
-functions, a hope partly realized in Langlands' later work on base change. In its application to Artin's conjecture, functoriality associated to every 
-dimensional representation of a Galois group
an automorphic representation of the adelic group of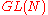
. In the theory of Shimura varieties it associates automorphic representations of other groups to certain 
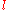-adic Galois representations as well.
The book by Hervé Jacquet
and Langlands on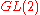
presented a theory of automorphic forms for the general linear group
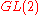, establishing among other things the Jacquet–Langlands correspondence
showing that functoriality was capable of explaining very precisely how automorphic forms for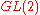
related to those for quaternion algebras. This book applied the adelic trace formula
for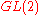
and quaternion algebras to do this. Subsequently James Arthur
, a student of Langlands while he was at Yale, successfully developed the trace formula for groups of higher rank. This has become a major tool in attacking functoriality in general, and in particular has been applied to demonstrating that the Hasse-Weil zeta function
s of certain Shimura varieties
are among the
-functions arising from automorphic forms.
The functoriality conjecture is far from proved, but a special case (the octahedral Artin conjecture
, proved by Langlands and Tunnell) was the starting point of Andrew Wiles
' attack on the Taniyama-Shimura conjecture and Fermat's last theorem
.
In the mid-1980s Langlands turned his attention to physics
, particularly the problems of percolation and conformal invariance.
In recent years he has turned his attention back to automorphic forms, working in particular on a theme he calls `beyond endoscopy'.
In 1995 Langlands started a collaboration with Bill Casselman at the University of British Columbia with the aim of posting nearly all of his writings - including publications, preprints, as well as selected correspondence - on the Internet. The correspondence includes a copy of the original letter to Weil that introduced the
-group.
Langlands has received the 1996 Wolf Prize (which he shared with Andrew Wiles
), the 2005 AMS Steele Prize, the 1980 Jeffery-Williams Prize, the 1988 NAS Award in Mathematics
from the National Academy of Sciences
, the 2006 Nemmers Prize in Mathematics
, and the 2007 Shaw Prize
in Mathematical Sciences (with Richard Taylor
) for his work on automorphic forms.
He was elected a Fellow of the Royal Society of London in 1981.
British Columbia
British Columbia is the westernmost of Canada's provinces and is known for its natural beauty, as reflected in its Latin motto, Splendor sine occasu . Its name was chosen by Queen Victoria in 1858...
, Canada
Canada
Canada is a North American country consisting of ten provinces and three territories. Located in the northern part of the continent, it extends from the Atlantic Ocean in the east to the Pacific Ocean in the west, and northward into the Arctic Ocean...
) is a mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, best known as the founder of the Langlands program
Langlands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
. He is an emeritus
Emeritus
Emeritus is a post-positive adjective that is used to designate a retired professor, bishop, or other professional or as a title. The female equivalent emerita is also sometimes used.-History:...
professor
Professor
A professor is a scholarly teacher; the precise meaning of the term varies by country. Literally, professor derives from Latin as a "person who professes" being usually an expert in arts or sciences; a teacher of high rank...
at the Institute for Advanced Study
Institute for Advanced Study
The Institute for Advanced Study, located in Princeton, New Jersey, United States, is an independent postgraduate center for theoretical research and intellectual inquiry. It was founded in 1930 by Abraham Flexner...
. His work in automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s and representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
has had a major effect on number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
Career
Langlands received an undergraduate degree from the University of British ColumbiaUniversity of British Columbia
The University of British Columbia is a public research university. UBC’s two main campuses are situated in Vancouver and in Kelowna in the Okanagan Valley...
in 1957, and continued on there to receive an M. Sc. in 1958. He then went to Yale University
Yale University
Yale University is a private, Ivy League university located in New Haven, Connecticut, United States. Founded in 1701 in the Colony of Connecticut, the university is the third-oldest institution of higher education in the United States...
where he received a Ph.D. in 1960. His academic positions since then include the years 1960-67 at Princeton University, ending up as Associate Professor, and the years 1967-72 at Yale University. He was appointed Hermann Weyl Professor at the Institute for Advanced Study
Institute for Advanced Study
The Institute for Advanced Study, located in Princeton, New Jersey, United States, is an independent postgraduate center for theoretical research and intellectual inquiry. It was founded in 1930 by Abraham Flexner...
in 1972, becoming Professor Emeritus in January 2007.
His Ph.D. thesis was on the analytical theory of semi-groups, but he soon moved into representation theory, adapting the methods of Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
to the theory of automorphic forms. His first accomplishment in this field was a formula for the dimension of certain spaces of automorphic form, in which particular types of Harish-Chandra's discrete series appeared.
He next constructed an analytical theory of Eisenstein series
Eisenstein series
Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...
for reductive groups of rank greater than one, thus extending work of Maass, Roelcke and Selberg
Atle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
from the early 1950s for rank one groups such as
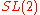. This amounted to describing in general terms the continuous spectra of arithmetic quotients, and showing that all automorphic forms arise in terms of cusp forms and the residues of Eisenstein series induced from cusp forms on smaller subgroups. As a first application, he proved André WeilAndré Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
's conjecture about Tamagawa number for the large class of arbitrary simply connected Chevalley groups defined over the rational numbers. Previously this had been known only in a few isolated cases and for certain classical groups where it could be shown by induction.
As a second application of this work, he was able to show meromorphic continuation for a large class of
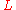-functionsL-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
arising in the theory of automorphic forms, not previously known to have them. These occurred in the constant terms of Eisenstein series, and meromorphicity as well as a weak functional equation were a consequence of functional equations for Eisenstein series. This work led in turn, in the winter of 1966/67, to the now well known conjectures making up what is often called the Langlands program
Langlands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
. Very roughly speaking, they propose a huge generalization of previously known examples of reciprocity, including (a) classical class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
, in which characters of local and arithmetic abelian Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
s are identified with characters of local multiplicative groups and the idele quotient group, respectively; (b) earlier results of Eichler and Shimura in which the Hasse-Weil zeta functions of arithmetic quotients of the upper half plane are identified with
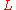-functions occurring in Hecke's theory of holomorphic automorphic forms. These conjectures were first posed in relatively complete form in a famous letter to Weil, written in January 1967. It was in this letter that he introduced what has since become known as the 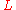-group and along with it, the notion of functoriality.Functoriality, the
-group, the rigorous introduction of adele groups, and the consequent application of the representation theory of reductive groups over local fields changed drastically the way research in automorphic forms was carried out. Langlands' introduction of (or in cases where others had done previous work, emphasis on) these notions broke up large and to some extent intractable problems into smaller and more manageable pieces. For example, they made the infinite-dimensional representation theory of reductive groups into a major field of mathematical activity.Functoriality is the conjecture that automorphic forms on different groups should be related in terms of their
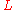-groups. As one example of this conjecture the letter to Weil raised the possibility of solving the well known conjecture of Emil ArtinEmil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
regarding the behaviour of Artin's
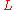-functions, a hope partly realized in Langlands' later work on base change. In its application to Artin's conjecture, functoriality associated to every -dimensional representation of a Galois groupGalois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
an automorphic representation of the adelic group of
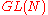. In the theory of Shimura varieties it associates automorphic representations of other groups to certain 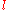-adic Galois representations as well.The book by Hervé Jacquet
Hervé Jacquet
Hervé Jacquet is a French American mathematician born in France in 1939, working in automorphic forms. He is considered one of the founders of the theory of automorphic representations and their associated L-functions, and his results play a central role in modern number theory.-Career:Jacquet...
and Langlands on
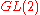presented a theory of automorphic forms for the general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
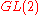, establishing among other things the Jacquet–Langlands correspondenceJacquet–Langlands correspondence
In mathematics, the Jacquet–Langlands correspondence is a correspondence between automorphic forms on GL2 and its twisted forms, proved by using the Selberg trace formula. It was one of the first examples of the Langlands philosophy that maps between L-groups should induce maps between...
showing that functoriality was capable of explaining very precisely how automorphic forms for
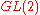related to those for quaternion algebras. This book applied the adelic trace formulaSelberg trace formula
In mathematics, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation of G on the space L2 of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group...
for
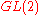and quaternion algebras to do this. Subsequently James ArthurJames Arthur (mathematician)
James Greig Arthur , is a Canadian mathematician and former President of the American Mathematical Society. He is currently in the Mathematics Departmentof the University of Toronto....
, a student of Langlands while he was at Yale, successfully developed the trace formula for groups of higher rank. This has become a major tool in attacking functoriality in general, and in particular has been applied to demonstrating that the Hasse-Weil zeta function
Hasse-Weil zeta function
In mathematics, the Hasse–Weil zeta function attached to an algebraic variety V defined over an algebraic number field K is one of the two most important types of L-function. Such L-functions are called 'global', in that they are defined as Euler products in terms of local zeta functions...
s of certain Shimura varieties
Shimura variety
In number theory, a Shimura variety is a higher-dimensional analogue of a modular curve that arises as a quotient of a Hermitian symmetric space by a congruence subgroup of a reductive algebraic group defined over Q. The term "Shimura variety" applies to the higher-dimensional case, in the case of...
are among the
-functions arising from automorphic forms.The functoriality conjecture is far from proved, but a special case (the octahedral Artin conjecture
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
, proved by Langlands and Tunnell) was the starting point of Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
' attack on the Taniyama-Shimura conjecture and Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
.
In the mid-1980s Langlands turned his attention to physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, particularly the problems of percolation and conformal invariance.
In recent years he has turned his attention back to automorphic forms, working in particular on a theme he calls `beyond endoscopy'.
In 1995 Langlands started a collaboration with Bill Casselman at the University of British Columbia with the aim of posting nearly all of his writings - including publications, preprints, as well as selected correspondence - on the Internet. The correspondence includes a copy of the original letter to Weil that introduced the
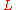-group.Langlands has received the 1996 Wolf Prize (which he shared with Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
), the 2005 AMS Steele Prize, the 1980 Jeffery-Williams Prize, the 1988 NAS Award in Mathematics
NAS Award in Mathematics
The NAS Award in Mathematics is awarded by the U.S. National Academy of Sciences "for excellence of research in the mathematical sciences published within the past ten years." It has been awarded every four years since 1988....
from the National Academy of Sciences
United States National Academy of Sciences
The National Academy of Sciences is a corporation in the United States whose members serve pro bono as "advisers to the nation on science, engineering, and medicine." As a national academy, new members of the organization are elected annually by current members, based on their distinguished and...
, the 2006 Nemmers Prize in Mathematics
Nemmers Prize in Mathematics
The Frederic Esser Nemmers Prize in Mathematics is awarded biennially from Northwestern University. It was initially endowed along with a companion prize, the Erwin Plein Nemmers Prize in Economics, as part of a $14 million donation from the Nemmers brothers. They envisioned creating an award that...
, and the 2007 Shaw Prize
Shaw Prize
The Shaw Prize is an annual award first presented by the Shaw Prize Foundation in 2004. Established in 2002 in Hong Kong, it honours living "individuals, regardless of race, nationality and religious belief, who have achieved significant breakthrough in academic and scientific research or...
in Mathematical Sciences (with Richard Taylor
Richard Taylor (mathematician)
-External links:**...
) for his work on automorphic forms.
He was elected a Fellow of the Royal Society of London in 1981.
See also
- Langlands classificationLanglands classificationIn mathematics, the Langlands classification is a classification of irreducible representations of a reductive Lie group G, suggested by Robert Langlands...
- Langlands decompositionLanglands decompositionIn mathematics, the Langlands decomposition writes a parabolic subgroup P of a semisimple Lie group as a product P=MAN of a reductive subgroup M, an abelian subgroup A, and a nilpotent subgroup N.- Applications :...
- Langlands–Deligne local constantLanglands–Deligne local constantIn mathematics, the Langlands–Deligne local constant is an elementary function associated with a representation of the Weil group of a local field...
- Langlands dual
- Langlands groupLanglands groupIn representation theory, a branch of mathematics, the Langlands dual LG of a reductive algebraic group G is a group that controls the representation theory of G. If G is a group over a field k, LG is an extension of the absolute Galois group of k by a complex Lie group...
- Langlands programLanglands programThe Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....