Hasse-Weil zeta function
Encyclopedia
In mathematics
, the Hasse–Weil zeta function attached to an algebraic variety
V defined over an algebraic number field
K is one of the two most important types of L-function
. Such L-functions are called 'global', in that they are defined as Euler product
s in terms of local zeta functions
. They form one of the two major classes of global L-functions, the other being the L-functions associated to automorphic representations. Conjecturally there is just one essential type of global L-function, with two descriptions (coming from an algebraic variety, coming from an automorphic representation); this would be a vast generalisation of the Taniyama-Shimura conjecture, itself a very deep and recent result in number theory
.
The description of the Hasse–Weil zeta function up to finitely many factors of its Euler product is relatively simple. This follows the initial suggestions of Helmut Hasse
and André Weil
, motivated by the case in which V is a single point, and the Riemann zeta function results.
Taking the case of K the rational number
field Q, and V a non-singular projective variety, we can for almost all
prime number
s p consider the reduction of V modulo p, an algebraic variety Vp over the finite field
Fp with p elements, just by reducing equations for V. Again for almost all p it will be non-singular. We define
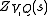
to be the Dirichlet series of the complex variable s, which is the infinite product of the local zeta functions
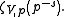
Then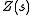
, according to our definition, is well-defined
only up to multiplication by rational function
s in a finite number of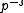
.
Since the indeterminacy is relatively harmless, and has meromorphic continuation everywhere, there is a sense in which the properties of Z(s) do not essentially depend on it. In particular, while the exact form of the functional equation
for Z(s), reflecting in a vertical line in the complex plane, will definitely depend on the 'missing' factors, the existence of some such functional equation does not.
A more refined definition became possible with the development of étale cohomology
; this neatly explains what to do about the missing, 'bad reduction' factors. According to general principles visible in ramification theory
, 'bad' primes carry good information (theory of the conductor). This manifests itself in the étale theory in the Ogg–Néron–Shafarevich criterion for good reduction; namely that there is good reduction, in a definite sense, at all primes p for which the Galois representation ρ on the étale cohomology groups of V is unramified. For those, the definition of local zeta function can be recovered in terms of the characteristic polynomial
of
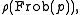
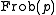being a Frobenius element for p. What happens at the ramified p is that ρ is non-trivial on the inertia group 
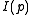for p. At those primes the definition must be 'corrected', taking the largest quotient of the representation ρ on which the inertia group acts by the trivial representation
. With this refinement, the definition of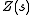
can be upgraded successfully from 'almost all' p to all p participating in the Euler product. The consequences for the functional equation were worked out by Serre
and Deligne in the later 1960s; the functional equation itself has not been proved in general.
N. Then, E has good reduction at all primes p not dividing N, it has multiplicative reduction
at the primes p that exactly divide N (i.e. such that p divides N, but p2 does not; this is written p || N), and it has additive reduction elsewhere (i.e. at the primes where p2 divides N). The Hasse–Weil zeta function of E then takes the form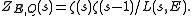
Here, ζ(s) is the usual Riemann zeta function and L(s,E) is called the L-function of E/Q, which takes the form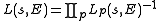
where, for a given prime p,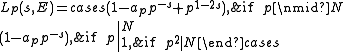
where, in the case of good reduction ap is p + 1 - (number of points of E mod p), and in the case of multiplicative reduction ap is ±1 depending on whether E has split or non-split multiplicative reduction at p.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hasse–Weil zeta function attached to an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
V defined over an algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
K is one of the two most important types of L-function
L-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
. Such L-functions are called 'global', in that they are defined as Euler product
Euler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
s in terms of local zeta functions
Local zeta-function
In number theory, a local zeta-functionis a function whose logarithmic derivative is a generating functionfor the number of solutions of a set of equations defined over a finite field F, in extension fields Fk of F.-Formulation:...
. They form one of the two major classes of global L-functions, the other being the L-functions associated to automorphic representations. Conjecturally there is just one essential type of global L-function, with two descriptions (coming from an algebraic variety, coming from an automorphic representation); this would be a vast generalisation of the Taniyama-Shimura conjecture, itself a very deep and recent result in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
The description of the Hasse–Weil zeta function up to finitely many factors of its Euler product is relatively simple. This follows the initial suggestions of Helmut Hasse
Helmut Hasse
Helmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
and André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
, motivated by the case in which V is a single point, and the Riemann zeta function results.
Taking the case of K the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
field Q, and V a non-singular projective variety, we can for almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s p consider the reduction of V modulo p, an algebraic variety Vp over the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
Fp with p elements, just by reducing equations for V. Again for almost all p it will be non-singular. We define
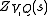
to be the Dirichlet series of the complex variable s, which is the infinite product of the local zeta functions
Local zeta-function
In number theory, a local zeta-functionis a function whose logarithmic derivative is a generating functionfor the number of solutions of a set of equations defined over a finite field F, in extension fields Fk of F.-Formulation:...
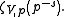
Then
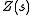, according to our definition, is well-definedWell-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
only up to multiplication by rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s in a finite number of
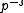.Since the indeterminacy is relatively harmless, and has meromorphic continuation everywhere, there is a sense in which the properties of Z(s) do not essentially depend on it. In particular, while the exact form of the functional equation
Functional equation (L-function)
In mathematics, the L-functions of number theory are expected to have several characteristic properties, one of which is that they satisfy certain functional equations. There is an elaborate theory of what these equations should be, much of which is still conjectural...
for Z(s), reflecting in a vertical line in the complex plane, will definitely depend on the 'missing' factors, the existence of some such functional equation does not.
A more refined definition became possible with the development of étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
; this neatly explains what to do about the missing, 'bad reduction' factors. According to general principles visible in ramification theory
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
, 'bad' primes carry good information (theory of the conductor). This manifests itself in the étale theory in the Ogg–Néron–Shafarevich criterion for good reduction; namely that there is good reduction, in a definite sense, at all primes p for which the Galois representation ρ on the étale cohomology groups of V is unramified. For those, the definition of local zeta function can be recovered in terms of the characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of
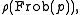
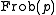being a Frobenius element for p. What happens at the ramified p is that ρ is non-trivial on the inertia group 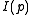for p. At those primes the definition must be 'corrected', taking the largest quotient of the representation ρ on which the inertia group acts by the trivial representationTrivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
. With this refinement, the definition of
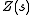can be upgraded successfully from 'almost all' p to all p participating in the Euler product. The consequences for the functional equation were worked out by SerreJean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
and Deligne in the later 1960s; the functional equation itself has not been proved in general.
Example: Elliptic curve over Q
Let E be an elliptic curve over Q of conductorConductor of an abelian variety
In mathematics, in Diophantine geometry, the conductor of an abelian variety defined over a local or global field F is a measure of how "bad" the bad reduction at some prime is...
N. Then, E has good reduction at all primes p not dividing N, it has multiplicative reduction
Semistable elliptic curve
In algebraic geometry, a semistable abelian variety is an abelian variety defined over a global or local field, which is characterized by how it reduces at the primes of the field....
at the primes p that exactly divide N (i.e. such that p divides N, but p2 does not; this is written p || N), and it has additive reduction elsewhere (i.e. at the primes where p2 divides N). The Hasse–Weil zeta function of E then takes the form
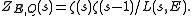
Here, ζ(s) is the usual Riemann zeta function and L(s,E) is called the L-function of E/Q, which takes the form
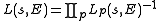
where, for a given prime p,
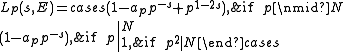
where, in the case of good reduction ap is p + 1 - (number of points of E mod p), and in the case of multiplicative reduction ap is ±1 depending on whether E has split or non-split multiplicative reduction at p.