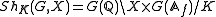Shimura variety
Encyclopedia
In number theory
, a Shimura variety is a higher-dimensional analogue of a modular curve
that arises as a quotient of a Hermitian symmetric space
by a congruence subgroup of a reductive algebraic group defined over Q. The term "Shimura variety" applies to the higher-dimensional case, in the case of one-dimensional varieties one speaks of Shimura curves. Hilbert modular surface
s and Siegel modular varieties
are among the best known classes of Shimura varieties.
Special instances of Shimura varieties were originally introduced by Goro Shimura
in the course of his generalization of the complex multiplication
theory. Shimura showed that while initially defined analytically, they are arithmetic objects, in the sense that they admit models defined
over a number field, the reflex field of the Shimura variety. In the 1970s, Pierre Deligne
created an axiomatic framework for the work of Shimura. Around the same time Robert Langlands
remarked that Shimura varieties form a natural realm of examples for which equivalence between motivic and automorphic L-functions postulated in the Langlands program
can be tested. Automorphic form
s realized in the cohomology
of a Shimura variety are more amenable to study than general automorphic forms; in particular, there is a construction attaching Galois representations to them.
of the multiplicative group from complex numbers to real numbers. It is a real algebraic group
, whose group of R-points, S(R), is C* and group of C-points is C*×C*. A Shimura datum is a pair (G, X) consisting of a reductive algebraic group G defined over the field Q of rational numbers and a G(R)-conjugacy class
X of homomorphisms
h: S → GR satisfying the following axioms:
It follows from these axioms that X has a unique structure of a complex manifold
(possibly, disconnected) such that for every representation ρ: GR → GL(V), the family (V, ρ ⋅ h) is a holomorphic family of Hodge structure
s; moreover, it forms a variation of Hodge structure, and X is a finite disjoint union of hermitian symmetric domains.
of Q. For any sufficiently small compact open subgroup K of G(Aƒ), the double coset
space
is a finite disjoint union of locally symmetric varieties of the form Γ \ X+, where the plus superscript indicates a connected component. The varieties ShK(G,X) are complex algebraic varieties and they form an inverse system
over all sufficiently small compact open subgroups K. This inverse system
admits a natural right action of G(Aƒ). It is called the Shimura variety associated with the Shimura datum (G, X) and denoted Sh(G, X).
s Γ, algebraic varieties of the form Γ \ X = ShK(G,X) and their compactifications
were introduced in a series of papers of Goro Shimura
during the 1960s. Shimura's approach, later presented in his monograph, was largely phenomenological, pursuing the widest generalizations of the reciprocity law formulation of complex multiplication
theory. In retrospect, the name "Shimura variety" was introduced by Deligne
, who proceeded to isolate the abstract features that played role in Shimura's theory. In Deligne's formulation, Shimura varieties are parameter spaces of certain types of Hodge structure
s. Thus they form a natural higher-dimensional generalization of modular curve
s viewed as moduli space
s of elliptic curve
s with level structure. In many cases, the moduli problems to which Shimura varieties are solutions have been likewise identified.
division algebra
over F. The multiplicative group D× gives rise to a canonical Shimura variety. Its dimension d is the number of infinite places over which D splits. In particular, if d = 1 (for example, if F = Q and D ⊗ R ≅ M2(R)), fixing a sufficiently small arithmetic subgroup of D×, one gets a Shimura curve, and curves arising from this construction are already compact (i.e. projective).
Some examples of Shimura curves with explicitly known equations are given by the Hurwitz curves of low genus:
and by the Fermat curve
of degree 7.
and, therefore, arithmetical significance. It forms the starting point in his formulation of the reciprocity law, where an important role is played by certain arithmetically defined special points.
The qualitative nature of the Zariski closure of sets of special points on a Shimura variety is described by the André-Oort conjecture. Conditional results have been obtained on this conjecture, assuming a Generalized Riemann Hypothesis
.
. The prototypical theorem, the Eichler–Shimura congruence relation
, implies that the Hasse-Weil zeta function
of a modular curve is a product of L-functions associated to explicitly determined modular form
s of weight 2. Indeed, it was in the process of generalization of this theorem that Goro Shimura introduced his varieties and proved his reciprocity law. Zeta functions of Shimura varieties associated with the group GL2 over other number fields and its inner forms (i.e. multiplicative groups of quaternion algebras) were studied by Eichler, Shimura, Kuga, Sato, and Ihara. On the basis of their results, Robert Langlands
made a prediction that the Hasse-Weil zeta function of any algebraic variety
W defined over a number field would be a product of positive and negative powers of automorphic L-functions, i.e. it should arise from a collection of automorphic representations. However philosophically natural it may be to expect such a description, statements of this type have only been proved when W is a Shimura variety. In the words of Langlands:
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a Shimura variety is a higher-dimensional analogue of a modular curve
Modular curve
In number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...
that arises as a quotient of a Hermitian symmetric space
Hermitian symmetric space
In mathematics, a Hermitian symmetric space is a Kähler manifold M which, as a Riemannian manifold, is a Riemannian symmetric space. Equivalently, M is a Riemannian symmetric space with a parallel complex structure with respect to which the Riemannian metric is Hermitian...
by a congruence subgroup of a reductive algebraic group defined over Q. The term "Shimura variety" applies to the higher-dimensional case, in the case of one-dimensional varieties one speaks of Shimura curves. Hilbert modular surface
Hilbert modular surface
In mathematics, a Hilbert modular surface is one of the surfaces obtained by taking a quotient of a product of two copies of the upper half-plane by a Hilbert modular group....
s and Siegel modular varieties
Siegel modular form
In mathematics, Siegel modular forms are a major type of automorphic form. These stand in relation to the conventional elliptic modular forms as abelian varieties do in relation to elliptic curves; the complex manifolds constructed as in the theory are basic models for what a moduli space for...
are among the best known classes of Shimura varieties.
Special instances of Shimura varieties were originally introduced by Goro Shimura
Goro Shimura
is a Japanese mathematician, and currently a professor emeritus of mathematics at Princeton University.Shimura was a colleague and a friend of Yutaka Taniyama...
in the course of his generalization of the complex multiplication
Complex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
theory. Shimura showed that while initially defined analytically, they are arithmetic objects, in the sense that they admit models defined
Field of definition
In mathematics, the field of definition of an algebraic variety V is essentially the smallest field to which the coefficients of the polynomials defining V can belong...
over a number field, the reflex field of the Shimura variety. In the 1970s, Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
created an axiomatic framework for the work of Shimura. Around the same time Robert Langlands
Robert Langlands
Robert Phelan Langlands is a mathematician, best known as the founder of the Langlands program. He is an emeritus professor at the Institute for Advanced Study...
remarked that Shimura varieties form a natural realm of examples for which equivalence between motivic and automorphic L-functions postulated in the Langlands program
Langlands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
can be tested. Automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s realized in the cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of a Shimura variety are more amenable to study than general automorphic forms; in particular, there is a construction attaching Galois representations to them.
Shimura datum
Let S = ResC/R Gm be the Weil restrictionWeil restriction
In mathematics, restriction of scalars is a functor which, for any finite extension of fields L/k and any algebraic variety X over L, produces another variety ResL/kX, defined over k...
of the multiplicative group from complex numbers to real numbers. It is a real algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
, whose group of R-points, S(R), is C* and group of C-points is C*×C*. A Shimura datum is a pair (G, X) consisting of a reductive algebraic group G defined over the field Q of rational numbers and a G(R)-conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
X of homomorphisms
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
h: S → GR satisfying the following axioms:
- For any h in X, only weights (0,0), (1,−1), (−1,1) may occur in gC, i.e. the complexified Lie algebra of G decomposes into a direct sum
- where for any z ∈ S, h(z) acts trivially on the first summand and via
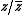(respectively, 
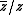) on the second (respectively, third) summand.
- The adjoint action of h(i) induces a Cartan involution on the adjoint group of GR.
- The adjoint group of GR does not admit a factor H defined over Q such that the projection of h on H is trivial.
It follows from these axioms that X has a unique structure of a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
(possibly, disconnected) such that for every representation ρ: GR → GL(V), the family (V, ρ ⋅ h) is a holomorphic family of Hodge structure
Hodge structure
In mathematics, a Hodge structure, named after W. V. D. Hodge, is an algebraic structure at the level of linear algebra, similar to the one that Hodge theory gives to the cohomology groups of a smooth and compact Kähler manifold...
s; moreover, it forms a variation of Hodge structure, and X is a finite disjoint union of hermitian symmetric domains.
Shimura variety
Let Aƒ be the ring of adelesAdele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
of Q. For any sufficiently small compact open subgroup K of G(Aƒ), the double coset
Double coset
In mathematics, an double coset in G, where G is a group and H and K are subgroups of G, is an equivalence class for the equivalence relation defined on G by...
space
is a finite disjoint union of locally symmetric varieties of the form Γ \ X+, where the plus superscript indicates a connected component. The varieties ShK(G,X) are complex algebraic varieties and they form an inverse system
Inverse system
In mathematics, an inverse system in a category C is a functor from a small cofiltered category I to C. An inverse system is sometimes called a pro-object in C. The dual concept is a direct system.-The category of inverse systems:...
over all sufficiently small compact open subgroups K. This inverse system
admits a natural right action of G(Aƒ). It is called the Shimura variety associated with the Shimura datum (G, X) and denoted Sh(G, X).
History
For special types of hermitian symmetric domains and congruence subgroupCongruence subgroup
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2x2 integer matrices of determinant 1, such that the off-diagonal entries are even.An importance class of congruence...
s Γ, algebraic varieties of the form Γ \ X = ShK(G,X) and their compactifications
Baily–Borel compactification
In mathematics, the Baily–Borel compactification is a compactification of a quotient of a Hermitian symmetric space by an arithmetic group, introduced by .-Example:...
were introduced in a series of papers of Goro Shimura
Goro Shimura
is a Japanese mathematician, and currently a professor emeritus of mathematics at Princeton University.Shimura was a colleague and a friend of Yutaka Taniyama...
during the 1960s. Shimura's approach, later presented in his monograph, was largely phenomenological, pursuing the widest generalizations of the reciprocity law formulation of complex multiplication
Complex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
theory. In retrospect, the name "Shimura variety" was introduced by Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
, who proceeded to isolate the abstract features that played role in Shimura's theory. In Deligne's formulation, Shimura varieties are parameter spaces of certain types of Hodge structure
Hodge structure
In mathematics, a Hodge structure, named after W. V. D. Hodge, is an algebraic structure at the level of linear algebra, similar to the one that Hodge theory gives to the cohomology groups of a smooth and compact Kähler manifold...
s. Thus they form a natural higher-dimensional generalization of modular curve
Modular curve
In number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...
s viewed as moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
s of elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s with level structure. In many cases, the moduli problems to which Shimura varieties are solutions have been likewise identified.
Examples
Let F be a totally real number field and D a quaternionQuaternion algebra
In mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars , i.e...
division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
over F. The multiplicative group D× gives rise to a canonical Shimura variety. Its dimension d is the number of infinite places over which D splits. In particular, if d = 1 (for example, if F = Q and D ⊗ R ≅ M2(R)), fixing a sufficiently small arithmetic subgroup of D×, one gets a Shimura curve, and curves arising from this construction are already compact (i.e. projective).
Some examples of Shimura curves with explicitly known equations are given by the Hurwitz curves of low genus:
- Klein quarticKlein quarticIn hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
(genus 3) - Macbeath surfaceMacbeath surfaceIn Riemann surface theory and hyperbolic geometry, the Macbeath surface, also called Macbeath's curve or the Fricke–Macbeath curve, is the genus-7 Hurwitz surface....
(genus 7) - First Hurwitz tripletFirst Hurwitz tripletIn the mathematical theory of Riemann surfaces, the first Hurwitz triplet is a triple of distinct Hurwitz surfaces with the identical automorphism group of the lowest possible genus, namely 14 . The explanation for this phenomenon is arithmetic...
(genus 14)
and by the Fermat curve
Fermat curve
In mathematics, the Fermat curve is the algebraic curve in the complex projective plane defined in homogeneous coordinates by the Fermat equationX^n + Y^n = Z^n.\ Therefore in terms of the affine plane its equation is...
of degree 7.
Canonical models and special points
Each Shimura variety can be defined over a canonical number field E called the reflex field. This important result due to Shimura shows that Shimura varieties, which a priori are only complex manifolds, have an algebraic field of definitionField of definition
In mathematics, the field of definition of an algebraic variety V is essentially the smallest field to which the coefficients of the polynomials defining V can belong...
and, therefore, arithmetical significance. It forms the starting point in his formulation of the reciprocity law, where an important role is played by certain arithmetically defined special points.
The qualitative nature of the Zariski closure of sets of special points on a Shimura variety is described by the André-Oort conjecture. Conditional results have been obtained on this conjecture, assuming a Generalized Riemann Hypothesis
Generalized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
.
Role in the Langlands program
Shimura varieties play an outstanding role in the Langlands programLanglands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
. The prototypical theorem, the Eichler–Shimura congruence relation
Eichler–Shimura congruence relation
In number theory, the Eichler–Shimura congruence relation expresses the local L-function of a modular curve at a prime p in terms of the eigenvalues of Hecke operators...
, implies that the Hasse-Weil zeta function
Hasse-Weil zeta function
In mathematics, the Hasse–Weil zeta function attached to an algebraic variety V defined over an algebraic number field K is one of the two most important types of L-function. Such L-functions are called 'global', in that they are defined as Euler products in terms of local zeta functions...
of a modular curve is a product of L-functions associated to explicitly determined modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s of weight 2. Indeed, it was in the process of generalization of this theorem that Goro Shimura introduced his varieties and proved his reciprocity law. Zeta functions of Shimura varieties associated with the group GL2 over other number fields and its inner forms (i.e. multiplicative groups of quaternion algebras) were studied by Eichler, Shimura, Kuga, Sato, and Ihara. On the basis of their results, Robert Langlands
Robert Langlands
Robert Phelan Langlands is a mathematician, best known as the founder of the Langlands program. He is an emeritus professor at the Institute for Advanced Study...
made a prediction that the Hasse-Weil zeta function of any algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
W defined over a number field would be a product of positive and negative powers of automorphic L-functions, i.e. it should arise from a collection of automorphic representations. However philosophically natural it may be to expect such a description, statements of this type have only been proved when W is a Shimura variety. In the words of Langlands: