
Complex conjugate representation
Encyclopedia
In mathematics
, if G is a group
and ρ is a representation
of it over the complex
vector space
V, then the complex conjugate representation ρ* is defined over the conjugate vector space V* as follows:
ρ* is also a representation, as you may check explicitly.
If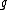 is a real
is a real
Lie algebra
and ρ is a representation of it over the vector space V, then the conjugate representation ρ* is defined over the conjugate vector space V* as follows:
ρ* is also a representation, as you may check explicitly.
If two real Lie algebras have the same complexification
, and we have a complex representation of the complexified Lie algebra, their conjugate representations are still going to be different. See spinor
for some examples associated with spinor representations of the spin groups Spin(p+q) and Spin(p,q).
If is a *-Lie algebra (a complex Lie algebra with a * operation which is compatible with the Lie bracket),
is a *-Lie algebra (a complex Lie algebra with a * operation which is compatible with the Lie bracket),
For a unitary representation
, the dual representation and the conjugate representation coincide.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, if G is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and ρ is a representation
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of it over the complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V, then the complex conjugate representation ρ* is defined over the conjugate vector space V* as follows:
- ρ*(g) is the conjugate of ρ(g) for all g in G.
ρ* is also a representation, as you may check explicitly.
If
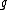 is a real
is a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
and ρ is a representation of it over the vector space V, then the conjugate representation ρ* is defined over the conjugate vector space V* as follows:
- ρ*(u) is the conjugate of ρ(u) for all u in
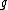 .
.
ρ* is also a representation, as you may check explicitly.
If two real Lie algebras have the same complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
, and we have a complex representation of the complexified Lie algebra, their conjugate representations are still going to be different. See spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
for some examples associated with spinor representations of the spin groups Spin(p+q) and Spin(p,q).
If
 is a *-Lie algebra (a complex Lie algebra with a * operation which is compatible with the Lie bracket),
is a *-Lie algebra (a complex Lie algebra with a * operation which is compatible with the Lie bracket),- ρ*(u) is the conjugate of −ρ(u*) for all u in
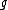
For a unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
, the dual representation and the conjugate representation coincide.

