
Unitary representation
Encyclopedia
In mathematics
, a unitary representation of a group
G is a linear representation π of G on a complex Hilbert space
V such that π(g) is a unitary operator
for every g ∈ G. The general theory is well-developed in case G is a locally compact (Hausdorff) topological group
and the representations are strongly continuous.
The theory has been widely applied in quantum mechanics
since the 1920s, particularly influenced by Hermann Weyl
's 1928 book Gruppentheorie und Quantenmechanik. One of the pioneers in constructing a general theory of unitary representations, for any group G rather than just for particular groups useful in applications, was George Mackey
.
. In the case of an abelian group G, a fairly complete picture of the representation theory of G is given by Pontryagin duality
. In general, the unitary equivalence classes of irreducible unitary representations of G make up its unitary dual. This set can be identified with the spectrum of the C*-algebra associated to G by the group C*-algebra
construction. This is a topological space
.
The general form of the Plancherel theorem
tries to describe the regular representation of G on L2(G) by means of a measure
on the unitary dual. For G abelian this is given by the Pontryagin duality theory. For G compact
, this is done by the Peter-Weyl theorem; in that case the unitary dual is a discrete space
, and the measure attaches an atom to each point of mass equal to its degree.
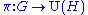
such that g → π(g) ξ is a norm continuous function for every ξ ∈ H.
Note that if G is a Lie group
, the Hilbert space also admits underlying smooth and analytic structures. A vector ξ in H is said to be smooth or analytic if the map g → π(g) ξ is smooth or analytic (in the norm or weak topologies on H). Smooth vectors are dense in H by a classical argument of Lars Gårding
, since convolution by smooth functions of compact support yields smooth vectors. Analytic vectors are dense by a classical argument of Edward Nelson
, amplified by Roe Goodman, since vectors in the image of a heat operator e–tD, corresponding to an elliptic differential operator D in the universal enveloping algebra
of G, are analytic. Not only do smooth or analytic vectors form dense subspaces; they also form common cores for the unbounded skew-adjoint operators corresponding to the elements of the Lie algebra
, in the sense of spectral theory
.
, the orthogonal complement is again a closed invariant subspace. This is at the level of an observation, but is a fundamental property. For example, it implies that finite dimensional unitary representations are always a direct sum of irreducible representations, in the algebraic sense.
Since unitary representations are much easier to handle than the general case, it is natural to consider unitarizable representations, those that become unitary on the introduction of a suitable complex Hilbert space structure. This works very well for finite groups, and more generally for compact group
s, by an averaging argument applied to an arbitrary hermitian structure. For example, a natural proof of Maschke's theorem
is by this route.
Lie group
s. All irreducible unitary representations are admissible
(or rather their Harish-Chandra module
s are), and the admissible representations are given by the Langlands classification
, and it is easy to tell which of them have a non-trivial invariant sesquilinear form. The problem is that it is in general hard to tell when this form is positive definite. For many reductive Lie groups this has been solved; see representation theory of SL2(R)
and representation theory of the Lorentz group for examples.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a unitary representation of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is a linear representation π of G on a complex Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
V such that π(g) is a unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
for every g ∈ G. The general theory is well-developed in case G is a locally compact (Hausdorff) topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
and the representations are strongly continuous.
The theory has been widely applied in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
since the 1920s, particularly influenced by Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
's 1928 book Gruppentheorie und Quantenmechanik. One of the pioneers in constructing a general theory of unitary representations, for any group G rather than just for particular groups useful in applications, was George Mackey
George Mackey
George Whitelaw Mackey was an American mathematician. Mackey earned his bachelor of arts at Rice University in 1938 and obtained his Ph.D. at Harvard University in 1942 under the direction of Marshall H. Stone...
.
Context in harmonic analysis
The theory of unitary representations of groups is closely connected with harmonic analysisHarmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
. In the case of an abelian group G, a fairly complete picture of the representation theory of G is given by Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
. In general, the unitary equivalence classes of irreducible unitary representations of G make up its unitary dual. This set can be identified with the spectrum of the C*-algebra associated to G by the group C*-algebra
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
construction. This is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
.
The general form of the Plancherel theorem
Plancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
tries to describe the regular representation of G on L2(G) by means of a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on the unitary dual. For G abelian this is given by the Pontryagin duality theory. For G compact
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
, this is done by the Peter-Weyl theorem; in that case the unitary dual is a discrete space
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
, and the measure attaches an atom to each point of mass equal to its degree.
Formal definitions
Let G be a topological group. A strongly continuous unitary representation of G on a Hilbert space H is a group homomorphism from G into the unitary group of H,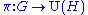
such that g → π(g) ξ is a norm continuous function for every ξ ∈ H.
Note that if G is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, the Hilbert space also admits underlying smooth and analytic structures. A vector ξ in H is said to be smooth or analytic if the map g → π(g) ξ is smooth or analytic (in the norm or weak topologies on H). Smooth vectors are dense in H by a classical argument of Lars Gårding
Lars Gårding
Lars Gårding is a Swedish mathematician. He has made notable contributions to the study of partial differential operators. He is a professor emeritus of mathematics at Lund University in Sweden...
, since convolution by smooth functions of compact support yields smooth vectors. Analytic vectors are dense by a classical argument of Edward Nelson
Edward Nelson
Edward Nelson is a professor in the Mathematics Department at Princeton University. He is known for his work on mathematical physics and mathematical logic...
, amplified by Roe Goodman, since vectors in the image of a heat operator e–tD, corresponding to an elliptic differential operator D in the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of G, are analytic. Not only do smooth or analytic vectors form dense subspaces; they also form common cores for the unbounded skew-adjoint operators corresponding to the elements of the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, in the sense of spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
.
Complete reducibility
A unitary representation is completely reducible, in the sense that for any closed invariant subspaceInvariant subspace
In mathematics, an invariant subspace of a linear mappingfrom some vector space V to itself is a subspace W of V such that T is contained in W...
, the orthogonal complement is again a closed invariant subspace. This is at the level of an observation, but is a fundamental property. For example, it implies that finite dimensional unitary representations are always a direct sum of irreducible representations, in the algebraic sense.
Since unitary representations are much easier to handle than the general case, it is natural to consider unitarizable representations, those that become unitary on the introduction of a suitable complex Hilbert space structure. This works very well for finite groups, and more generally for compact group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
s, by an averaging argument applied to an arbitrary hermitian structure. For example, a natural proof of Maschke's theorem
Maschke's theorem
In mathematics, Maschke's theorem, named after Heinrich Maschke, is a theorem in group representation theory that concerns the decomposition of representations of a finite group into irreducible pieces...
is by this route.
Unitarizability and the unitary dual question
In general, for non-compact groups, it is a more serious question which representations are unitarizable. One of the important unsolved problems in mathematics is the description of the unitary dual, the effective classification of irreducible unitary representations of all real reductiveReductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s. All irreducible unitary representations are admissible
Admissible representation
In mathematics, admissible representations are a well-behaved class of representations used in the representation theory of reductive Lie groups and locally compact totally disconnected groups. They were introduced by Harish-Chandra....
(or rather their Harish-Chandra module
Harish-Chandra module
In mathematics, specifically in the representation theory of Lie groups, a Harish-Chandra module is a representation of a real Lie group, associated to a general representation, with regularity and finiteness conditions...
s are), and the admissible representations are given by the Langlands classification
Langlands classification
In mathematics, the Langlands classification is a classification of irreducible representations of a reductive Lie group G, suggested by Robert Langlands...
, and it is easy to tell which of them have a non-trivial invariant sesquilinear form. The problem is that it is in general hard to tell when this form is positive definite. For many reductive Lie groups this has been solved; see representation theory of SL2(R)
Representation theory of SL2(R)
In mathematics, the main results concerning irreducible unitary representations of the Lie group SL are due to Gelfand and Naimark , V...
and representation theory of the Lorentz group for examples.
See also
- Unitary representation of a star Lie superalgebra
- Representation theory of SL2(R)Representation theory of SL2(R)In mathematics, the main results concerning irreducible unitary representations of the Lie group SL are due to Gelfand and Naimark , V...
- Representations of the Lorentz groupRepresentations of the Lorentz groupThe Lorentz group of theoretical physics has a variety of representations, corresponding to particles with integer and half-integer spins in quantum field theory. These representations are normally constructed out of spinors....
- Zonal spherical functionZonal spherical functionIn mathematics, a zonal spherical function or often just spherical function is a function on a locally compact group G with compact subgroup K that arises as the matrix coefficient of a K-invariant vector in an irreducible representation of G...
- Induced representations
- Stone-von Neumann theorem

