
Preferential attachment
Encyclopedia
A preferential attachment process is any of a class of processes in which some quantity, typically some form of wealth or credit, is distributed among a number of individuals or objects according to how much they already have, so that those who are already wealthy receive more than those who are not. "Preferential attachment" is only the most recent of many names that have been given to such processes. They are also referred to under the names "Yule process", "Gibrat's law
", "cumulative advantage", "the rich get richer", and, less correctly, the "Matthew effect
". The principal reason for scientific interest in preferential attachment is that it can, under suitable circumstances, generate power law
distributions.
Related articles: Capital accumulation
, Wealth condensation, The rich get richer and the poor get poorer
, Matthew effect (sociology)
urn process
, meaning a process in which discrete units of wealth, usually called "balls", are added in a random or partly random fashion to a set of objects or containers, usually called "urns". A preferential attachment process is an urn process in which additional balls are added continuously to the system and are distributed among the urns as an increasing function of the number of balls the urns already have. In the most commonly studied examples, the number of urns also increases continuously, although this is not a necessary condition for preferential attachment and examples have been studied with constant or even decreasing numbers of urns.
A classic example of a preferential attachment process is the growth in the number of species
per genus
in some higher taxon
of biotic organisms. New genera ("urns") are added to a taxon whenever a newly appearing species is considered sufficiently different from its predecessors that it does not belong in any of the current genera. New species ("balls") are added as old ones speciate
(i.e., split in two) and, assuming that new species belong to the same genus as their parent (except for those that start new genera), the probability that a species is added to a new genus will be proportional to the number of species the genus already has. This process, first studied by Yule
, is a linear
preferential attachment process, since the rate at which genera accrue new species is linear in the number they already have.
Linear preferential attachment processes in which the number of urns increases are known to produce a distribution of balls over the urns following the so-called Yule distribution. In the most general form of the process, balls are added to the system at an overall rate of m new balls for each new urn. Each newly created urn starts out with k0 balls and further balls are added to urns at a rate proportional to the number k that they already have plus a constant a > −k0. With these definitions, the fraction P(k) of urns having k balls in the limit of long time is given by
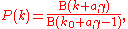
for k ≥ k0 (and zero otherwise), where B(x, y) is the Euler beta function:
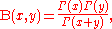
with Γ(x) being the standard gamma function
, and
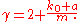
The beta function behaves asymptotically as B(x, y) ~ x−y for large x and fixed y, which implies that for large values of k we have
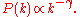
In other words, the preferential attachment process generates a "long-tailed" distribution following a Pareto distribution or power law
in its tail. This is the primary reason for the historical interest in preferential attachment: the species distribution and many other phenomena are observed empirically to follow power laws and the preferential attachment process is a leading candidate mechanism to explain this behavior. Preferential attachment is considered a possible candidate for, among other things, the distribution of the sizes of cities, the wealth of extremely wealthy individuals, the number of citations received by learned publications, and the number of links to pages on the World Wide Web.
The general model described here includes many other specific models as special cases. In the species/genus example above, for instance, each genus starts out with a single species (k0 = 1) and gains new species in direct proportion to the number it already has (a = 0), and hence P(k) = B(k, γ)/B(k0, γ − 1) with γ = 2 + 1/m. Similarly the Price model for scientific citations corresponds to the case k0 = 0, a = 1 and the widely studied Barabási-Albert model corresponds to k0 = m, a = 0.
Preferential attachment is sometimes referred to as the Matthew effect
, but the two are not precisely equivalent. The Matthew effect, first discussed by Robert Merton
, is named for a passage in the biblical
Gospel of Matthew
: "For everyone who has will be given more, and he will have an abundance. Whoever does not have, even what he has will be taken from him." (Matthew
25:29, New International Version
.) The preferential attachment process does not incorporate the taking away part. An urn process that includes both the giving and the taking away would produce a log-normal distribution rather than a power law . This point may be moot, however, since the scientific insight behind the Matthew effect is in any case entirely different. Qualitatively it is intended to describe not a mechanical multiplicative effect like preferential attachment but a specific human behavior in which people are more likely to give credit to the famous than to the little known. The classic example of the Matthew effect is a scientific discovery made simultaneously by two different people, one well known and the other little known. It is claimed that under these circumstances people tend more often to credit the discovery to the well-known scientist. Thus the real-world phenomenon the Matthew effect is intended to describe is quite distinct from (though certainly related to) preferential attachment.
in 1925, who used it to explain the power-law distribution of the number of species per genus of flowering plants. The process is sometimes called a "Yule process" in his honor. Yule was able to show that the process gave rise to a distribution with a power-law tail, but the details of his proof are, by today's standards, contorted and difficult, since the modern tools of stochastic process theory did not yet exist and he was forced to use more cumbersome methods of proof.
Most modern treatments of preferential attachment make use of the master equation
method, whose use in this context was pioneered by Simon
in 1955, in work on the distribution of sizes of cities and other phenomena.
The first application of preferential attachment to learned citations was given by Price
in 1976. (He referred to the process as a "cumulative advantage" process.) His was also the first application of the process to the growth of a network, producing what would now be called a scale-free network
. It is in the context of network growth that the process is most frequently studied today. Price also promoted preferential attachment as a possible explanation for power laws in many other phenomena, including Lotka's law of scientific productivity and Bradford's law
of journal use.
The application of preferential attachment to the growth of the World Wide Web was proposed by Barabási and Albert
in 1999. Barabási and Albert also coined the name "preferential attachment" by which the process is best known today and suggested that the process might apply to the growth of other networks as well.
Gibrat's law
Gibrat's law, sometimes called Gibrat's rule of proportionate growth is a rule defined by Robert Gibrat stating that the size of a firm and its growth rate are independent. The law proportionate growth gives rise to a distribution that is log-normal...
", "cumulative advantage", "the rich get richer", and, less correctly, the "Matthew effect
Matthew effect (sociology)
In sociology, the Matthew effect is the phenomenon where "the rich get richer and the poor get poorer". Those who possess power and economic or social capital can leverage those resources to gain more power or capital. The term was first coined by sociologist Robert K...
". The principal reason for scientific interest in preferential attachment is that it can, under suitable circumstances, generate power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
distributions.
Related articles: Capital accumulation
Capital accumulation
The accumulation of capital refers to the gathering or amassing of objects of value; the increase in wealth through concentration; or the creation of wealth. Capital is money or a financial asset invested for the purpose of making more money...
, Wealth condensation, The rich get richer and the poor get poorer
The rich get richer and the poor get poorer
"The rich get richer and the poor get poorer" is a catchphrase and proverb, frequently used in discussing economic inequality...
, Matthew effect (sociology)
Matthew effect (sociology)
In sociology, the Matthew effect is the phenomenon where "the rich get richer and the poor get poorer". Those who possess power and economic or social capital can leverage those resources to gain more power or capital. The term was first coined by sociologist Robert K...
Definition
A preferential attachment process is a stochasticStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
urn process
Urn problem
In probability and statistics, an urn problem is an idealized mental exercise in which some objects of real interest are represented as colored balls in an urn or other container....
, meaning a process in which discrete units of wealth, usually called "balls", are added in a random or partly random fashion to a set of objects or containers, usually called "urns". A preferential attachment process is an urn process in which additional balls are added continuously to the system and are distributed among the urns as an increasing function of the number of balls the urns already have. In the most commonly studied examples, the number of urns also increases continuously, although this is not a necessary condition for preferential attachment and examples have been studied with constant or even decreasing numbers of urns.
A classic example of a preferential attachment process is the growth in the number of species
Species
In biology, a species is one of the basic units of biological classification and a taxonomic rank. A species is often defined as a group of organisms capable of interbreeding and producing fertile offspring. While in many cases this definition is adequate, more precise or differing measures are...
per genus
Genus
In biology, a genus is a low-level taxonomic rank used in the biological classification of living and fossil organisms, which is an example of definition by genus and differentia...
in some higher taxon
Taxon
|thumb|270px|[[African elephants]] form a widely-accepted taxon, the [[genus]] LoxodontaA taxon is a group of organisms, which a taxonomist adjudges to be a unit. Usually a taxon is given a name and a rank, although neither is a requirement...
of biotic organisms. New genera ("urns") are added to a taxon whenever a newly appearing species is considered sufficiently different from its predecessors that it does not belong in any of the current genera. New species ("balls") are added as old ones speciate
Speciation
Speciation is the evolutionary process by which new biological species arise. The biologist Orator F. Cook seems to have been the first to coin the term 'speciation' for the splitting of lineages or 'cladogenesis,' as opposed to 'anagenesis' or 'phyletic evolution' occurring within lineages...
(i.e., split in two) and, assuming that new species belong to the same genus as their parent (except for those that start new genera), the probability that a species is added to a new genus will be proportional to the number of species the genus already has. This process, first studied by Yule
Udny Yule
George Udny Yule FRS , usually known as Udny Yule, was a British statistician, born at Beech Hill, a house in Morham near Haddington, Scotland and died in Cambridge, England. His father, also George Udny Yule, and a nephew, were knighted. His uncle was the noted orientalist Sir Henry Yule...
, is a linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
preferential attachment process, since the rate at which genera accrue new species is linear in the number they already have.
Linear preferential attachment processes in which the number of urns increases are known to produce a distribution of balls over the urns following the so-called Yule distribution. In the most general form of the process, balls are added to the system at an overall rate of m new balls for each new urn. Each newly created urn starts out with k0 balls and further balls are added to urns at a rate proportional to the number k that they already have plus a constant a > −k0. With these definitions, the fraction P(k) of urns having k balls in the limit of long time is given by
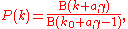
for k ≥ k0 (and zero otherwise), where B(x, y) is the Euler beta function:
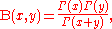
with Γ(x) being the standard gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, and
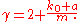
The beta function behaves asymptotically as B(x, y) ~ x−y for large x and fixed y, which implies that for large values of k we have
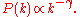
In other words, the preferential attachment process generates a "long-tailed" distribution following a Pareto distribution or power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
in its tail. This is the primary reason for the historical interest in preferential attachment: the species distribution and many other phenomena are observed empirically to follow power laws and the preferential attachment process is a leading candidate mechanism to explain this behavior. Preferential attachment is considered a possible candidate for, among other things, the distribution of the sizes of cities, the wealth of extremely wealthy individuals, the number of citations received by learned publications, and the number of links to pages on the World Wide Web.
The general model described here includes many other specific models as special cases. In the species/genus example above, for instance, each genus starts out with a single species (k0 = 1) and gains new species in direct proportion to the number it already has (a = 0), and hence P(k) = B(k, γ)/B(k0, γ − 1) with γ = 2 + 1/m. Similarly the Price model for scientific citations corresponds to the case k0 = 0, a = 1 and the widely studied Barabási-Albert model corresponds to k0 = m, a = 0.
Preferential attachment is sometimes referred to as the Matthew effect
Matthew effect
The Matthew effect may refer to:* Matthew effect , the phenomenon in sociology where "the rich get richer and the poor get poorer"* Matthew effect , the phenomenon in education that has been observed in research on how new readers acquire the skills to read...
, but the two are not precisely equivalent. The Matthew effect, first discussed by Robert Merton
Robert Merton
Robert Merton may refer to:*Robert K. Merton , American sociologist*Robert C. Merton , American economist, Nobel Laureate, MIT professor, son of Robert K. Merton...
, is named for a passage in the biblical
Bible
The Bible refers to any one of the collections of the primary religious texts of Judaism and Christianity. There is no common version of the Bible, as the individual books , their contents and their order vary among denominations...
Gospel of Matthew
Gospel of Matthew
The Gospel According to Matthew is one of the four canonical gospels, one of the three synoptic gospels, and the first book of the New Testament. It tells of the life, ministry, death, and resurrection of Jesus of Nazareth...
: "For everyone who has will be given more, and he will have an abundance. Whoever does not have, even what he has will be taken from him." (Matthew
Gospel of Matthew
The Gospel According to Matthew is one of the four canonical gospels, one of the three synoptic gospels, and the first book of the New Testament. It tells of the life, ministry, death, and resurrection of Jesus of Nazareth...
25:29, New International Version
New International Version
The New International Version is an English translation of the Christian Bible. Published by Zondervan in the United States and by Hodder & Stoughton in the UK, it has become one of the most popular modern translations in history.-History:...
.) The preferential attachment process does not incorporate the taking away part. An urn process that includes both the giving and the taking away would produce a log-normal distribution rather than a power law . This point may be moot, however, since the scientific insight behind the Matthew effect is in any case entirely different. Qualitatively it is intended to describe not a mechanical multiplicative effect like preferential attachment but a specific human behavior in which people are more likely to give credit to the famous than to the little known. The classic example of the Matthew effect is a scientific discovery made simultaneously by two different people, one well known and the other little known. It is claimed that under these circumstances people tend more often to credit the discovery to the well-known scientist. Thus the real-world phenomenon the Matthew effect is intended to describe is quite distinct from (though certainly related to) preferential attachment.
History
The first rigorous consideration of preferential attachment seems to be that of YuleUdny Yule
George Udny Yule FRS , usually known as Udny Yule, was a British statistician, born at Beech Hill, a house in Morham near Haddington, Scotland and died in Cambridge, England. His father, also George Udny Yule, and a nephew, were knighted. His uncle was the noted orientalist Sir Henry Yule...
in 1925, who used it to explain the power-law distribution of the number of species per genus of flowering plants. The process is sometimes called a "Yule process" in his honor. Yule was able to show that the process gave rise to a distribution with a power-law tail, but the details of his proof are, by today's standards, contorted and difficult, since the modern tools of stochastic process theory did not yet exist and he was forced to use more cumbersome methods of proof.
Most modern treatments of preferential attachment make use of the master equation
Master equation
In physics and chemistry and related fields, master equations are used to describe the time-evolution of a system that can be modelled as being in exactly one of countable number of states at any given time, and where switching between states is treated probabilistically...
method, whose use in this context was pioneered by Simon
Herbert Simon
Herbert Alexander Simon was an American political scientist, economist, sociologist, and psychologist, and professor—most notably at Carnegie Mellon University—whose research ranged across the fields of cognitive psychology, cognitive science, computer science, public administration, economics,...
in 1955, in work on the distribution of sizes of cities and other phenomena.
The first application of preferential attachment to learned citations was given by Price
Derek J. de Solla Price
Derek John de Solla Price was a physicist, historian of science, and information scientist,credited as the father of scientometrics.-Biography:...
in 1976. (He referred to the process as a "cumulative advantage" process.) His was also the first application of the process to the growth of a network, producing what would now be called a scale-free network
Scale-free network
A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P of nodes in the network having k connections to other nodes goes for large values of k as...
. It is in the context of network growth that the process is most frequently studied today. Price also promoted preferential attachment as a possible explanation for power laws in many other phenomena, including Lotka's law of scientific productivity and Bradford's law
Bradford's law
Bradford's law is a pattern first described by Samuel C. Bradford in 1934 that estimates the exponentially diminishing returns of extending a search for references in science journals...
of journal use.
The application of preferential attachment to the growth of the World Wide Web was proposed by Barabási and Albert
BA model
The Barabási–Albert model is an algorithm for generating random scale-free networks using a preferential attachment mechanism. Scale-free networks are widely observed in natural and man-made systems, including the Internet, the world wide web, citation networks, and some social...
in 1999. Barabási and Albert also coined the name "preferential attachment" by which the process is best known today and suggested that the process might apply to the growth of other networks as well.
See also
- Assortative mixingAssortative mixingIn the study of complex networks, assortative mixing, or assortativity, is a bias in favor of connections between network nodes with similar characteristics. In the specific case of social networks, assortative mixing is also known as homophily...
- Stochastic processes
- Power lawPower lawA power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
- Yule–Simon distribution
- Simon modelSimon model-Motivation:Aiming to account for the wide range of empirical distributions following a power-law, Herbert Simon proposed a class of stochastic models that results in a power-law distribution function. It models the dynamics of a system...
- Complex networkComplex networkIn the context of network theory, a complex network is a graph with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in real graphs...
- BA modelBA modelThe Barabási–Albert model is an algorithm for generating random scale-free networks using a preferential attachment mechanism. Scale-free networks are widely observed in natural and man-made systems, including the Internet, the world wide web, citation networks, and some social...
- Wealth condensation
- Chinese restaurant process
- Bose–Einstein condensation: a network theory approach
- Double jeopardy (marketing)Double jeopardy (marketing)Double jeopardy is an empirical law in marketing where, with few exceptions, the lower market share brands in a market have both far fewer buyers in a time period and also lower brand loyalty....

