Chinese restaurant process
Encyclopedia
In probability theory
, the Chinese restaurant process is a discrete-time stochastic process
, whose value at any positive-integer time n is a partition
Bn of the set {1, 2, 3, ..., n} whose probability distribution
is determined as follows. At time n = 1, the trivial partition { {1} } is obtained with probability 1. At time n + 1 the element n + 1 is either:
The random partition so generated is exchangeable in the sense that relabeling {1, ..., n} does not change the distribution of the partition, and it is consistent in the sense that the law of the partition of n − 1 obtained by removing the element n from the random partition at time n is the same as the law of the random partition at time n − 1.
with an infinite number of circular tables, each with infinite capacity. Customer 1 is seated at an unoccupied table with probability 1. At time n + 1, a new customer chooses uniformly at random to sit at one of the following n + 1 places: directly to the left of one of the n customers already sitting at an occupied table, or at a new, unoccupied circular table. Clearly, each table corresponds to a block of a random partition. (For an account of the custom in actual Chinese restaurants, see table sharing
). It is then immediate that the probability assigned to any particular partition (ignoring the order in which customers sit around any particular table) is
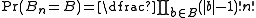
where b is a block in the partition B and |b| is the size (i.e. number of elements) of b. The restaurant analogy is due to Pitman and Dubins, and first appears in print in .
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the Chinese restaurant process is a discrete-time stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
, whose value at any positive-integer time n is a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
Bn of the set {1, 2, 3, ..., n} whose probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
is determined as follows. At time n = 1, the trivial partition { {1} } is obtained with probability 1. At time n + 1 the element n + 1 is either:
- added to one of the blocks of the partition Bn, where each block is chosen with probability |b|/(n + 1) where |b| is the size of the block, or
- added to the partition Bn as a new singleton block, with probability 1/(n + 1).
The random partition so generated is exchangeable in the sense that relabeling {1, ..., n} does not change the distribution of the partition, and it is consistent in the sense that the law of the partition of n − 1 obtained by removing the element n from the random partition at time n is the same as the law of the random partition at time n − 1.
Definition
One fancifully imagines a Chinese restaurantChinese cuisine
Chinese cuisine is any of several styles originating in the regions of China, some of which have become highly popular in other parts of the world – from Asia to the Americas, Australia, Western Europe and Southern Africa...
with an infinite number of circular tables, each with infinite capacity. Customer 1 is seated at an unoccupied table with probability 1. At time n + 1, a new customer chooses uniformly at random to sit at one of the following n + 1 places: directly to the left of one of the n customers already sitting at an occupied table, or at a new, unoccupied circular table. Clearly, each table corresponds to a block of a random partition. (For an account of the custom in actual Chinese restaurants, see table sharing
Table sharing
Table sharing refers to the seating at a single table of multiple separate parties—individual customers or groups of customers who may not know each other.-Overview:...
). It is then immediate that the probability assigned to any particular partition (ignoring the order in which customers sit around any particular table) is
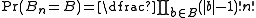
where b is a block in the partition B and |b| is the size (i.e. number of elements) of b. The restaurant analogy is due to Pitman and Dubins, and first appears in print in .
Generalization
This construction can be generalized to a model with two parameters, α and θ, commonly called the discount and strength (or concentration) parameters. At time n + 1, the next customer to arrive finds |B| occupied tables and decides to sit at an empty table with probability-
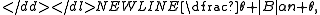
or at an occupied table b of size |b| with probability
-
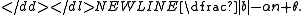
In order for the construction to define a valid probability measureProbability measureIn mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
it is necessary to suppose that either α < 0 and θ = - Lα for some L ∈ {1, 2, ...}; or that 0 ≤ α ≤ 1 and θ > −α.
Under this model the probability assigned to any particular partition B of n is
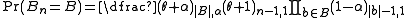
where, by convention,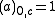
, and for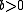 
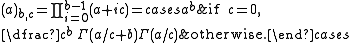
Thus the partition probability can be expressed in terms of the Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
as
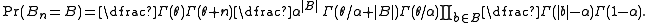
In the one-parameter case, where
is zero, this simplifies to
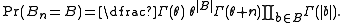
As before, the probability assigned to any particular partition depends only on the block sizes, so as before the random partition is exchangeable in the sense described above. The consistency property still holds, as before, by construction.
If α = 0, the probability distribution of the random partition of the integer n thus generated is the Ewens distribution with parameter θ, used in population geneticsPopulation geneticsPopulation genetics is the study of allele frequency distribution and change under the influence of the four main evolutionary processes: natural selection, genetic drift, mutation and gene flow. It also takes into account the factors of recombination, population subdivision and population...
and the unified neutral theory of biodiversityUnified neutral theory of biodiversityThe unified neutral theory of biodiversity and biogeography is a hypothesis and the title of a monograph by ecologist Stephen Hubbell...
.
Derivation
Here is one way to derive this partition probability. Let Ci be the random block into which the number i is added, for i = 1, 2, 3, ... . Then
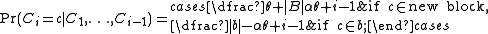
The probability that Bn is any particular partition of the set { 1, ..., n } is the product of these probabilities as i runs from 1 to n. Now consider the size of block b: it increases by 1 each time we add one element into it. When the last element in block b is to be added in, the block size is (|b| − 1). For example, consider this sequence of choices: (generate a new block b)(join b)(join b)(join b). In the end, block b has 4 elements and the product of the numerators in the above equation gets θ · 1 · 2 · 3. Following this logic, we obtain Pr(Bn = B) as above.
Expected number of tables
For the one parameter case, with α = 0 and 0 < θ < ∞, the expected number of tables, given that there are
seated customers, is
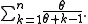
In general case (α > 0) the expected number of occupied tables is
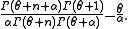
The Indian buffet process
It is possible to adapt the model such that each data point is no longer uniquely associated with a class (i.e. we are no longer constructing a partition), but may be associated with any combination of the classes. This strains the restaurant-tables analogy but can instead be described as a process in which each diner samples from some subset of an infinite selection of dishes on offer at a buffet. The probability that a particular diner samples a particular dish is proportional to the popularity of the dish among diners so far, and in addition the diner may sample from the untested dishes. This has been named the Indian buffet process and can be used to infer latent features in data.
Applications
The Chinese restaurant process is closely connected to Dirichlet processDirichlet processIn probability theory, a Dirichlet process is a stochastic process that can be thought of as a probability distribution whose domain is itself a random distribution...
es and Polya's urn schemePolya urn modelIn statistics, a Polya urn model , named after George Pólya, is a type of statistical model used as an idealized mental exercise to understand the nature of certain statistical distributions.In an urn model, objects of real interest are represented as colored balls in an urn or...
, and therefore useful in applications of nonparametric Bayesian methods including Bayesian statisticsBayesian statisticsBayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
. The Generalized Chinese Restaurant Process is closely related to Pitman–Yor processPitman–Yor processIn probability theory, a Pitman–Yor process, denoted PY, is a stochastic process whose sample path is a probability distribution. A random sample from this process is a finite-dimensional Pitman–Yor distribution, named after Jim Pitman and Marc Yor...
. These processes have been used in many applications, including modeling text, clustering biological microarray data, biodiversity modellingUnified neutral theory of biodiversityThe unified neutral theory of biodiversity and biogeography is a hypothesis and the title of a monograph by ecologist Stephen Hubbell...
and detecting objects in images .
External links
- A talk by Michael I. JordanMichael I. JordanMichael I. Jordan is a leading researcher in machine learning and artificial intelligence. Jordan was a prime mover behind popularising Bayesian networks in the machine learning community and is known for pointing out links between machine learning and statistics...
on the CRP:- http://videolectures.net/icml05_jordan_dpcrp/
- A talk by Michael I. Jordan
-