
Pochhammer contour
Encyclopedia
In mathematics, the Pochhammer contour, introduced by and , is a contour in the complex plane
with two points removed, used for contour integration. If A and B are loops around the two points, both starting at some fixed point P, then the Pochhammer contour is the commutator ABA−1B−1, where the superscript −1 denotes a path taken in the opposite direction. With the two points taken as 0 and 1, the fixed basepoint P being on the real axis between them, an example is the path that starts at P, encircles the point 1 in the counter-clockwise direction and returns to P, then encircles 0 counter-clockwise and returns to P, after that circling 1 and then 0 clockwise, before coming back to P. The class of the contour is an actual commutator
when it is considered in the fundamental group
with basepoint P of the complement in the complex plane (or Riemann sphere
) of the two points looped. When it comes to taking contour integrals, moving basepoint from P to another choice Q makes no difference to the result, since there will be cancellation of integrals from P to Q and back.
to zero. Its winding number
about any point is 0 despite the fact that within the doubly punctured plane it cannot be shrunk to a single point.
integral
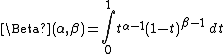
provided that the real parts of α and β are positive, which may be converted into an integral over the Pochhammer contour C as
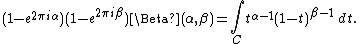
The contour integral converges for all values of α and β and so gives the analytic continuation
of the beta function. A similar method can be applied to Euler's integral for the hypergeometric function to give its analytic continuation.
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
with two points removed, used for contour integration. If A and B are loops around the two points, both starting at some fixed point P, then the Pochhammer contour is the commutator ABA−1B−1, where the superscript −1 denotes a path taken in the opposite direction. With the two points taken as 0 and 1, the fixed basepoint P being on the real axis between them, an example is the path that starts at P, encircles the point 1 in the counter-clockwise direction and returns to P, then encircles 0 counter-clockwise and returns to P, after that circling 1 and then 0 clockwise, before coming back to P. The class of the contour is an actual commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
when it is considered in the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
with basepoint P of the complement in the complex plane (or Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
) of the two points looped. When it comes to taking contour integrals, moving basepoint from P to another choice Q makes no difference to the result, since there will be cancellation of integrals from P to Q and back.
Homologous to zero but not homotopic to zero
Within the doubly punctured plane this curve is homologous to zero but not homotopicHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
to zero. Its winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
about any point is 0 despite the fact that within the doubly punctured plane it cannot be shrunk to a single point.
Applications
The beta function is given by Euler'sLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
integral
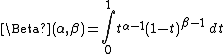
provided that the real parts of α and β are positive, which may be converted into an integral over the Pochhammer contour C as
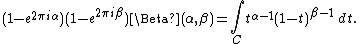
The contour integral converges for all values of α and β and so gives the analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of the beta function. A similar method can be applied to Euler's integral for the hypergeometric function to give its analytic continuation.

