
Stochastic processes and boundary value problems
Encyclopedia
In mathematics
, some boundary value problem
s can be solved using the methods of stochastic analysis. Perhaps the most celebrated example is Shizuo Kakutani
's 1944 solution of the Dirichlet problem
for the Laplace operator
using Brownian motion
. However, it turns out that for a large class of semi-elliptic
second-order partial differential equations the associated Dirichlet boundary value problem can be solved using an Itō process that solves an associated stochastic differential equation
.
and connected set
) in Rn. Let Δ be the Laplace operator
, let g be a bounded function
on the boundary
∂D, and consider the problem
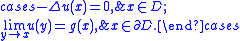
It can be shown that if a solution u exists, then u(x) is the expected value
of g(x) at the (random) first exit point from D for a canonical Brownian motion
starting at x. See theorem 3 in Kakutani 1944, p. 710.
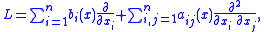
where the coefficients bi and aij are continuous function
s and all the eigenvalues of the matrix
a(x) = (aij(x)) are non-negative. Let f ∈ C(D; R) and g ∈ C(∂D; R). Consider the Poisson problem
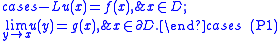
The idea of the stochastic method for solving this problem is as follows. First, one finds an Itō diffusion
X whose infinitesimal generator
A coincides with L on compactly-supported C2 functions f : Rn → R. For example, X can be taken to be the solution to the stochastic differential equation
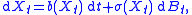
where B is n-dimensional Brownian motion, b has components bi as above, and the matrix field
σ is chosen so that
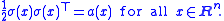
For a point x ∈ Rn, let Px denote the law of X given initial datum X0 = x, and let Ex denote expectation with respect to Px. Let τD denote the first exit time of X from D.
In this notation, the candidate solution for (P1) is
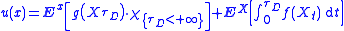
provided that g is a bounded function
and that

It turns out that one further condition is required:
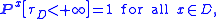
i.e., for all x, the process X starting at x almost surely
leaves D in finite time. Under this assumption, the candidate solution above reduces to
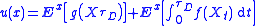
and solves (P1) in the sense that if denotes the characteristic operator for X (which agrees with A on C2 functions), then
denotes the characteristic operator for X (which agrees with A on C2 functions), then
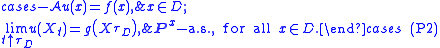
Moreover, if v ∈ C2(D; R) satisfies (P2) and there exists a constant C such that, for all x ∈ D,
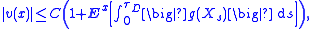
then v = u.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, some boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s can be solved using the methods of stochastic analysis. Perhaps the most celebrated example is Shizuo Kakutani
Shizuo Kakutani
was a Japanese-born American mathematician, best known for his eponymous fixed-point theorem.Kakutani attended Tohoku University in Sendai, where his advisor was Tatsujirō Shimizu. Early in his career he spent two years at the Institute for Advanced Study in Princeton at the invitation of the...
's 1944 solution of the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
for the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
using Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
. However, it turns out that for a large class of semi-elliptic
Semi-elliptic operator
In mathematics — specifically, in the theory of partial differential equations — a semi-elliptic operator is a partial differential operator satisfying a positivity condition slightly weaker than that of being an elliptic operator...
second-order partial differential equations the associated Dirichlet boundary value problem can be solved using an Itō process that solves an associated stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
.
Introduction: Kakutani's solution to the classical Dirichlet problem
Let D be a domain (an openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and connected set
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
) in Rn. Let Δ be the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, let g be a bounded function
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
on the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
∂D, and consider the problem
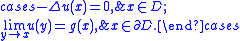
It can be shown that if a solution u exists, then u(x) is the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of g(x) at the (random) first exit point from D for a canonical Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
starting at x. See theorem 3 in Kakutani 1944, p. 710.
The Dirichlet-Poisson problem
Let D be a domain in Rn and let L be a semi-elliptic differential operator on C2(Rn; R) of the form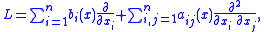
where the coefficients bi and aij are continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s and all the eigenvalues of the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
a(x) = (aij(x)) are non-negative. Let f ∈ C(D; R) and g ∈ C(∂D; R). Consider the Poisson problem
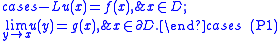
The idea of the stochastic method for solving this problem is as follows. First, one finds an Itō diffusion
Ito diffusion
In mathematics — specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation, used in Physics to describe the brownian motion of a particle subjected to a potential in a...
X whose infinitesimal generator
Infinitesimal generator (stochastic processes)
In mathematics — specifically, in stochastic analysis — the infinitesimal generator of a stochastic process is a partial differential operator that encodes a great deal of information about the process...
A coincides with L on compactly-supported C2 functions f : Rn → R. For example, X can be taken to be the solution to the stochastic differential equation
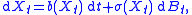
where B is n-dimensional Brownian motion, b has components bi as above, and the matrix field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
σ is chosen so that
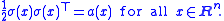
For a point x ∈ Rn, let Px denote the law of X given initial datum X0 = x, and let Ex denote expectation with respect to Px. Let τD denote the first exit time of X from D.
In this notation, the candidate solution for (P1) is
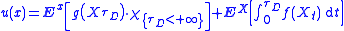
provided that g is a bounded function
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
and that

It turns out that one further condition is required:
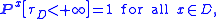
i.e., for all x, the process X starting at x almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
leaves D in finite time. Under this assumption, the candidate solution above reduces to
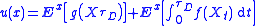
and solves (P1) in the sense that if
 denotes the characteristic operator for X (which agrees with A on C2 functions), then
denotes the characteristic operator for X (which agrees with A on C2 functions), then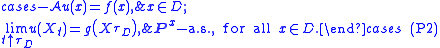
Moreover, if v ∈ C2(D; R) satisfies (P2) and there exists a constant C such that, for all x ∈ D,
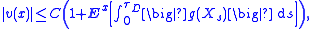
then v = u.

