Several complex variables
Encyclopedia
The theory of function
s of several complex variables is the branch of mathematics
dealing with functions
on the space Cn of n-tuple
s of complex number
s. As in complex analysis
, which is the case n = 1 but of a distinct character, these are not just any functions: they are supposed to be analytic
, so that locally speaking they are power series in the variables zi.
Equivalently, as it turns out, they are locally uniform limits of polynomial
s; or locally square-integrable
solutions to the n-dimensional Cauchy–Riemann equations.
, theta functions, and some hypergeometric series
. Naturally also any function of one variable that depends on some complex parameter
is a candidate. The theory, however, for many years didn't become a full-fledged area in mathematical analysis
, since its characteristic phenomena weren't uncovered. The Weierstrass preparation theorem
would now be classed as commutative algebra
; it did justify the local picture, ramification
, that addresses the generalisation of the branch point
s of Riemann surface
theory.
With work of Friedrich Hartogs
, and of Kiyoshi Oka
in the 1930s, a general theory began to emerge; others working in the area at the time were Heinrich Behnke
, Peter Thullen
and Karl Stein
. Hartogs proved some basic results, such as every isolated singularity is removable, for any analytic function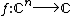
whenever n>1. Naturally the analogues of contour integrals
will be harder to handle: when n = 2 an integral surrounding a point should be over a three-dimensional manifold
(since we are in four real dimensions), while iterating contour (line) integrals over two separate complex variables should come to a double integral over a two-dimensional surface. This means that the residue calculus will have to take a very different character.
After 1945 important work in France, in the seminar of Henri Cartan
, and Germany with Hans Grauert
and Reinhold Remmert
, quickly changed the picture of the theory. A number of issues were clarified, in particular that of analytic continuation
. Here a major difference is evident from the one-variable theory: while for any open connected set D in C we can find a function that will nowhere continue analytically over the boundary, that cannot be said for n > 1. In fact the D of that kind are rather special in nature (a condition called pseudoconvexity). The natural domains of definition of functions, continued to the limit, are called Stein manifold
s and their nature was to make sheaf cohomology
groups vanish. In fact it was the need to put (in particular) the work of Oka on a clearer basis that led quickly to the consistent use of sheaves for the formulation of the theory (with major repercussions for algebraic geometry
, in particular from Grauert's work).
From this point onwards there was a foundational theory, which could be applied to analytic geometry (a name adopted, confusingly, for the geometry of zeroes of analytic functions — this is not the analytic geometry
learned at school), automorphic form
s of several variables, and partial differential equation
s. The deformation theory
of complex structures and complex manifold
s was described in general terms by Kunihiko Kodaira and D.C. Spencer. The celebrated paper GAGA
of Serre
pinned down the crossover point from géometrie analytique to géometrie algébrique.
C.L. Siegel was heard to complain that the new theory of functions of several complex variables had few functions in it — meaning that the special function side of the theory was subordinated to sheaves. The interest for number theory
, certainly, is in specific generalisations of modular form
s. The classical candidates are the Hilbert modular forms and Siegel modular form
s. These days these are associated to algebraic group
s (respectively the Weil restriction
from a totally real number field
of GL(2), and the symplectic group
), for which it happens that automorphic representations can be derived from analytic functions. In a sense this doesn't contradict Siegel; the modern theory has its own, different directions.
Subsequent developments included the hyperfunction
theory, and the edge-of-the-wedge theorem
, both of which had some inspiration from quantum field theory
. There are a number of other fields, such as Banach algebra
theory, that draw on several complex variables.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s of several complex variables is the branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
dealing with functions
- f(z1, z2, ..., zn)
on the space Cn of n-tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. As in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, which is the case n = 1 but of a distinct character, these are not just any functions: they are supposed to be analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
, so that locally speaking they are power series in the variables zi.
Equivalently, as it turns out, they are locally uniform limits of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s; or locally square-integrable
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
solutions to the n-dimensional Cauchy–Riemann equations.
Historical perspective
Many examples of such functions were familiar in nineteenth-century mathematics: abelian functionsAbelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
, theta functions, and some hypergeometric series
Hypergeometric series
In mathematics, a generalized hypergeometric series is a series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by...
. Naturally also any function of one variable that depends on some complex parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
is a candidate. The theory, however, for many years didn't become a full-fledged area in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, since its characteristic phenomena weren't uncovered. The Weierstrass preparation theorem
Weierstrass preparation theorem
In mathematics, the Weierstrass preparation theorem is a tool for dealing with analytic functions of several complex variables, at a given point P...
would now be classed as commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
; it did justify the local picture, ramification
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
, that addresses the generalisation of the branch point
Branch point
In the mathematical field of complex analysis, a branch point of a multi-valued function is a point such that the function is discontinuous when going around an arbitrarily small circuit around this point...
s of Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
theory.
With work of Friedrich Hartogs
Friedrich Hartogs
Friedrich Moritz Hartogs was a German-Jewish mathematician, known for work on set theory and foundational results on several complex variables.- See also :*Hartogs domain*Hartogs–Laurent expansion...
, and of Kiyoshi Oka
Kiyoshi Oka
was a Japanese mathematician who did fundamental work in the theory of several complex variables. He was born in Osaka. He went to Kyoto Imperial University in 1919, turning to mathematics in 1923 and graduating in 1924....
in the 1930s, a general theory began to emerge; others working in the area at the time were Heinrich Behnke
Heinrich Behnke
Heinrich Behnke was a German mathematician and rector at the University of Münster.- Life and career :...
, Peter Thullen
Peter Thullen
Peter Thullen was a German/Ecuadorian mathematician.- Academic Career :He studied under Heinrich Behnke and is noted for work on several complex variables...
and Karl Stein
Karl Stein (mathematician)
Karl Stein was a German mathematician. He is well known for complex analysis and cryptography...
. Hartogs proved some basic results, such as every isolated singularity is removable, for any analytic function
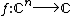whenever n>1. Naturally the analogues of contour integralsLine integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
will be harder to handle: when n = 2 an integral surrounding a point should be over a three-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
(since we are in four real dimensions), while iterating contour (line) integrals over two separate complex variables should come to a double integral over a two-dimensional surface. This means that the residue calculus will have to take a very different character.
After 1945 important work in France, in the seminar of Henri Cartan
Henri Cartan
Henri Paul Cartan was a French mathematician with substantial contributions in algebraic topology. He was the son of the French mathematician Élie Cartan.-Life:...
, and Germany with Hans Grauert
Hans Grauert
Hans Grauert was a German mathematician. He is known for major works on several complex variables, complex manifolds and the application of sheaf theory in this area, which influenced later work in algebraic geometry. Together with Reinhold Remmert he established and developed the theory of...
and Reinhold Remmert
Reinhold Remmert
Reinhold Remmert is a German mathematician born in Osnabrück, Germany. He studied mathematics, mathematical logic and physics in Münster. He established and developed the theory of complex spaces in joint work with Hans Grauert...
, quickly changed the picture of the theory. A number of issues were clarified, in particular that of analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
. Here a major difference is evident from the one-variable theory: while for any open connected set D in C we can find a function that will nowhere continue analytically over the boundary, that cannot be said for n > 1. In fact the D of that kind are rather special in nature (a condition called pseudoconvexity). The natural domains of definition of functions, continued to the limit, are called Stein manifold
Stein manifold
In mathematics, a Stein manifold in the theory of several complex variables and complex manifolds is a complex submanifold of the vector space of n complex dimensions. The name is for Karl Stein.- Definition :...
s and their nature was to make sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
groups vanish. In fact it was the need to put (in particular) the work of Oka on a clearer basis that led quickly to the consistent use of sheaves for the formulation of the theory (with major repercussions for algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, in particular from Grauert's work).
From this point onwards there was a foundational theory, which could be applied to analytic geometry (a name adopted, confusingly, for the geometry of zeroes of analytic functions — this is not the analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
learned at school), automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s of several variables, and partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. The deformation theory
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
of complex structures and complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s was described in general terms by Kunihiko Kodaira and D.C. Spencer. The celebrated paper GAGA
Gaga
- Entertainment :* Lady Gaga , American recording artist* Gaga , a dancing technique* Rara, a type of Caribbean music called Gaga in the Dominican Republic* GNZ-004 Gaga, a mobile weapon in Mobile Suit Gundam 00- Sports :...
of Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
pinned down the crossover point from géometrie analytique to géometrie algébrique.
C.L. Siegel was heard to complain that the new theory of functions of several complex variables had few functions in it — meaning that the special function side of the theory was subordinated to sheaves. The interest for number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, certainly, is in specific generalisations of modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s. The classical candidates are the Hilbert modular forms and Siegel modular form
Siegel modular form
In mathematics, Siegel modular forms are a major type of automorphic form. These stand in relation to the conventional elliptic modular forms as abelian varieties do in relation to elliptic curves; the complex manifolds constructed as in the theory are basic models for what a moduli space for...
s. These days these are associated to algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s (respectively the Weil restriction
Weil restriction
In mathematics, restriction of scalars is a functor which, for any finite extension of fields L/k and any algebraic variety X over L, produces another variety ResL/kX, defined over k...
from a totally real number field
Totally real number field
In number theory, a number field K is called totally real if for each embedding of K into the complex numbers the image lies inside the real numbers...
of GL(2), and the symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
), for which it happens that automorphic representations can be derived from analytic functions. In a sense this doesn't contradict Siegel; the modern theory has its own, different directions.
Subsequent developments included the hyperfunction
Hyperfunction
In mathematics, hyperfunctions are generalizations of functions, as a 'jump' from one holomorphic function to another at a boundary, and can be thought of informally as distributions of infinite order...
theory, and the edge-of-the-wedge theorem
Edge-of-the-wedge theorem
In mathematics, Bogoliubov's edge-of-the-wedge theorem implies that holomorphic functions on two "wedges" with an "edge" in common are analytic continuations of each other provided they both give the same continuous function on the edge. It is used in quantum field theory to construct the...
, both of which had some inspiration from quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. There are a number of other fields, such as Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
theory, that draw on several complex variables.
See also
- Coherent sheafCoherent sheafIn mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
- Cartan's theorems A and BCartan's theorems A and BIn mathematics, Cartan's theorems A and B are two results proved by Henri Cartan around 1951, concerning a coherent sheaf F on a Stein manifold X. They are significant both as applied to several complex variables, and in the general development of sheaf cohomology.Theorem A states that F is spanned...
- Cousin problemsCousin problemsIn mathematics, the Cousin problems are two questions in several complex variables, concerning the existence of meromorphic functions that are specified in terms of local data. They were introduced in special cases by P. Cousin in 1895...
- Hartogs' lemma
- Hartogs' theoremHartogs' theoremIn mathematics, Hartogs' theorem is a fundamental result of Friedrich Hartogs in the theory of several complex variables. Roughly speaking, it states that a 'separately analytic' function is continuous...
- BiholomorphyBiholomorphyIn the mathematical theory of functions of one or more complex variables, and also in complex algebraic geometry, a biholomorphism or biholomorphic function is a bijective holomorphic function whose inverse is also holomorphic....