The triangular function is defined either as:


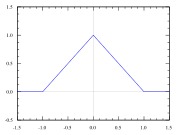
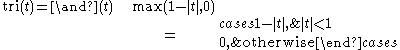
or, equivalently, as the convolution

Convolution

In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...

 of two identical unit rectangular functions:


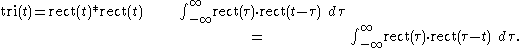
The triangular function can also be represented as the product of the rectangular and absolute value

Absolute value

In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...

 functions:



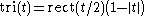
The function is useful in signal processing

Signal processing

Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...

 and communication systems engineering as a representation of an idealized signal, and as a prototype or kernel from which more realistic signals can be derived. It also has applications in pulse code modulation as a pulse shape for transmitting digital signal

Digital signal

A digital signal is a physical signal that is a representation of a sequence of discrete values , for example of an arbitrary bit stream, or of a digitized analog signal...

s and as a matched filter

Matched filter

In telecommunications, a matched filter is obtained by correlating a known signal, or template, with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving the unknown signal with a conjugated time-reversed version of the template...

 for receiving the signals. It is also equivalent to the triangular window sometimes called the Bartlett window.

Scaling

For any parameter,  :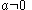

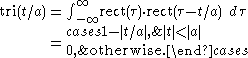
Fourier transform

The transform is easily determined using the convolution property of Fourier transforms and the Fourier transform of the rectangular function: