
Differential entropy
Encyclopedia
Differential entropy is a concept in information theory
that extends the idea of (Shannon) entropy
, a measure of average surprisal of a random variable
, to continuous probability distribution
s.
f whose support
is a set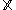 . The differential entropy
. The differential entropy 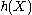 or
or 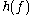 is defined as
is defined as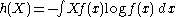 .
.
As with its discrete analog, the units of differential entropy depend on the base of the logarithm
, which is usually 2 (i.e., the units are bit
s). See logarithmic units for logarithms taken in different bases. Related concepts such as joint, conditional
differential entropy, and relative entropy are defined in a similar fashion.
One must take care in trying to apply properties of discrete entropy to differential entropy, since probability density functions can be greater than 1. For example, Uniform
(0,1/2) has negative differential entropy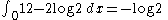 .
.
Thus, differential entropy does not share all properties of discrete entropy.
Note that the continuous mutual information
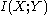 has the distinction of retaining its fundamental significance as a measure of discrete information since it is actually the limit of the discrete mutual information of partitions of X and Y as these partitions become finer and finer. Thus it is invariant under non-linear homeomorphisms (continuous and uniquely invertible maps)
has the distinction of retaining its fundamental significance as a measure of discrete information since it is actually the limit of the discrete mutual information of partitions of X and Y as these partitions become finer and finer. Thus it is invariant under non-linear homeomorphisms (continuous and uniquely invertible maps)
, including linear transformations of X and Y, and still represents the amount of discrete information that can be transmitted over a channel that admits a continuous space of values.
However, differential entropy does not have other desirable properties:
A modification of differential entropy that addresses this is the relative information entropy, also known as the Kullback–Leibler divergence
, which includes an invariant measure
factor (see limiting density of discrete points
).
Let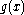 be a Gaussian PDF
be a Gaussian PDF
with mean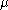 and variance
and variance 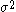 and
and 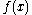 an arbitrary PDF
an arbitrary PDF
with the same variance. Since differential entropy is translation invariant we can assume that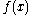 has the same mean of
has the same mean of 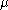 as
as 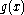 .
.
Consider the Kullback-Leibler divergence between the two distributions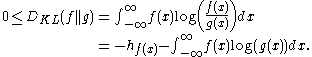
Now note that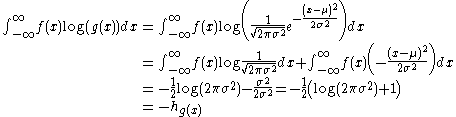
because the result does not depend on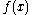 other than through the variance. Combining the two results yields
other than through the variance. Combining the two results yields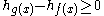
with equality when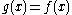 following from the properties of Kullback-Leibler divergence.
following from the properties of Kullback-Leibler divergence.
This result may also be demonstrated using the variational calculus. A Lagrangian function with two Lagrangian multipliers may be defined as:
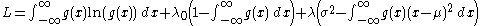
where g(x) is some function with mean μ. When the entropy of g(x) is at a maximum and the constraint equations, which consist of the normalization condition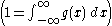 and the requirement of fixed variance
and the requirement of fixed variance 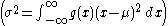 , are both satisfied, then a small variation
, are both satisfied, then a small variation 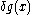 about g(x) will produce a variation
about g(x) will produce a variation 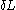 about L which is equal to zero:
about L which is equal to zero:
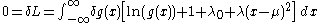
Since this must hold for any small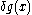 , the term in brackets must be zero, and solving for g(x) yields:
, the term in brackets must be zero, and solving for g(x) yields:
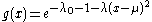
Using the constraint equations to solve for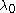 and
and 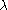 yields the normal distribution:
yields the normal distribution:
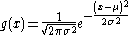
random variable with parameter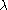 , that is, with probability density function
, that is, with probability density function
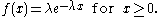
Its differential entropy is then
Here,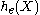 was used rather than
was used rather than 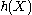 to make it explicit that the logarithm was taken to base e, to simplify the calculation.
to make it explicit that the logarithm was taken to base e, to simplify the calculation.
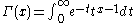 (the gamma function
(the gamma function
),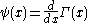 ,
, 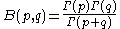 , and
, and 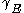 is Euler's constant
is Euler's constant
. Each distribution maximizes the entropy for a particular set of functional constraints listed in the fourth column, and the constraint that x be included in the support of the probability density, which is listed in the fifth column.
(Many of the differential entropies are from .
factor to correct this, (see limiting density of discrete points
). If m(x) is further constrained to be a probability density, the resulting notion is called relative entropy in information theory:
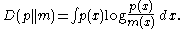
The definition of differential entropy above can be obtained by partitioning the range of X into bins of length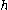 with associated sample points ih within the bins, for X Riemann integrable. This gives a quantized
with associated sample points ih within the bins, for X Riemann integrable. This gives a quantized
version of X, defined by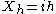 if
if 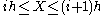 . Then the entropy of
. Then the entropy of 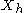 is
is
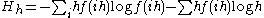 .
.
The first term on the right approximates the differential entropy, while the second term is approximately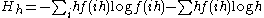 . Note that this procedure suggests that the entropy in the discrete sense of a continuous random variable should be
. Note that this procedure suggests that the entropy in the discrete sense of a continuous random variable should be 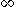 .
.
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
that extends the idea of (Shannon) entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
, a measure of average surprisal of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, to continuous probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s.
Definition
Let X be a random variable with a probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
f whose support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
is a set
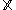 . The differential entropy
. The differential entropy 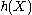 or
or 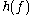 is defined as
is defined as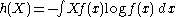 .
.As with its discrete analog, the units of differential entropy depend on the base of the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
, which is usually 2 (i.e., the units are bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s). See logarithmic units for logarithms taken in different bases. Related concepts such as joint, conditional
Conditional entropy
In information theory, the conditional entropy quantifies the remaining entropy of a random variable Y given that the value of another random variable X is known. It is referred to as the entropy of Y conditional on X, and is written H...
differential entropy, and relative entropy are defined in a similar fashion.
One must take care in trying to apply properties of discrete entropy to differential entropy, since probability density functions can be greater than 1. For example, Uniform
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
(0,1/2) has negative differential entropy
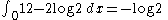 .
.Thus, differential entropy does not share all properties of discrete entropy.
Note that the continuous mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
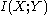 has the distinction of retaining its fundamental significance as a measure of discrete information since it is actually the limit of the discrete mutual information of partitions of X and Y as these partitions become finer and finer. Thus it is invariant under non-linear homeomorphisms (continuous and uniquely invertible maps)
has the distinction of retaining its fundamental significance as a measure of discrete information since it is actually the limit of the discrete mutual information of partitions of X and Y as these partitions become finer and finer. Thus it is invariant under non-linear homeomorphisms (continuous and uniquely invertible maps), including linear transformations of X and Y, and still represents the amount of discrete information that can be transmitted over a channel that admits a continuous space of values.
Properties of differential entropy
- For two densities f and g,
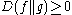 with equality if
with equality if 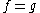 almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
. Similarly, for two random variables X and Y,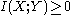 and
and 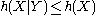 with equality if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
with equality if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
X and Y are independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
. - The chain rule for differential entropy holds as in the discrete case
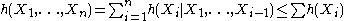 .
. - Differential entropy is translation invariant, ie,
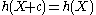 for a constant c.
for a constant c. - Differential entropy is in general not invariant under arbitrary invertible maps. In particular, for a constant a,
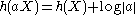 . For a vector valued random variable X and a matrix A,
. For a vector valued random variable X and a matrix A, 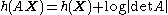 .
. - In general, for a transformation from a random vector X to a random vector with same dimension Y
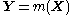 , the corresponding entropies are related via
, the corresponding entropies are related via 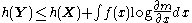 where
where 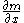 is the Jacobian of the transformation m. Equality is achieved if the transform is bijective, i.e., invertible.
is the Jacobian of the transformation m. Equality is achieved if the transform is bijective, i.e., invertible. - If a random vector
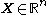 has mean zero and covarianceCovarianceIn probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
has mean zero and covarianceCovarianceIn probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
matrix K,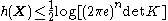 with equality if and only if X is jointly gaussian.
with equality if and only if X is jointly gaussian.
However, differential entropy does not have other desirable properties:
- It is not invariant under change of variablesChange of variablesIn mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with new ones; the new and old variables being related in some specified way...
. - It can be negative.
A modification of differential entropy that addresses this is the relative information entropy, also known as the Kullback–Leibler divergence
Kullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
, which includes an invariant measure
Invariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
factor (see limiting density of discrete points
Limiting density of discrete points
In information theory, the limiting density of discrete points is an adjustment to the formula of Claude Elwood Shannon for differential entropy.It was formulated by Edwin Thompson Jaynes to address defects in the initial definition of differential entropy....
).
Maximization in the normal distribution
With a normal distribution, differential entropy is maximized for a given variance. The following is a proof that a Gaussian variable has the largest entropy amongst all random variables of equal variance.Let
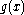 be a Gaussian PDF
be a Gaussian PDFProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
with mean
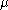 and variance
and variance 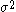 and
and 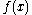 an arbitrary PDF
an arbitrary PDFProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
with the same variance. Since differential entropy is translation invariant we can assume that
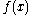 has the same mean of
has the same mean of 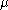 as
as 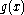 .
.Consider the Kullback-Leibler divergence between the two distributions
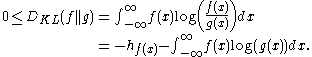
Now note that
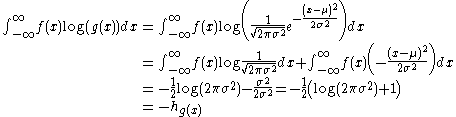
because the result does not depend on
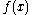 other than through the variance. Combining the two results yields
other than through the variance. Combining the two results yields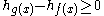
with equality when
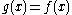 following from the properties of Kullback-Leibler divergence.
following from the properties of Kullback-Leibler divergence.This result may also be demonstrated using the variational calculus. A Lagrangian function with two Lagrangian multipliers may be defined as:
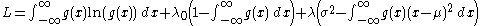
where g(x) is some function with mean μ. When the entropy of g(x) is at a maximum and the constraint equations, which consist of the normalization condition
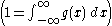 and the requirement of fixed variance
and the requirement of fixed variance 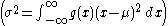 , are both satisfied, then a small variation
, are both satisfied, then a small variation 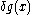 about g(x) will produce a variation
about g(x) will produce a variation 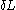 about L which is equal to zero:
about L which is equal to zero: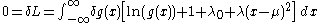
Since this must hold for any small
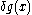 , the term in brackets must be zero, and solving for g(x) yields:
, the term in brackets must be zero, and solving for g(x) yields: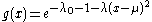
Using the constraint equations to solve for
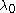 and
and 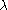 yields the normal distribution:
yields the normal distribution: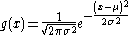
Example: Exponential distribution
Let X be an exponentially distributedExponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
random variable with parameter
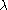 , that is, with probability density function
, that is, with probability density function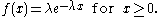
Its differential entropy is then
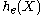 |
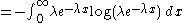 |
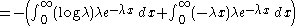 |
|
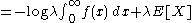 |
|
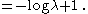 |
Here,
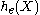 was used rather than
was used rather than 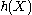 to make it explicit that the logarithm was taken to base e, to simplify the calculation.
to make it explicit that the logarithm was taken to base e, to simplify the calculation.Differential entropies for various distributions
In the table below,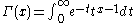 (the gamma function
(the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
),
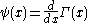 ,
, 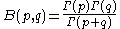 , and
, and 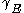 is Euler's constant
is Euler's constantEuler-Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
. Each distribution maximizes the entropy for a particular set of functional constraints listed in the fourth column, and the constraint that x be included in the support of the probability density, which is listed in the fifth column.
| Distribution Name | Probability density function (pdf) | Entropy in nats | Maximum Entropy Constraint | Support |
|---|---|---|---|---|
| Uniform Uniform distribution (continuous) In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by... |
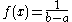 |
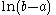 |
None | 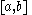 |
| Normal | 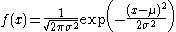 |
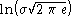 |
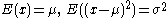 |
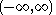 |
| Exponential Exponential distribution In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e... |
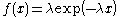 |
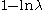 |
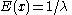 |
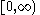 |
| Rayleigh | 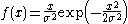 |
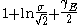 |
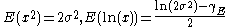 |
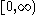 |
| Beta | 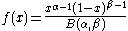 for for 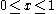 |
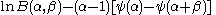 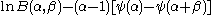 |
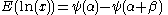 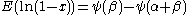 |
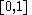 |
| Cauchy Cauchy distribution The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner... |
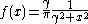 |
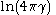 |
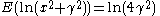 |
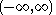 |
| Chi | 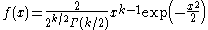 |
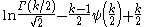 |
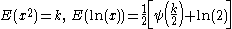 |
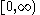 |
| Chi-squared | 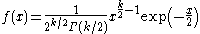 |
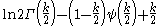 |
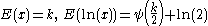 |
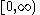 |
| Erlang | 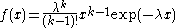 |
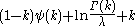 |
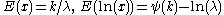 |
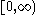 |
| F | 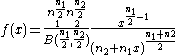 |
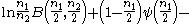 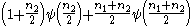 |
 |
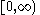 |
| Gamma | 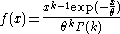 |
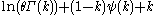 |
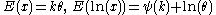 |
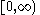 |
| Laplace | 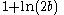 |
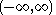 |
||
| Logistic | 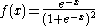 |
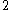 |
 |
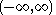 |
| Lognormal | 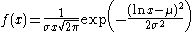 |
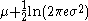 |
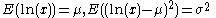 |
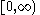 |
| Maxwell-Boltzmann | 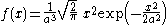 |
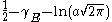 |
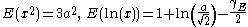 |
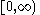 |
| Generalized normal | 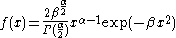 |
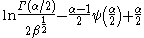 |
 |
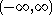 |
| Pareto | 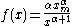 |
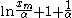 |
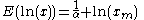 |
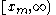 |
| Student's t | 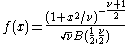 |
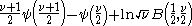 |
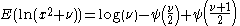 |
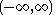 |
| Triangular | 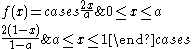 |
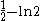 |
 |
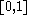 |
| Weibull | 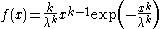 |
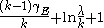 |
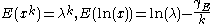 |
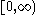 |
| Multivariate normal | 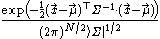 |
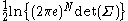 |
 |
 |
(Many of the differential entropies are from .
Variants
As described above, differential entropy does not share all properties of discrete entropy. A modification of differential entropy adds an invariant measureInvariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
factor to correct this, (see limiting density of discrete points
Limiting density of discrete points
In information theory, the limiting density of discrete points is an adjustment to the formula of Claude Elwood Shannon for differential entropy.It was formulated by Edwin Thompson Jaynes to address defects in the initial definition of differential entropy....
). If m(x) is further constrained to be a probability density, the resulting notion is called relative entropy in information theory:
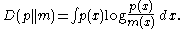
The definition of differential entropy above can be obtained by partitioning the range of X into bins of length
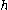 with associated sample points ih within the bins, for X Riemann integrable. This gives a quantized
with associated sample points ih within the bins, for X Riemann integrable. This gives a quantizedQuantization (signal processing)
Quantization, in mathematics and digital signal processing, is the process of mapping a large set of input values to a smaller set – such as rounding values to some unit of precision. A device or algorithmic function that performs quantization is called a quantizer. The error introduced by...
version of X, defined by
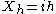 if
if 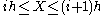 . Then the entropy of
. Then the entropy of 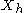 is
is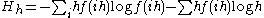 .
.The first term on the right approximates the differential entropy, while the second term is approximately
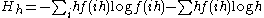 . Note that this procedure suggests that the entropy in the discrete sense of a continuous random variable should be
. Note that this procedure suggests that the entropy in the discrete sense of a continuous random variable should be 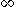 .
.See also
- Information entropyInformation entropyIn information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
- Information theoryInformation theoryInformation theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
- Limiting density of discrete pointsLimiting density of discrete pointsIn information theory, the limiting density of discrete points is an adjustment to the formula of Claude Elwood Shannon for differential entropy.It was formulated by Edwin Thompson Jaynes to address defects in the initial definition of differential entropy....
- Self-informationSelf-informationIn information theory, self-information is a measure of the information content associated with the outcome of a random variable. It is expressed in a unit of information, for example bits,nats,or...
- Kullback-Leibler divergence
- Entropy estimationEntropy estimationEstimating the differential entropy of a system or process, given some observations, is useful in various science/engineering applications, such as Independent Component Analysis, image analysis, genetic analysis, speech recognition, manifold learning, and time delay estimation...

