Logistic distribution
Encyclopedia
In probability theory
and statistics
, the logistic distribution is a continuous probability distribution.
Its cumulative distribution function
is the logistic function
, which appears in logistic regression
and feedforward neural networks.
It resembles the normal distribution in shape but has heavier tails (higher kurtosis
).
(cdf), which is an instance of the family of logistic functions:

In this equation, x is the random variable
, μ is the mean
, and s is a parameter proportional to the standard deviation
.
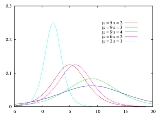
(pdf) of the logistic distribution is given by:

Because the pdf can be expressed in terms of the square of the hyperbolic secant function
"sech", it is sometimes referred to as the sech-square(d) distribution.
cumulative distribution function of the logistic distribution is , a generalization of the logit
, a generalization of the logit
function, defined as follows:

 . This yields the following density function:
. This yields the following density function:

Both the United States Chess Federation
and FIDE have switched their formulas for calculating chess ratings from the normal distribution to the logistic distribution; see Elo rating system
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the logistic distribution is a continuous probability distribution.
Its cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
is the logistic function
Logistic function
A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
, which appears in logistic regression
Logistic regression
In statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
and feedforward neural networks.
It resembles the normal distribution in shape but has heavier tails (higher kurtosis
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
).
Cumulative distribution function
The logistic distribution receives its name from its cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
(cdf), which is an instance of the family of logistic functions:

In this equation, x is the random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, μ is the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
, and s is a parameter proportional to the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
.
Probability density function
The probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(pdf) of the logistic distribution is given by:

Because the pdf can be expressed in terms of the square of the hyperbolic secant function
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
"sech", it is sometimes referred to as the sech-square(d) distribution.
- See also: hyperbolic secant distribution
Quantile function
The inverseInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
cumulative distribution function of the logistic distribution is
 , a generalization of the logit
, a generalization of the logitLogit
The logit function is the inverse of the sigmoidal "logistic" function used in mathematics, especially in statistics.Log-odds and logit are synonyms.-Definition:The logit of a number p between 0 and 1 is given by the formula:...
function, defined as follows:

Alternative parameterization
An alternative parameterization of the logistic distribution, in terms of the variance σ2, can be derived using the substitution . This yields the following density function:
. This yields the following density function:
Applications
The logistic distribution and the S-shaped pattern that results from it have been extensively used in many different areas, including:- Biology – to describe how species populations grow in competition
- Epidemiology – to describe the spreading of epidemics
- Psychology – to describe learning
- Technology – to describe how new technologies diffuse and substitute for each other
- Marketing – the diffusion of new-product sales
- Energy – the diffusion and substitution of primary energy sources, as in the Hubbert curveHubbert curveThe Hubbert curve is an approximation of the production rate of a resource over time. It is a symmetric logistic distribution curve, often confused with the "normal" gaussian function. It first appeared in "Nuclear Energy and the Fossil Fuels," geophysicist M...
- Hydrology - In hydrologyHydrologyHydrology is the study of the movement, distribution, and quality of water on Earth and other planets, including the hydrologic cycle, water resources and environmental watershed sustainability...
the distribution of long duration river discharge and rainfall (e.g. monthly and yearly totals, consisting of the sum of 30 respectively 360 daily values) is often thought to be almost normal according to the central limit theoremCentral limit theoremIn probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
. The normal distribution, however, needs a numeric approximation. As the logistic distribution, which can be solved analytically, is similar to the normal distribution, it can be used instead. The blue picture illustrates an example of fitting the logistic distribution to ranked October rainfalls - that are almost normally distributed - and it shows the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of the cumulative frequency analysisCumulative frequency analysisCumulative frequency analysis is the applcation of estimation theory to exceedance probability . The complement, the non-exceedance probability concerns the frequency of occurrence of values of a phenomenon staying below a reference value. The phenomenon may be time or space dependent...
. - Physics - the cdf of this distribution describes a Fermi gasFermi gasA Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
and more specifically the number of electrons within a metal that can be expected to occupy a given quantum state. Its range is between 0 and 1, reflecting the Pauli exclusion principlePauli exclusion principleThe Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
. The value is given as a function of the kinetic energy corresponding to that state and is parametrized by the Fermi energyFermi energyThe Fermi energy is a concept in quantum mechanics usually referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature....
and also the temperature (and Boltzmann constant). By changing the sign in front of the "1" in the denominator, one goes from Fermi–Dirac statistics to Bose–Einstein statisticsBose–Einstein statisticsIn statistical mechanics, Bose–Einstein statistics determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.-Concept:...
. In this case, the expected number of particles (bosons) in a given state can exceed unity, which is indeed the case for systems such as lasers.
Both the United States Chess Federation
United States Chess Federation
The United States Chess Federation is a non-profit organization, the governing chess organization within the United States, and one of the federations of the FIDE. The USCF was founded in 1939 from the merger of two regional chess organizations, and grew gradually until 1972, when membership...
and FIDE have switched their formulas for calculating chess ratings from the normal distribution to the logistic distribution; see Elo rating system
Elo rating system
The Elo rating system is a method for calculating the relative skill levels of players in two-player games such as chess. It is named after its creator Arpad Elo, a Hungarian-born American physics professor....
.
Related distributions
- If
 then
then 
- Logistic distribution mimics Sech distribution
- If
 (Uniform distribution (continuous)Uniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
(Uniform distribution (continuous)Uniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
) then
- If
 (Exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
(Exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
) then
- If
 and
and  then
then 
- If
 and
and  (Gumbel distribution) then
(Gumbel distribution) then 
- If
 and
and  (Generalized extreme value distribution) then
(Generalized extreme value distribution) then 
- If
 and
and  then
then 
- If
 then
then  (log-logistic distributionLog-logistic distributionIn probability and statistics, the log-logistic distribution is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events whose rate increases initially and decreases later, for example mortality from cancer following...
(log-logistic distributionLog-logistic distributionIn probability and statistics, the log-logistic distribution is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events whose rate increases initially and decreases later, for example mortality from cancer following...
) and (shifted log-logistic distribution)
(shifted log-logistic distribution)
Higher order moments
The n-th order central moment can be expressed in terms of the quantile function:-

This integral is well-known and can be expressed in terms of Bernoulli numberBernoulli numberIn mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s:-

See also
- Generalized logistic distributionGeneralized logistic distributionThe term generalized logistic distribution is used as the name for several different families of probability distributions. For example, Johnson et al. list four forms, which are listed below. One family described here has also been called the skew-logistic distribution...
- Logistic regressionLogistic regressionIn statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
- Sigmoid functionSigmoid functionMany natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...
- Generalized logistic distribution
-



