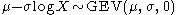Generalized extreme value distribution
Encyclopedia
In probability theory
and statistics
, the generalized extreme value (GEV) distribution is a family of continuous probability distribution
s developed within extreme value theory
to combine the Gumbel, Fréchet and Weibull families also known as type I, II and III extreme value distributions. By the extreme value theorem the GEV distribution is the limit distribution of properly normalized maxima of a sequence of independent and identically distributed random variables. Because of this, the GEV distribution is used as an approximation to model the maxima of long (finite) sequences of random variables.
In some fields of application the generalized extreme value distribution is known as the Fisher–Tippett distribution, named after R. A. Fisher and L. H. C. Tippett who recognised three function forms outlined below. However usage of this name is sometimes restricted to mean the special case of the Gumbel distribution.
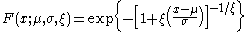
for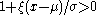
, where 
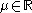is the location parameter, 
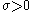the scale parameter and 
the shape parameter.
The density function is, consequently
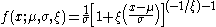
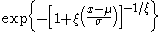
again, for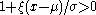
.
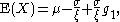
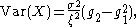
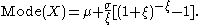
The skewness
is for ξ>0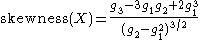
For ξ<0, the sign of the numerator is reversed.
The excess kurtosis
is: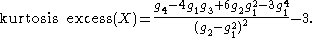
where
, k=1,2,3,4, and 
is the gamma function
.
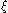governs the tail behaviour of the distribution. The sub-families defined by 
, 
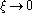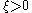and 
correspond, respectively, to the Gumbel, Fréchet and Weibull families, whose cumulative distribution functions are displayed below.
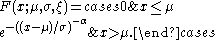
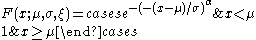
where
.
Remark I: The theory here relates to maxima and the distribution being discussed is an extreme value distribution for maxima. A Generalised Extreme Value distribution for minima can be obtained, for example by substituting (-x) for x in the distribution function, and subtracting from one: this yields a separate family of distributions.
Remark II: The ordinary Weibull distribution arises in reliability applications and is obtained from the distribution here by using the variable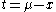
, which gives a strictly positive support - in contrast to the use in the extreme value theory here. This arises because the Weibull distribution is used in cases that deal with the minimum rather than the maximum. The distribution here has an addition parameter compared to the usual form of the Weibull distribution and, in addition, is reversed so that the distribution has an upper bound rather than a lower bound. Importantly, in applications of the GEV, the upper bound is unknown and so must be estimated while when applying the Weibull distribution the lower bound is known to be zero.
Remark III: Note the differences in the ranges of interest for the three extreme value distributions: Gumbel is unlimited, Fréchet has a lower limit, while the reversed Weibull has an upper limit.
One can link the type I to types II and III the following way: if the cumulative distribution function of some random variable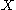
is of type II: 
, then the cumulative distribution function of 
is of type I, namely 
. Similarly, if the cumulative distribution function of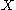 
is of type III: 
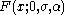, the cumulative distribution function of 
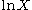is of type I: 
.
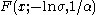of generalized extreme value distribution solves the stability postulate
equation. The generalized extreme value distribution is a special case of a max-stable distribution, and is a transformation of a min-stable distribution.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the generalized extreme value (GEV) distribution is a family of continuous probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s developed within extreme value theory
Extreme value theory
Extreme value theory is a branch of statistics dealing with the extreme deviations from the median of probability distributions. The general theory sets out to assess the type of probability distributions generated by processes...
to combine the Gumbel, Fréchet and Weibull families also known as type I, II and III extreme value distributions. By the extreme value theorem the GEV distribution is the limit distribution of properly normalized maxima of a sequence of independent and identically distributed random variables. Because of this, the GEV distribution is used as an approximation to model the maxima of long (finite) sequences of random variables.
In some fields of application the generalized extreme value distribution is known as the Fisher–Tippett distribution, named after R. A. Fisher and L. H. C. Tippett who recognised three function forms outlined below. However usage of this name is sometimes restricted to mean the special case of the Gumbel distribution.
Specification
The generalized extreme value distribution has cumulative distribution function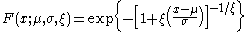for
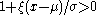, where 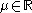is the location parameter, 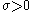the scale parameter and the shape parameter.The density function is, consequently
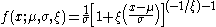
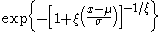
again, for
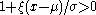.Summary Statistics
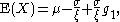
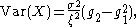
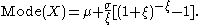
Some simple statistics of the distribution are:The skewness
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
is for ξ>0
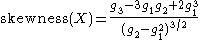
For ξ<0, the sign of the numerator is reversed.
The excess kurtosis
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
is:
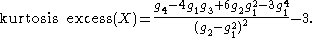
where
, k=1,2,3,4, and is the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
Link to Fréchet, Weibull and Gumbel families
The shape parameter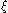 governs the tail behaviour of the distribution. The sub-families defined by 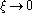, 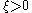and correspond, respectively, to the Gumbel, Fréchet and Weibull families, whose cumulative distribution functions are displayed below.
- Gumbel or type I extreme value distribution
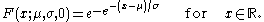
- Fréchet or type II extreme value distribution, if ξ=α-1 with
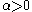
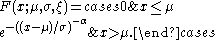
- Reversed Weibull or type III extreme value distribution, if ξ=−α-1, with
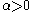
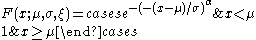
where
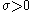.Remark I: The theory here relates to maxima and the distribution being discussed is an extreme value distribution for maxima. A Generalised Extreme Value distribution for minima can be obtained, for example by substituting (-x) for x in the distribution function, and subtracting from one: this yields a separate family of distributions.
Remark II: The ordinary Weibull distribution arises in reliability applications and is obtained from the distribution here by using the variable
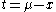, which gives a strictly positive support - in contrast to the use in the extreme value theory here. This arises because the Weibull distribution is used in cases that deal with the minimum rather than the maximum. The distribution here has an addition parameter compared to the usual form of the Weibull distribution and, in addition, is reversed so that the distribution has an upper bound rather than a lower bound. Importantly, in applications of the GEV, the upper bound is unknown and so must be estimated while when applying the Weibull distribution the lower bound is known to be zero.Remark III: Note the differences in the ranges of interest for the three extreme value distributions: Gumbel is unlimited, Fréchet has a lower limit, while the reversed Weibull has an upper limit.
One can link the type I to types II and III the following way: if the cumulative distribution function of some random variable
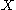is of type II: , then the cumulative distribution function of is of type I, namely . Similarly, if the cumulative distribution function of 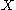is of type III: 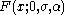, the cumulative distribution function of 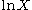is of type I: 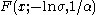.Properties
The cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of generalized extreme value distribution solves the stability postulate
Stability postulate
In probability theory, to obtain a nondegenerate limiting distribution of the extreme value distribution, it is necessary to "reduce" the actual greatest value by applying a linear transformation with coefficients that depend on the sample size....
equation. The generalized extreme value distribution is a special case of a max-stable distribution, and is a transformation of a min-stable distribution.
Related distributions
- If
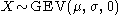then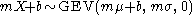 
- If
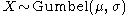(Gumbel distribution) then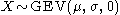 
- If
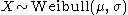(Weibull distribution) then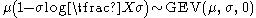 
- If
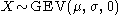then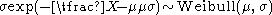 
(Weibull distribution) - If
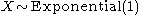(Exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
) then