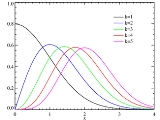
Chi distribution
Encyclopedia
In probability theory
and statistics
, the chi distribution is a continuous probability distribution
. It is the distribution of the square root of the sum of squares of independent random variables having a standard normal distribution. The most familiar example is the Maxwell distribution of (normalized) molecular speeds which is a chi distribution with 3 degrees of freedom (one for each spatial coordinate). If
are k independent, normally distributed random variables with means 
and standard deviation
s
, then the statistic
is distributed according to the chi distribution. The chi distribution has one parameter:
which specifies the number of degrees of freedom
(i.e. the number of
).
where
is the Gamma function
.
where
is the regularized Gamma function.
is given by:
where again,
is Kummer's confluent hypergeometric function
.
are then given by:
where
is the Gamma function
. The first few raw moments are:
where the rightmost expressions are derived using the recurrence relationship for the Gamma function:
From these expressions we may derive the following relationships:
Mean:
Variance:
Skewness:
Kurtosis excess:
where
is the polygamma function.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the chi distribution is a continuous probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. It is the distribution of the square root of the sum of squares of independent random variables having a standard normal distribution. The most familiar example is the Maxwell distribution of (normalized) molecular speeds which is a chi distribution with 3 degrees of freedom (one for each spatial coordinate). If
are k independent, normally distributed random variables with means and standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
s
, then the statisticis distributed according to the chi distribution. The chi distribution has one parameter:
which specifies the number of degrees of freedomDegrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
(i.e. the number of
).Probability density function
The probability density function iswhere
is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
Cumulative distribution function
The cumulative distribution function is given by:where
is the regularized Gamma function.Moment generating function
The moment generating function is given by:Characteristic function
The characteristic functionCharacteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
is given by:
where again,
is Kummer's confluent hypergeometric functionConfluent hypergeometric function
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
.
Moments
The raw momentsMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
are then given by:
where
is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. The first few raw moments are:
where the rightmost expressions are derived using the recurrence relationship for the Gamma function:
From these expressions we may derive the following relationships:
Mean:
Variance:
Skewness:
Kurtosis excess:
Entropy
The entropy is given by:where
is the polygamma function.Related distributions
- If
then 
(chi-squared distribution) 
(normal distribution)- If
then 
(half-normal distributionHalf-normal distributionThe half-normal distribution is the probability distribution of the absolute value of a random variable that is normally distributed with expected value 0 and variance σ2. I.e...
) for any
(Rayleigh distribution)
(Maxwell distribution)
(The normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of n standard normally distributed variables is a chi distribution with k degrees of freedomDegrees of freedomDegrees of freedom can mean:* Degrees of freedom , independent displacements and/or rotations that specify the orientation of the body or system...
)- chi distribution is a special case of the generalized gamma distributionGeneralized gamma distributionThe generalized gamma distribution is a continuous probability distribution with three parameters. It is a generalization of the two-parameter gamma distribution...
| Name | Statistic |
|---|---|
| chi-squared distribution |  |
| noncentral chi-squared distribution |  |
| chi distribution |  |
| noncentral chi distribution |  |
External links
- http://mathworld.wolfram.com/ChiDistribution.html