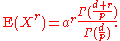Generalized gamma distribution
Encyclopedia
The generalized gamma distribution is a continuous probability distribution
with three parameters. It is a generalization of the two-parameter gamma distribution. Since many distributions commonly used for parametric models in survival analysis
(such as the Weibull distribution and the log-normal distribution) are special cases of the generalized gamma, it is sometimes used to determine which parametric model is appropriate for a given set of data.
, 
, and 
. For non-negative x, the probability density function
of the generalized gamma is
where
denotes the gamma function
.
The cumulative distribution function
is
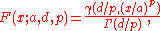
where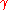
denotes the lower incomplete gamma function
.
If
then the generalized gamma distribution becomes the Weibull distribution. Alternatively, if 
the generalised gamma becomes the gamma distribution.
Alternative parameterisations of this distribution are sometimes used; for example with the substitution α = d/p. In addition, a shift parameter can be added, so the domain of x starts at some value other than zero.
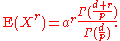
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
with three parameters. It is a generalization of the two-parameter gamma distribution. Since many distributions commonly used for parametric models in survival analysis
Survival analysis
Survival analysis is a branch of statistics which deals with death in biological organisms and failure in mechanical systems. This topic is called reliability theory or reliability analysis in engineering, and duration analysis or duration modeling in economics or sociology...
(such as the Weibull distribution and the log-normal distribution) are special cases of the generalized gamma, it is sometimes used to determine which parametric model is appropriate for a given set of data.
Characteristics
The generalized gamma has three parameters:, , and . For non-negative x, the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the generalized gamma is
where
denotes the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
The cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
is
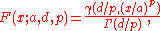
where
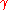denotes the lower incomplete gamma functionIncomplete gamma function
In mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
.
If
then the generalized gamma distribution becomes the Weibull distribution. Alternatively, if the generalised gamma becomes the gamma distribution.Alternative parameterisations of this distribution are sometimes used; for example with the substitution α = d/p. In addition, a shift parameter can be added, so the domain of x starts at some value other than zero.
Moments
If X has a generalized gamma distribution as above, then