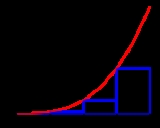
Riemann sum
Encyclopedia

In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
. It may
also be used to define the integration operation. The method was named after German mathematician Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
.
Definition
Let f: D → R be a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
defined on a subset D of the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R. Let I = [a, b] be a closed interval contained in D, and let P = {
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of I, where a = x0 < x1 < x2 ... < xn = b.
The Riemann sum of f over I with partition P is defined as
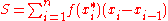
where xi-1 ≤ x*i ≤ xi. The choice of x*i in this interval is arbitrary. If x*i = xi-1 for all i, then S is called a left Riemann sum. If x*i = xi, then S is called a right Riemann sum. If x*i = (xi+xi-1)/2, then S is called a middle Riemann sum. The average of the left and right Riemann sum is the trapezoidal sum.
If it is given that
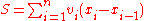
where vi is the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of f over [xi-1, xi], then S is defined to be an upper Riemann sum. Similarly, if vi is the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of f over [xi−1, xi], then S is a lower Riemann sum.
Any Riemann sum on a given partition (that is, for any choice of x*i between xi-1 and xi) is contained between the lower and the upper Riemann sums. A function is defined to be Riemann integrable
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
if the lower and upper Riemann sums get ever closer as the partition gets finer and finer. This fact can also be used for numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
.
Methods
The four methods of Riemann summation are usually best approached with partitions of equal size. The interval is therefore divided into
is therefore divided into  subintervals, each of length
subintervals, each of length 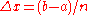 . The points in the partition will then be
. The points in the partition will then be-
 .
.
Left sum
For the left Riemann sum, approximating the function by its value at the left-end point gives multiple rectangles with base Δx and height f(a + iΔx). Doing this for i = 0, 1, ..., n−1, and adding up the resulting areas gives
The left Riemann sum amounts to an overestimation if f is monotonically decreasing on this interval, and an underestimation if it is monotonically increasing.
Right sum
f is here approximated by the value at the right endpoint. This gives multiple rectangles with base and height . Doing this for
. Doing this for  , and adding up the resulting areas produces
, and adding up the resulting areas produces
The right Riemann sum amounts to an overestimation if
 is monotonically increasing, and an underestimation if it is monotonically decreasing.
is monotonically increasing, and an underestimation if it is monotonically decreasing.Middle sum
Approximating f at the midpoint of intervals gives f(a + Q/2) for the first interval, for the next one f(a + 3Q/2), and so on until f(b-Q/2). Summing up the areas gives
The error of this formula will be
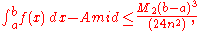
where
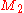 is the maximum value of the absolute value
is the maximum value of the absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of
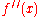 on the interval.
on the interval.Trapezoidal rule
In this case, the values of the function f on an interval are approximated by the average of the values at the left and right endpoints. In the same manner as above, a simple calculation using the area formula for a trapezium
for a trapeziumTrapezoid
In Euclidean geometry, a convex quadrilateral with one pair of parallel sides is referred to as a trapezoid in American English and as a trapezium in English outside North America. A trapezoid with vertices ABCD is denoted...
with parallel sides b1, b2 and height h produces
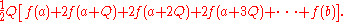

where
 is the maximum value of the absolute value of
is the maximum value of the absolute value of 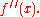
Example
Taking an example, the area under the curve of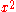 between 0 and 2 can be procedurally computed using Riemann's method.
between 0 and 2 can be procedurally computed using Riemann's method.The interval from 0 to 2 is firstly divided into n subintervals, each of which is given a width of
 ; these are the widths of the Riemann rectangles. Because the right Riemann sum is to be used, the sequence of x coordinates for the boxes will be
; these are the widths of the Riemann rectangles. Because the right Riemann sum is to be used, the sequence of x coordinates for the boxes will be  . Therefore, the sequence of the heights of the boxes will be
. Therefore, the sequence of the heights of the boxes will be 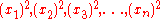 . It is an important fact that
. It is an important fact that 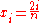 , and
, and 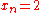 .
.The area of each box will be
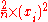 and therefore the nth right Riemann sum will be:
and therefore the nth right Riemann sum will be: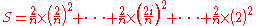 .
.Hence:


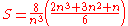

If the limit is viewed as
 , it can be concluded that the approximation approaches the actual value of the area under the curve as the number of boxes increases. Hence:
, it can be concluded that the approximation approaches the actual value of the area under the curve as the number of boxes increases. Hence: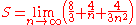
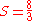
This method agrees with the definite integral as calculated in more mechanical ways:
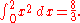
See also
- Riemann integralRiemann integralIn the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
- Riemann–Stieltjes integral
- Lebesgue integral
- Simpson's ruleSimpson's ruleIn numerical analysis, Simpson's rule is a method for numerical integration, the numerical approximation of definite integrals. Specifically, it is the following approximation:...

