In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, an eigenfunction of a linear operator, A, defined on some function space

Function space

In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...

 is any non-zero function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has


for some scalar

Scalar (mathematics)

In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....

, λ, the corresponding eigenvalue. The solution of the differential eigenvalue problem also depends on any boundary conditions required of . In each case there are only certain eigenvalues 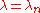(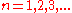) that admit a corresponding solution for 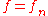(with each 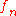belonging to the eigenvalue 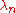) when combined with the boundary conditions. The existence of eigenfunctions is typically the most insightful way to analyze .

For example, 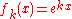is an eigenfunction for the differential operator

Differential operator

In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...

for any value of 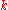, with corresponding eigenvalue 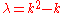. If boundary conditions are applied to this system (e.g., at two physical locations in space), then only certain values of satisfy the boundary conditions, generating corresponding discrete eigenvalues .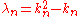

Specifically, in the study of signals and systems

LTI system theory

Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...

, the eigenfunction of a system is the signal 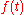which when input into the system, produces a response with the complex constant .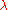

Applications

Eigenfunctions play an important role in many branches of physics. An important example is quantum mechanics

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

, where the Schrödinger equation

Schrödinger equation

The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....

,

with

has solutions of the form


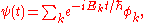
where 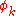are eigenfunctions of the operator with eigenvalues . The fact that only certain eigenvalues with associated eigenfunctions 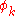satisfy Schrödinger's equation leads to a natural basis for quantum mechanics and the periodic table of the elements, with each an allowable energy state of the system. The success of this equation in explaining the spectral characteristics of hydrogen is considered one of the great triumphs of 20th century physics.

Due to the nature of the Hamiltonian

Hamiltonian (quantum mechanics)

In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...

 operator , its eigenfunctions are orthogonal functions

Orthogonal functions

In mathematics, two functions f and g are called orthogonal if their inner product \langle f,g\rangle is zero for f ≠ g. Whether or not two particular functions are orthogonal depends on how their inner product has been defined. A typical definition of an inner product for functions is...

. This is not necessarily the case for eigenfunctions of other operators (such as the example mentioned above). Orthogonal functions 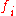, have the property that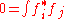


where 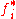is the complex conjugate

Complex conjugate

In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...

 of

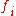
whenever , in which case the set is said to be orthogonal. Also, it is linearly independent

Linear independence

In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...

.

See also

• Eigenvalue, eigenvector and eigenspace
  Eigenvalue, eigenvector and eigenspace
  The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
  
  
• Hilbert–Schmidt theorem
• Spectral theory of ordinary differential equations
  Spectral theory of ordinary differential equations
  In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation...
  
  
• Fixed point combinator
  Fixed point combinator
  In computer science, a fixed-point combinator is a higher-order function that computes a fixed point of other functions. A fixed point of a function f is a value x such that x = f. For example, 0 and 1 are fixed points of the function f = x2, because 0 = 02 and 1 = 12...