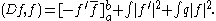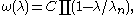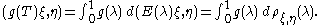Spectral theory of ordinary differential equations
Encyclopedia
In mathematics
, the spectral theory of ordinary differential equations is the part of spectral theory
concerned with the determination of the spectrum and eigenfunction expansion
associated with a linear ordinary differential equation
. In his dissertation Hermann Weyl
generalized the classical Sturm–Liouville theory on a finite closed interval to second order differential operator
s with singularities at the endpoints of the interval, possibly semi-infinite or infinite. Unlike the classical case, the spectrum may no longer consist of just a countable set of eigenvalues, but may also contain a continuous part. In this case the eigenfunction expansion involves an integral over the continuous part with respect to a spectral measure
, given by the Titchmarsh–Kodaira formula. The theory was put in its final simplified form for singular differential equations of even degree by Kodaira and others, using von Neumann
's spectral theorem
. It has had important applications in quantum mechanics
, operator theory
and harmonic analysis
on semisimple Lie groups.
for second order ordinary differential equations on a compact interval was developed by Jacques Charles François Sturm and Joseph Liouville
in the nineteenth century and is now known as Sturm–Liouville theory. In modern language it is an application of the spectral theorem
for compact operator
s due to David Hilbert
. In his dissertation, published in 1910, Hermann Weyl
extended this theory to second order ordinary differential equations with
singularities at the endpoints of the interval, now allowed to be infinite or semi-infinite. He simultaneously developed a spectral theory adapted to these special operators and introduced boundary conditions in terms of his celebrated dichotomy between limit points and limit circles.
In the 1920s John von Neumann
established a general spectral theorem for unbounded
self-adjoint operator
s, which Kunihiko Kodaira used to streamline Weyl's method. Kodaira also generalised Weyl's method to singular ordinary differential equations of even order and obtained a simple formula for the spectral measure
. The same formula had also been obtained independently by E. C. Titchmarsh in 1946 (scientific communication between Japan
and the United Kingdom
had been interrupted by World War II
). Titchmarsh had followed the method of the German mathematician Emil Hilb
, who derived the eigenfunction expansions using complex function theory instead of operator theory
. Other methods avoiding the spectral theorem were later developed independently by Levitan, Levinson and Yoshida, who used the fact that the resolvent
of the singular differential operator could be approximated by compact
resolvents corresponding to Sturm–Liouville problems for proper subintervals. Another method was found by Mark Grigoryevich Krein
; his use of direction functionals was subsequently generalised by I. M. Glazman to arbitrary ordinary differential equations of even order.
Weyl applied his theory to Carl Friedrich Gauss
's hypergeometric differential equation
, thus obtaining a far-reaching generalisation of the transform formula of Gustav Ferdinand Mehler
(1881) for the Legendre differential equation
, rediscovered by the Russian physicist Vladimir Fock
in 1943, and usually called the Mehler–Fock transform. The corresponding ordinary differential operator is the radial part of the Laplacian operator on 2-dimensional hyperbolic space
. More generally, the Plancherel theorem
for SL(2,R) of Harish Chandra and Gelfand–Naimark can be deduced from Weyl's theory for the hypergeometric equation, as can the theory of spherical function
s for the isometry group
s of higher dimensional hyperbolic spaces. Harish Chandra's later development of the Plancherel theorem for general real semisimple Lie groups was strongly influenced by the methods Weyl developed for eigenfunction expansions associated with singular ordinary differential equations. Equally importantly the theory also laid the mathematical foundations for the analysis of the Schrödinger equation
and scattering matrix in quantum mechanics
.
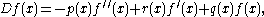
where p is a strictly positive continuously differentiable function and q and r are continuous
real-valued functions.
For x0 in (a, b), define the Liouville transformation ψ by
Let U be the unitary operator
(Uf)·ψ ψ'½ = f from L2 (a,b) onto
L2(c,d), where c = ψ(a) and d = ψ(b). Then
where Q·ψ = q and R·ψ= (p' /2 + r)/p½.
The term in g' can be removed using an Euler integrating factor
. If S' /S = −R/2, then h = Sg
satisfies
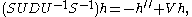
where the potential
V is given by V = Q + S2/2 + S' /2.
The differential operator can thus always be reduced to one of the form
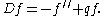
for second order differential equations with values in a
Banach space
E.
Let α, β be arbitrary elements of E, A a bounded operator
on E and q a continuous function on [a,b].
Then, for c = a or b,
the differential equation
has a unique solution f in C2([a,b],E) satisfying the initial conditions
In fact a solution of the differential equation with these initial conditions is equivalent to a solution
of the integral equation
with T the bounded linear map on C([a,b], E) defined by
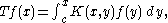
where K is the Volterra kernel
and
Since ||Tk|| tends to 0, this integral equation has a unique solution given by the Neumann series
This iterative scheme is often called Picard iteration after the French mathematician Charles Émile Picard
.
of L with eigenvalue λ.
W(f, g) is defined by
Green's formula states that for x, y in (a, b)
When q is continuous and f, g C2 on the compact interval [a, b], this formula also holds for x = a or y = b.
When f and g are eigenfunctions for the same eigenvalue, then
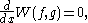
so that W(f, g) is independent of x.
space of C2 functions f on [a, b] satisfying the mixed boundary conditions
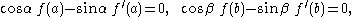
with inner product
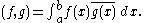
In practise usually one of the two unmixed boundary conditions:
is imposed at each endpoint c = a, b.
The differential operator D given by
acts on H0. A function f in H0 is called an eigenfunction
of D (for the above choice of boundary values) if Df = λ f for some complex number λ, the corresponding eigenvalue.
By Green's formula, D is formally self-adjoint
on H0:
= (f, Dg) for f, g in H0.
As a consequence, exactly as for a self-adjoint matrix in finite dimensions,
It turns out that the eigenvalues can be described by the maximum-minimum
principle of Rayleigh
–Ritz
(see below). In fact it is easy to see a priori that the eigenvalues are bounded below because the operator D is itself bounded below on H0:
In fact integrating by parts
For unmixed boundary conditions, the first term vanishes and the inequality holds with M = inf q.
In the mixed case the first term can be estimated using an elementary Peter-Paul version of Sobolev's inequality
:
In fact, since
only an estimate for f(b) is needed and this follows by replacing f(x) in the above inequality by (x − a)n·(b − a)−n·f(x) for n sufficiently large.
which at each point, together with their first derivatives, depend holomorphically on λ. Let
an entire holomorphic function
.
This function ω(λ) plays the rôle of the characteristic polynomial
of D. Indeed the uniqueness of the fundamental eigenfunctions implies that its zeros are precisely the eigenvalues of D and that each non-zero eigenspace is one-dimensional. In particular there are at most countably many eigenvalues of D and, if there are infinitely many, they must tend to infinity. It turns out that the zeros of ω(λ) also have mutilplicity one (see below).
If λ is not an eigenvalue of D on H0, define the Green's function
by
This kernel defines an operator on the inner product space C[a,b] via
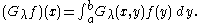
Since Gλ(x,y) is continuous on [a, b] x [a, b], it defines a Hilbert–Schmidt operator on the Hilbert space completion
H of C[a, b] = H1 (or equivalently of the dense subspace H0), taking values in H1. This operator carries H1 into H0. When λ is real, Gλ(x,y) = Gλ(y,x) is also real, so defines a self-adjoint operator on H. Moreover
Thus the operator Gλ can be identified with the resolvent
(D − λ)−1.
The corresponding normalised eigenfunctions form an orthonormal basis of H0.
The kth eigenvalue of D is given by the minimax principle
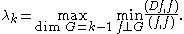
In particular if q1 ≤ q2, then
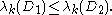
In fact let T = Gλ for λ large and negative. Then T defines a compact self-adjoint operator
on the Hilbert space H.
By the spectral theorem
for compact self-adjoint operators, H has an orthonormal basis consisting of eigenvectors ψn of T with
Tψn = μn ψn, where μn tends to zero. The range of T contains H0 so is dense. Hence 0 is not an eigenvector of T. The resolvent properties of T imply that ψn lies in H0 and that
The minimax principle follows because if
then λ(G)= λk for the linear span
of the first k − 1 eigenfunctions. For any other (k − 1)-dimensional subspace G, some f in the linear span of the first k eigenvectors must be orthogonal to G. Hence λ(G) ≤ (Df,f)/(f,f) ≤ λk.
The minimax principle shows that
It follows that the resolvent (D − λ)−1 is a trace-class operator
whenever λ is not an eigenvalue of D and hence that the Fredholm determinant
det I − μ(D − λ)−1 is defined.
The Dirichlet boundary conditions imply that
Using Picard iteration, Titchmarsh showed that φλ(b), and hence ω(λ),
is an entire function of finite order
1/2:
At a zero μ of ω(λ),
φμ(b) = 0. Moreover
satisfies (D − μ)ψ = φμ. Thus
This implies that
For otherwise ψ(b) = 0, so that ψ would have to lie in H0.
But then
= ((D − μ)ψ, φμ) = (ψ, (D − μ)φμ) = 0,
a contradiction.
On the other hand the distribution of the zeros of the entire function
ω(λ) is already known from the minimax principle.
By the Hadamard factorization theorem, it follows
that
for some non-zero constant C.
Hence
In particular if 0 is not an eigenvalue of D
on a closed interval [a, b] is a complex-valued function such that
its total variation
V(ρ), the supremum
of the variations
over all dissection
s
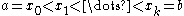
is finite. The real and imaginary parts of ρ are real-valued functions of bounded variation. If ρ is real-valued and normalised so that ρ(a)=0,
it has a canonical decomposition as the difference of two bounded non-decreasing functions:
where ρ+(x) and ρ–(x) are the total positive and negative variation of ρ over [a, x].
If f is a continuous function on [a, b] its Riemann–Stieltjes integral with respect to ρ
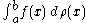
is defined to be the limit of approximating sums
as the mesh
of the dissection, given by sup |xr+1 - xr|, tends to zero.
This integral satisfies
and thus defines a bounded linear functional dρ on C[a, b] with norm
||dρ||=V(ρ).
Every bounded linear functional μ on C[a, b] has an absolute value
|μ| defined for non-negative f by
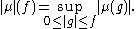
The form |μ| extends linearly to a bounded linear form on C[a, b] with norm ||μ|| and satisfies the characterizing inequality
for f in C[a, b]. If μ is real, i.e. is real-valued on real-valued functions, then
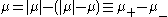
gives a canonical decomposition as a difference of positive forms, i.e. forms that are non-negative on non-negative functions.
Every positive form μ extends uniquely to the linear span of non-negative bounded lower semicontinuous functions g by the formula
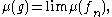
where the non-negative continuous functions fn increase pointwise to g.
The same therefore applies to an arbitrary bounded linear form μ, so that a function ρ of bounded variation may be defined by
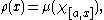
where χA denotes the characteristic function
of a subset A of [a, b]. Thus μ = dρ and ||μ|| = ||dρ||.
Moreover μ+ = dρ+ and μ– = dρ–.
This correspondence between functions of bounded variation and bounded linear forms is a special case of the Riesz representation theorem
.
The support
of μ = dρ is the complement of all points x in [a,b] where ρ is constant on some neighborhood of x; by definition it is a closed subset A of [a,b]. Moreover μ((1-χA)f) =0, so that μ(f) = 0 if f vanishes on A.
on H with 0 ≤ T ≤ I, so that the spectrum
σ(T) of T is contained in [0,1]. If p(t) is a complex polynomial, then by the spectral mapping theorem
and hence
where ||·||∞ denotes the uniform norm on C[0,1]. By the Weierstrass approximation theorem, polynomials are uniformly dense in C[0, 1]. It follows that f(T) can be defined for every f in C[0,1], with
If 0 ≤ g ≤ 1 is a lower semicontinuous function on [0,1], for example the characteristic function χ[0,α] of a subinterval of [0,1], then
g is a pointwise increasing limit of non-negative fn in C[0,1].
According to Sz.-Nagy
, if ξ is a vector in H, then the vectors
form a Cauchy sequence
in H, since, for n ≥ m,
and (ηn,ξ) = (fn(T)ξ, ξ) is bounded and increasing, so has a limit.
It follows that g(T) can be defined by
If ξ and η are vectors in H, then
defines a bounded linear form μξ,η on H. By the Riesz representation theorem
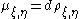
for a unique normalised function ρξ,η of bounded variation on [0,1].
dρξ,η (or sometimes slightly incorrectly ρξ,η itself) is called the spectral measure
determined by ξ and η.
The operator g(T) is accordingly uniquely characterised by the equation
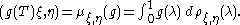
The spectral projection
E(λ) is defined by
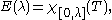
so that
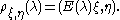
It follows that
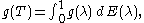
which is understood in the sense that for any vectors ξ and η,
For a single vector ξ, μξ = μξ,ξ is a positive form on [0,1]
(in other words proportional to a probability measure
on [0,1]) and ρξ = ρξ,ξ is non-negative and non-decreasing.
Polarisation shows that all the forms μξ,η can naturally be expressed in terms of such positive forms, since
If the vector ξ is such that the linear span
of the vectors (Tnξ) is dense in H, i.e. ξ is a cyclic vector for
T, then the map U defined by
satisfies
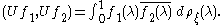
Let L2([0,1], dρξ) denote the Hilbert space completion of C[0,1] associated
with the possibly degenerate inner product on the right hand side.
Thus U extends to a unitary transformation
of L2([0,1], dρξ) onto H. UTU* is then just multiplication by λ on L2([0,1], dρξ); and more generally Uf(T)U* is multiplication by f(λ). In this case, the support of dρξ
is exactly σ(T), so that
on an open interval (a, b) requires an initial analysis of the behaviour of the fundamental
eigenfunctions near the endpoints a and b to determine possible boundary conditions there.
Unlike the regular Sturm–Liouville case, in some circumstances spectral values
of D can have multiplicity
2. In the development outlined below standard assumptions will be imposed on p and q that guarantee that the spectrum of
D has multiplicity one everywhere and is bounded below.
This includes almost all important applications; modifications required for the more general case will be discussed later.
Having chosen the boundary conditions, as in the classical theory the resolvent of D, (D + R )−1 for R large and positive, is
given by an operator T corresponding to a Green's function constructed from two fundamental eigenfunctions.
In the classical case T was a compact self-adjoint operator; in this case T is just a self-adjoint bounded operator with 0 ≤ T ≤ I.
The abstract theory of spectral measure can therefore be applied to T to give the eigenfunction expansion for D.
The central idea in the proof of Weyl and Kodaira can be explained informally as follows. Assume that the spectrum of D lies in [1,∞) and that T =D−1 and let
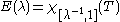
be the spectral projection of D corresponding to the interval [1,λ]. For an arbitrary function f define
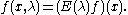
f(x,λ) may be regarded as a differentiable map into the space of functions of bounded variation ρ; or equivalently as a differentiable map
into the Banach space E of bounded linear functionals dρ on C[α,β] whenever [α,β] is a compact subinterval of [1, ∞).
Weyl's fundamental observation was that dλ f satisfies a second order ordinary differential equation taking values in E:
After imposing initial conditions on the first two derivatives at a fixed point c, this equation can be solved explicitly
in terms of the two fundamental eigenfunctions and the "initial value" functionals
This point of view may now be turned on its head: f(c,λ) and fx(c,λ) may be written as
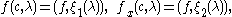
where ξ1(λ) and ξ2(λ) are given purely in terms of the fundamental eigenfunctions.
The functions of bounded variation
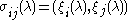
determine a spectral measure on the spectrum of D and can be computed explicitly from the behaviour
of the fundamental eigenfunctions (the Titchmarsh–Kodaira formula).
and let D be the second order differential operator
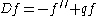
on (0,∞). Fix a point c in (0,∞) and, for λ complex, let φλ, χλ be the unique fundamental eigenfunctions of D on (0,∞) satisfying
together with the initial conditions at c
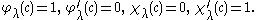
Then their Wronskian satisfies
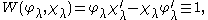
since it is constant and equal to 1 at c.
If λ is non-real and 0 < x < ∞, then Green's formula implies
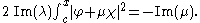
This defines a circle
in the complex μ-plane, the interior
of which is given by
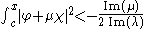
if x > c and by
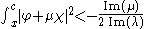
if x < c.
Let Dx be the closed disc enclosed by the circle. By definition
these closed discs are nested and decrease as x approaches 0 or ∞. So in the limit, the circles
tend either to a limit circle or a limit point at each end. In particular if μ is a
limit point or a point on the limit circle at 0 or ∞, then |φ + μχ|2 is
square integrable (L2) near 0 or ∞. In particular:
On the other hand if Dg = λ' g for another value λ', then
satisfies Dh = λh, so that
Using this to estimate g, it follows that
More generally if Dg= (λ – r) g for some function r(x), then
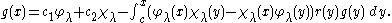
From this it follows that
so that in particular
Similarly
so that in particular
Many more elaborate criteria to be limit point or limit circle can be found in the mathematical literature.
on (0,∞) with q0 positive and continuous on (0,∞) and p0 continuously differentiable in [0,∞), positive in (0,∞) and p0(0)=0.
Moreover assume that after reduction to standard form
D0 becomes the equivalent operator
on (0,∞) where q has a finite limit at ∞. Thus
At 0, D may be either limit circle or limit point. In either case there is an eigenfunction Φ0 with DΦ0=0 and Φ0 square integrable near 0. In the limit circle case, Φ0 determines a boundary condition at 0:
For λ complex, let Φλ and Χλ satisfy
Let
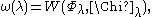
a constant which vanishes precisely when Φλ and Χλ are proportional, i.e. λ is an eigenvalue of D for these boundary conditions.
On the other hand, this cannot occur if Im λ ≠ 0 or if λ is negative.
Indeed if D f= λf with q0 – λ ≥ δ >0, then by Green's formula (Df,f) = (f,Df), since W(f,f*) is constant. So λ must be real. If f is taken to be real-valued in the D0 realization, then for 0 < x < y
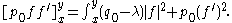
Since p0(0) = 0 and f is integrable near 0, p0f f ' must vanish at 0. Setting x = 0, it follows that f(y) f '(y) >0, so that f2 is increasing, contradicting the square integrability of f near ∞.
Thus, adding a positive scalar to q, it may be assumed that
If ω(λ) ≠ 0, the Green's function
Gλ(x,y) at λ is defined by
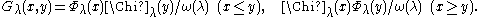
and is independent of the choice of λ and Χλ.
In the examples there will be a third "bad" eigenfunction Ψλ defined and holomorphic for λ not in [1, ∞) such that
Ψλ satisfies the boundary conditions at neither 0 nor ∞. This means that for λ not in [1, ∞)
In this case Χλ is proportional to Φλ + m(λ) Ψλ, where
Let H1 be the space of square integrable continuous functions on (0,∞) and let H0 be
Define T = G0 by
Then T D = I on H0, D T = I on H1 and the operator D is bounded below on H0:
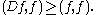
Thus T is a self-adjoint bounded operator with 0 ≤ T ≤ I.
Formally T = D−1. The corresponding operators Gλ defined for λ not in [1,∞) can be formally identified with
and satisfy Gλ (D – λ) = I on H0, (D – λ)Gλ = I on H1.
ψψ
Then ρ(λ) is a lower semicontinuous non-decreasing function of λ and if
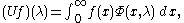
then U defines a unitary transformation of L2(0,∞) onto L2([1,∞), dρ) such that
UDU−1 corresponds to multiplication by λ.
The inverse transformation U−1 is given by
The spectrum of D equals the support of dρ.
Kodaira gave a streamlined version of Weyl's original proof. (M.H. Stone
had previously shown how part of Weyl's work could be simplified using von Neumann's spectral theorem.)
In fact for T =D−1 with 0 ≤ T ≤ I, the spectral projection E(λ) of T is defined by
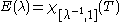
It is also the spectral projection of D corresponding to the interval [1,λ].
For f in H1 define
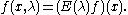
f(x,λ) may be regarded as a differentiable map into the space of functions ρ of bounded variation; or equivalently as a differentiable map
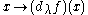
into the Banach space E of bounded linear functionals dρ on C[α,β] for any compact subinterval [α,β] of [1, ∞).
The functionals (or measures) dλ f(x) satisfies the following E-valued second order ordinary differential equation:
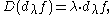
with initial conditions at c in (0,∞)
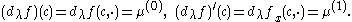
If φλ and χλ are the special eigenfunctions adapted to c, then
Moreover
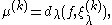
where
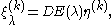
with
(As the notation suggests, ξλ(0) and ξλ(1) do not depend on the choice of z.)
Setting
it follows that
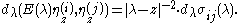
On the other hand there are holomorphic functions
a(λ), b(λ) such that
Since W(φλ,χλ) = 1, the Green's function is given by
Direct calculation shows that
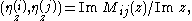
where the so-called characteristic matrix Mij(z) is given by
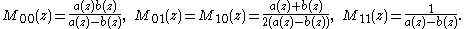
Hence
which immediately implies
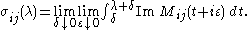
(This is a special case of the "Stietljes inversion formula".)
Setting ψλ(0)=φλ and ψλ(1)=χλ, it follows that
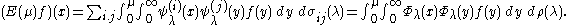
This identity is equivalent to the spectral theorem and Titchmarsh–Kodaira formula.
D
on (1,∞). The eigenfunctions are the Legendre function
s
with eigenvalue λ ≥ 0. The two Mehler–Fock transformations are
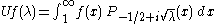
and
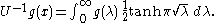
(Often this is written in terms of the variable τ = √λ.)
Mehler and Fock studied this differential operator because it arose as the radial component of the Laplacian on 2-dimensional hyperbolic space.
More generally, consider the group G = SU(1,1) consisting of complex matrices of the form
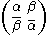
with determinant |α|2 − |β|2 = 1.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the spectral theory of ordinary differential equations is the part of spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
concerned with the determination of the spectrum and eigenfunction expansion
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
associated with a linear ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
. In his dissertation Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
generalized the classical Sturm–Liouville theory on a finite closed interval to second order differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s with singularities at the endpoints of the interval, possibly semi-infinite or infinite. Unlike the classical case, the spectrum may no longer consist of just a countable set of eigenvalues, but may also contain a continuous part. In this case the eigenfunction expansion involves an integral over the continuous part with respect to a spectral measure
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
, given by the Titchmarsh–Kodaira formula. The theory was put in its final simplified form for singular differential equations of even degree by Kodaira and others, using von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
's spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
. It has had important applications in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
and harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
on semisimple Lie groups.
Introduction
Spectral theorySpectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
for second order ordinary differential equations on a compact interval was developed by Jacques Charles François Sturm and Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
in the nineteenth century and is now known as Sturm–Liouville theory. In modern language it is an application of the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
for compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
s due to David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
. In his dissertation, published in 1910, Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
extended this theory to second order ordinary differential equations with
singularities at the endpoints of the interval, now allowed to be infinite or semi-infinite. He simultaneously developed a spectral theory adapted to these special operators and introduced boundary conditions in terms of his celebrated dichotomy between limit points and limit circles.
In the 1920s John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
established a general spectral theorem for unbounded
Unbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s, which Kunihiko Kodaira used to streamline Weyl's method. Kodaira also generalised Weyl's method to singular ordinary differential equations of even order and obtained a simple formula for the spectral measure
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
. The same formula had also been obtained independently by E. C. Titchmarsh in 1946 (scientific communication between Japan
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
and the United Kingdom
United Kingdom
The United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
had been interrupted by World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
). Titchmarsh had followed the method of the German mathematician Emil Hilb
Emil Hilb
Emil Hilb was a German-Jewish mathematician who worked in the fields of special functions, differential equations, and difference equations...
, who derived the eigenfunction expansions using complex function theory instead of operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
. Other methods avoiding the spectral theorem were later developed independently by Levitan, Levinson and Yoshida, who used the fact that the resolvent
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
of the singular differential operator could be approximated by compact
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
resolvents corresponding to Sturm–Liouville problems for proper subintervals. Another method was found by Mark Grigoryevich Krein
Mark Grigoryevich Krein
Mark Grigorievich Krein was a Soviet Jewish mathematician, one of the major figures of the Soviet school of functional analysis. He is known for works in operator theory , the problem of moments, classical analysis and representation theory.He was born in Kiev, leaving home at age 17 to go to...
; his use of direction functionals was subsequently generalised by I. M. Glazman to arbitrary ordinary differential equations of even order.
Weyl applied his theory to Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
's hypergeometric differential equation
Hypergeometric differential equation
In mathematics, the Gaussian or ordinary hypergeometric function 2F1 is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation...
, thus obtaining a far-reaching generalisation of the transform formula of Gustav Ferdinand Mehler
Gustav Ferdinand Mehler
Gustav Ferdinand Mehler, or Ferdinand Gustav Mehler was a German mathematician, who introduced Mehler's formula, Mehler–Fock formula, Mehler–Heine formula, Mehler functions....
(1881) for the Legendre differential equation
Legendre function
In mathematics, the Legendre functions Pλ, Qλ and associated Legendre functions P, Q are generalizations of Legendre polynomials to non-integer degree.-Differential equation:...
, rediscovered by the Russian physicist Vladimir Fock
Vladimir Fock
Vladimir Aleksandrovich Fock was a Soviet physicist, who did foundational work on quantum mechanics and quantum electrodynamics....
in 1943, and usually called the Mehler–Fock transform. The corresponding ordinary differential operator is the radial part of the Laplacian operator on 2-dimensional hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
. More generally, the Plancherel theorem
Plancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
for SL(2,R) of Harish Chandra and Gelfand–Naimark can be deduced from Weyl's theory for the hypergeometric equation, as can the theory of spherical function
Spherical function
Spherical function can refer to* Spherical harmonics*Zonal spherical function...
s for the isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
s of higher dimensional hyperbolic spaces. Harish Chandra's later development of the Plancherel theorem for general real semisimple Lie groups was strongly influenced by the methods Weyl developed for eigenfunction expansions associated with singular ordinary differential equations. Equally importantly the theory also laid the mathematical foundations for the analysis of the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
and scattering matrix in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
Reduction to standard form
Let D be the second order differential operator on (a,b) given by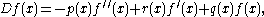where p is a strictly positive continuously differentiable function and q and r are continuous
real-valued functions.
For x0 in (a, b), define the Liouville transformation ψ by
Let U be the unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
(Uf)·ψ ψ'½ = f from L2 (a,b) onto
L2(c,d), where c = ψ(a) and d = ψ(b). Then
where Q·ψ = q and R·ψ= (p' /2 + r)/p½.
The term in g' can be removed using an Euler integrating factor
Integrating factor
In mathematics, an integrating factor is a function that is chosen to facilitate the solving of a given equation involving differentials. It is commonly used to solve ordinary differential equations, but is also used within multivariable calculus, in this case often multiplying through by an...
. If S' /S = −R/2, then h = Sg
satisfies
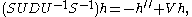
where the potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
V is given by V = Q + S2/2 + S' /2.
The differential operator can thus always be reduced to one of the form
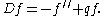
Existence theorem
The following is a version of the classical Picard existence theoremPicard–Lindelöf theorem
In mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
for second order differential equations with values in a
Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
E.
Let α, β be arbitrary elements of E, A a bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
on E and q a continuous function on [a,b].
Then, for c = a or b,
the differential equation
- Df = Af
has a unique solution f in C2([a,b],E) satisfying the initial conditions
- f(c) = β, f '(c) = α.
In fact a solution of the differential equation with these initial conditions is equivalent to a solution
of the integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
- f = h + T f
with T the bounded linear map on C([a,b], E) defined by
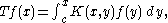
where K is the Volterra kernel
- K(x,t)= (x − t)(q(t) − A)
and
- h(x) = α(x − c) + β.
Since ||Tk|| tends to 0, this integral equation has a unique solution given by the Neumann series
- f = (I − T)−1 h = h + T h + T2 h + T3 h + ···
This iterative scheme is often called Picard iteration after the French mathematician Charles Émile Picard
Charles Émile Picard
Charles Émile Picard FRS was a French mathematician. He was elected the fifteenth member to occupy seat 1 of the Académie Française in 1924.- Biography :...
.
Fundamental eigenfunctions
If f is twice continuously differentiable (i.e. C2) on (a, b) satisfying Df = λf, then f is called an eigenfunctionEigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
of L with eigenvalue λ.
- In the case of a compact interval [a, b] and q continuous on [a, b], the existence theorem implies that for c = a or b and every complex number λ there a unique C2 eigenfunction fλ on [a, b] with fλ(c) and f 'λ(c) prescribed. Moreover, for each x in [a, b], fλ(x) and f 'λ(x) are holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s of λ.
- For an arbitrary interval (a,b) and q continuous on (a, b), the existence theorem implies that for c in (a, b) and every complex number λ there a unique C2 eigenfunction fλ on (a, b) with fλ(c) and f 'λ(c) prescribed. Moreover, for each x in (a, b), fλ(x) and f 'λ(x) are holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s of λ.
Green's formula
If f and g are C2 functions on (a, b), the WronskianWronskian
In mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...
W(f, g) is defined by
- W(f, g) (x) = f(x) g '(x) − f '(x) g(x).
Green's formula states that for x, y in (a, b)
When q is continuous and f, g C2 on the compact interval [a, b], this formula also holds for x = a or y = b.
When f and g are eigenfunctions for the same eigenvalue, then
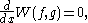
so that W(f, g) is independent of x.
Classical Sturm–Liouville theory
Let [a, b] be a finite closed interval, q a real-valued continuous function on [a, b] and let H0 be thespace of C2 functions f on [a, b] satisfying the mixed boundary conditions
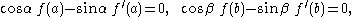
with inner product
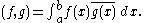
In practise usually one of the two unmixed boundary conditions:
- Dirichlet boundary conditionDirichlet boundary conditionIn mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
f(c) = 0 - Neumann boundary conditionNeumann boundary conditionIn mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
f '(c) = 0
is imposed at each endpoint c = a, b.
The differential operator D given by
acts on H0. A function f in H0 is called an eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
of D (for the above choice of boundary values) if Df = λ f for some complex number λ, the corresponding eigenvalue.
By Green's formula, D is formally self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
on H0:
= (f, Dg) for f, g in H0.
As a consequence, exactly as for a self-adjoint matrix in finite dimensions,
- the eigenvalues of D are real;
- the eigenspaces for distinct eigenvalues are orthogonal.
It turns out that the eigenvalues can be described by the maximum-minimum
Courant minimax principle
In mathematics, the Courant minimax principle gives the eigenvalues of a real symmetric matrix. It is named after Richard Courant.-Introduction:The Courant minimax principle gives a condition for finding the eigenvalues for a real symmetric matrix...
principle of Rayleigh
John Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
–Ritz
Walter Ritz
Walther Ritz was a Swiss theoretical physicist.His father, Raphael Ritz, a native of Valais, was a well-known landscape and interior scenes artist. His mother was the daughter of the engineer Noerdlinger of Tübingen. Ritz studied in Zurich and Göttingen...
(see below). In fact it is easy to see a priori that the eigenvalues are bounded below because the operator D is itself bounded below on H0:
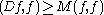for some finite constant 
.
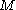In fact integrating by parts
For unmixed boundary conditions, the first term vanishes and the inequality holds with M = inf q.
In the mixed case the first term can be estimated using an elementary Peter-Paul version of Sobolev's inequality
Sobolev inequality
In mathematics, there is in mathematical analysis a class of Sobolev inequalities, relating norms including those of Sobolev spaces. These are used to prove the Sobolev embedding theorem, giving inclusions between certain Sobolev spaces, and the Rellich–Kondrachov theorem showing that under...
:
-
- "Given ε > 0, there is constant R >0 such that |f(x)|2 ≤ ε (f', f') + R (f, f) for all f in C1[a, b]."
In fact, since
-
- |f(b) − f(x)| ≤ (b − a)½·||f '||2,
only an estimate for f(b) is needed and this follows by replacing f(x) in the above inequality by (x − a)n·(b − a)−n·f(x) for n sufficiently large.
Green's function (regular case)
From the theory of ordinary differential equations, there are unique fundamental eigenfunctions φλ(x), χλ(x) such that- D φλ = λ φλ, φλ(a) = sin α, φλ'(a) = cos α
- D χλ = λ χλ, χλ(b) = sin β, χλ'(b) = cos β
which at each point, together with their first derivatives, depend holomorphically on λ. Let
- ω(λ) = W(φλ, χλ),
an entire holomorphic function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
.
This function ω(λ) plays the rôle of the characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of D. Indeed the uniqueness of the fundamental eigenfunctions implies that its zeros are precisely the eigenvalues of D and that each non-zero eigenspace is one-dimensional. In particular there are at most countably many eigenvalues of D and, if there are infinitely many, they must tend to infinity. It turns out that the zeros of ω(λ) also have mutilplicity one (see below).
If λ is not an eigenvalue of D on H0, define the Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
by
- Gλ(x,y) = φλ (x) χλ(y) / ω(λ) for x ≥ y and χλ(x) φλ (y) / ω(λ) for y ≥ x.
This kernel defines an operator on the inner product space C[a,b] via
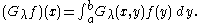
Since Gλ(x,y) is continuous on [a, b] x [a, b], it defines a Hilbert–Schmidt operator on the Hilbert space completion
H of C[a, b] = H1 (or equivalently of the dense subspace H0), taking values in H1. This operator carries H1 into H0. When λ is real, Gλ(x,y) = Gλ(y,x) is also real, so defines a self-adjoint operator on H. Moreover
- Gλ (D − λ) =I on H0
- Gλ carries H1 into H0, and (D − λ) Gλ = I on H1.
Thus the operator Gλ can be identified with the resolvent
Resolvent formalism
In mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....
(D − λ)−1.
Spectral theorem
Theorem. The eigenvalues of D are real of multiplicity one and form an increasing sequence λ1 < λ2 < ··· tending to infinity.The corresponding normalised eigenfunctions form an orthonormal basis of H0.
The kth eigenvalue of D is given by the minimax principle
Courant minimax principle
In mathematics, the Courant minimax principle gives the eigenvalues of a real symmetric matrix. It is named after Richard Courant.-Introduction:The Courant minimax principle gives a condition for finding the eigenvalues for a real symmetric matrix...
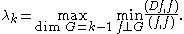
In particular if q1 ≤ q2, then
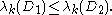
In fact let T = Gλ for λ large and negative. Then T defines a compact self-adjoint operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
on the Hilbert space H.
By the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
for compact self-adjoint operators, H has an orthonormal basis consisting of eigenvectors ψn of T with
Tψn = μn ψn, where μn tends to zero. The range of T contains H0 so is dense. Hence 0 is not an eigenvector of T. The resolvent properties of T imply that ψn lies in H0 and that
- D ψn = (λ + 1/μn) ψn
The minimax principle follows because if
then λ(G)= λk for the linear span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
of the first k − 1 eigenfunctions. For any other (k − 1)-dimensional subspace G, some f in the linear span of the first k eigenvectors must be orthogonal to G. Hence λ(G) ≤ (Df,f)/(f,f) ≤ λk.
Wronskian as a Fredholm determinant
For simplicity, suppose that m ≤ q(x) ≤ M on [0,π] with Dirichlet boundary conditions.The minimax principle shows that
It follows that the resolvent (D − λ)−1 is a trace-class operator
whenever λ is not an eigenvalue of D and hence that the Fredholm determinant
Fredholm determinant
In mathematics, the Fredholm determinant is a complex-valued function which generalizes the determinant of a matrix. It is defined for bounded operators on a Hilbert space which differ from the identity operator by a trace-class operator...
det I − μ(D − λ)−1 is defined.
The Dirichlet boundary conditions imply that
- ω(λ)= φλ(b).
Using Picard iteration, Titchmarsh showed that φλ(b), and hence ω(λ),
is an entire function of finite order
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
1/2:
- ω(λ) = O(e√|λ|)
At a zero μ of ω(λ),
φμ(b) = 0. Moreover
satisfies (D − μ)ψ = φμ. Thus
- ω(λ) = (λ − μ)ψ(b) + O( (λ − μ)2).
This implies that
- μ is a simple zero of ω(λ).
For otherwise ψ(b) = 0, so that ψ would have to lie in H0.
But then
= ((D − μ)ψ, φμ) = (ψ, (D − μ)φμ) = 0,
a contradiction.
On the other hand the distribution of the zeros of the entire function
ω(λ) is already known from the minimax principle.
By the Hadamard factorization theorem, it follows
that
for some non-zero constant C.
Hence
In particular if 0 is not an eigenvalue of D
Functions of bounded variation
A function ρ(x) of bounded variationBounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
on a closed interval [a, b] is a complex-valued function such that
its total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
V(ρ), the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of the variations
over all dissection
Partition of an interval
In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
s
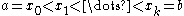
is finite. The real and imaginary parts of ρ are real-valued functions of bounded variation. If ρ is real-valued and normalised so that ρ(a)=0,
it has a canonical decomposition as the difference of two bounded non-decreasing functions:
where ρ+(x) and ρ–(x) are the total positive and negative variation of ρ over [a, x].
If f is a continuous function on [a, b] its Riemann–Stieltjes integral with respect to ρ
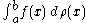
is defined to be the limit of approximating sums
as the mesh
Partition of an interval
In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
of the dissection, given by sup |xr+1 - xr|, tends to zero.
This integral satisfies
and thus defines a bounded linear functional dρ on C[a, b] with norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
||dρ||=V(ρ).
Every bounded linear functional μ on C[a, b] has an absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
|μ| defined for non-negative f by
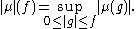
The form |μ| extends linearly to a bounded linear form on C[a, b] with norm ||μ|| and satisfies the characterizing inequality
- |μ(f)| ≤ |μ|(|f|)
for f in C[a, b]. If μ is real, i.e. is real-valued on real-valued functions, then
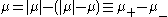
gives a canonical decomposition as a difference of positive forms, i.e. forms that are non-negative on non-negative functions.
Every positive form μ extends uniquely to the linear span of non-negative bounded lower semicontinuous functions g by the formula
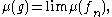
where the non-negative continuous functions fn increase pointwise to g.
The same therefore applies to an arbitrary bounded linear form μ, so that a function ρ of bounded variation may be defined by
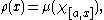
where χA denotes the characteristic function
Characteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
of a subset A of [a, b]. Thus μ = dρ and ||μ|| = ||dρ||.
Moreover μ+ = dρ+ and μ– = dρ–.
This correspondence between functions of bounded variation and bounded linear forms is a special case of the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
.
The support
Support (measure theory)
In mathematics, the support of a measure μ on a measurable topological space is a precise notion of where in the space X the measure "lives"...
of μ = dρ is the complement of all points x in [a,b] where ρ is constant on some neighborhood of x; by definition it is a closed subset A of [a,b]. Moreover μ((1-χA)f) =0, so that μ(f) = 0 if f vanishes on A.
Spectral measure
Let H be a Hilbert space and T a self-adjoint bounded operatorBounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
on H with 0 ≤ T ≤ I, so that the spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
σ(T) of T is contained in [0,1]. If p(t) is a complex polynomial, then by the spectral mapping theorem
- σ(p(T)) = p(σ(T))
and hence
- ||p(T)|| ≤ ||p||∞,
where ||·||∞ denotes the uniform norm on C[0,1]. By the Weierstrass approximation theorem, polynomials are uniformly dense in C[0, 1]. It follows that f(T) can be defined for every f in C[0,1], with
- σ(f(T)) = f(σ(T)) and ||f(T)|| ≤ ||f||∞.
If 0 ≤ g ≤ 1 is a lower semicontinuous function on [0,1], for example the characteristic function χ[0,α] of a subinterval of [0,1], then
g is a pointwise increasing limit of non-negative fn in C[0,1].
According to Sz.-Nagy
Bela Szokefalvi-Nagy
Béla Szőkefalvi-Nagy was a Hungarian mathematician. His father, Gyula Szőkefalvi-Nagy was also a famed mathematician. Szőkefalvi-Nagy collaborated with Alfréd Haar and Frigyes Riesz, founders of the Szegedian school of mathematics. He contributed to the theory of Fourier series and approximation...
, if ξ is a vector in H, then the vectors
- ηn = fn(T) ξ
form a Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
in H, since, for n ≥ m,
and (ηn,ξ) = (fn(T)ξ, ξ) is bounded and increasing, so has a limit.
It follows that g(T) can be defined by
- g(T)ξ = lim fn(T)ξ.
If ξ and η are vectors in H, then
defines a bounded linear form μξ,η on H. By the Riesz representation theorem
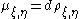
for a unique normalised function ρξ,η of bounded variation on [0,1].
dρξ,η (or sometimes slightly incorrectly ρξ,η itself) is called the spectral measure
determined by ξ and η.
The operator g(T) is accordingly uniquely characterised by the equation
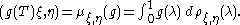
The spectral projection
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
E(λ) is defined by
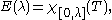
so that
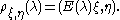
It follows that
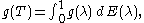
which is understood in the sense that for any vectors ξ and η,
For a single vector ξ, μξ = μξ,ξ is a positive form on [0,1]
(in other words proportional to a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
on [0,1]) and ρξ = ρξ,ξ is non-negative and non-decreasing.
Polarisation shows that all the forms μξ,η can naturally be expressed in terms of such positive forms, since
- μξ,η = ¼(μξ+η + i μξ+iη − μξ−η −i μξ−iη).
If the vector ξ is such that the linear span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
of the vectors (Tnξ) is dense in H, i.e. ξ is a cyclic vector for
T, then the map U defined by
satisfies
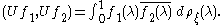
Let L2([0,1], dρξ) denote the Hilbert space completion of C[0,1] associated
with the possibly degenerate inner product on the right hand side.
Thus U extends to a unitary transformation
Unitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
of L2([0,1], dρξ) onto H. UTU* is then just multiplication by λ on L2([0,1], dρξ); and more generally Uf(T)U* is multiplication by f(λ). In this case, the support of dρξ
is exactly σ(T), so that
- the self-adjoint operator becomes a multiplication operator on the space of functions on its spectrum with inner product given by the spectral measure.
Weyl–Kodaira theory
The eigenfunction expansion associated with singular differential operators of the formon an open interval (a, b) requires an initial analysis of the behaviour of the fundamental
eigenfunctions near the endpoints a and b to determine possible boundary conditions there.
Unlike the regular Sturm–Liouville case, in some circumstances spectral values
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
of D can have multiplicity
2. In the development outlined below standard assumptions will be imposed on p and q that guarantee that the spectrum of
D has multiplicity one everywhere and is bounded below.
This includes almost all important applications; modifications required for the more general case will be discussed later.
Having chosen the boundary conditions, as in the classical theory the resolvent of D, (D + R )−1 for R large and positive, is
given by an operator T corresponding to a Green's function constructed from two fundamental eigenfunctions.
In the classical case T was a compact self-adjoint operator; in this case T is just a self-adjoint bounded operator with 0 ≤ T ≤ I.
The abstract theory of spectral measure can therefore be applied to T to give the eigenfunction expansion for D.
The central idea in the proof of Weyl and Kodaira can be explained informally as follows. Assume that the spectrum of D lies in [1,∞) and that T =D−1 and let
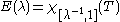
be the spectral projection of D corresponding to the interval [1,λ]. For an arbitrary function f define
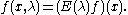
f(x,λ) may be regarded as a differentiable map into the space of functions of bounded variation ρ; or equivalently as a differentiable map
into the Banach space E of bounded linear functionals dρ on C[α,β] whenever [α,β] is a compact subinterval of [1, ∞).
Weyl's fundamental observation was that dλ f satisfies a second order ordinary differential equation taking values in E:
After imposing initial conditions on the first two derivatives at a fixed point c, this equation can be solved explicitly
in terms of the two fundamental eigenfunctions and the "initial value" functionals
This point of view may now be turned on its head: f(c,λ) and fx(c,λ) may be written as
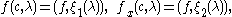
where ξ1(λ) and ξ2(λ) are given purely in terms of the fundamental eigenfunctions.
The functions of bounded variation
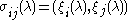
determine a spectral measure on the spectrum of D and can be computed explicitly from the behaviour
of the fundamental eigenfunctions (the Titchmarsh–Kodaira formula).
Limit circle and limit point for singular equations
Let q(x) be a continuous real-valued function on (0,∞)and let D be the second order differential operator
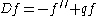
on (0,∞). Fix a point c in (0,∞) and, for λ complex, let φλ, χλ be the unique fundamental eigenfunctions of D on (0,∞) satisfying
together with the initial conditions at c
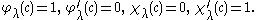
Then their Wronskian satisfies
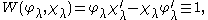
since it is constant and equal to 1 at c.
If λ is non-real and 0 < x < ∞, then Green's formula implies
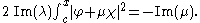
This defines a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
in the complex μ-plane, the interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of which is given by
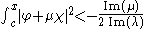
if x > c and by
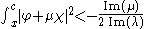
if x < c.
Let Dx be the closed disc enclosed by the circle. By definition
these closed discs are nested and decrease as x approaches 0 or ∞. So in the limit, the circles
tend either to a limit circle or a limit point at each end. In particular if μ is a
limit point or a point on the limit circle at 0 or ∞, then |φ + μχ|2 is
square integrable (L2) near 0 or ∞. In particular:
- there are always non-zero solutions of Df = λf which are square integrable near 0 or ∞;
- there is exactly one non-zero solution (up to scalar multiples) of Df = λf which is square integrable near 0 or ∞ precisely in the limit point case.
On the other hand if Dg = λ' g for another value λ', then
satisfies Dh = λh, so that
Using this to estimate g, it follows that
- the limit point/limit circle behaviour at 0 or ∞ is independent of the choice of λ.
More generally if Dg= (λ – r) g for some function r(x), then
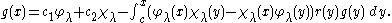
From this it follows that
- if r is continuous at 0, then D + r is limit point or limit circle at 0 precisely when D is,
so that in particular
- if q(x)- a/x2 is continuous at 0, then D is limit point at 0 if and only if a ≥ ¾.
Similarly
- if r has a finite limit at ∞, then D + r is limit point or limit circle at ∞ precisely when D is,
so that in particular
- if q has a finite limit at ∞, then D is limit point at ∞.
Many more elaborate criteria to be limit point or limit circle can be found in the mathematical literature.
Green's function (singular case)
Consider the differential operatoron (0,∞) with q0 positive and continuous on (0,∞) and p0 continuously differentiable in [0,∞), positive in (0,∞) and p0(0)=0.
Moreover assume that after reduction to standard form
D0 becomes the equivalent operator
on (0,∞) where q has a finite limit at ∞. Thus
- D is limit point at ∞.
At 0, D may be either limit circle or limit point. In either case there is an eigenfunction Φ0 with DΦ0=0 and Φ0 square integrable near 0. In the limit circle case, Φ0 determines a boundary condition at 0:
For λ complex, let Φλ and Χλ satisfy
- (D – λ)Φλ = 0, (D – λ)Χλ = 0
- Χλ square integrable near infinity
- Φλ square integrable at 0 if 0 is limit point
- Φλ satisfies the boundary condition above if 0 is limit circle.
Let
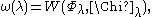
a constant which vanishes precisely when Φλ and Χλ are proportional, i.e. λ is an eigenvalue of D for these boundary conditions.
On the other hand, this cannot occur if Im λ ≠ 0 or if λ is negative.
Indeed if D f= λf with q0 – λ ≥ δ >0, then by Green's formula (Df,f) = (f,Df), since W(f,f*) is constant. So λ must be real. If f is taken to be real-valued in the D0 realization, then for 0 < x < y
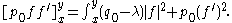
Since p0(0) = 0 and f is integrable near 0, p0f f ' must vanish at 0. Setting x = 0, it follows that f(y) f '(y) >0, so that f2 is increasing, contradicting the square integrability of f near ∞.
Thus, adding a positive scalar to q, it may be assumed that
- ω(λ) ≠ 0 when λ is not in [1,∞).
If ω(λ) ≠ 0, the Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
Gλ(x,y) at λ is defined by
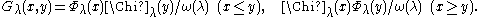
and is independent of the choice of λ and Χλ.
In the examples there will be a third "bad" eigenfunction Ψλ defined and holomorphic for λ not in [1, ∞) such that
Ψλ satisfies the boundary conditions at neither 0 nor ∞. This means that for λ not in [1, ∞)
- W(Φλ,Ψλ) is nowhere vanishing;
- W(Χλ,Ψλ) is nowhere vanishing.
In this case Χλ is proportional to Φλ + m(λ) Ψλ, where
- m(λ) = – W(Φλ,Χλ) / W(Ψλ,Χλ).
Let H1 be the space of square integrable continuous functions on (0,∞) and let H0 be
- the space of C2 functions f on (0,∞) of compact support if D is limit point at 0
- the space of C2 functions f on (0,∞) with W(f,Φ0)=0 at 0 and with f = 0 near ∞ if D is limit circle at 0.
Define T = G0 by
Then T D = I on H0, D T = I on H1 and the operator D is bounded below on H0:
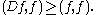
Thus T is a self-adjoint bounded operator with 0 ≤ T ≤ I.
Formally T = D−1. The corresponding operators Gλ defined for λ not in [1,∞) can be formally identified with
and satisfy Gλ (D – λ) = I on H0, (D – λ)Gλ = I on H1.
Spectral theorem and Titchmarsh–Kodaira formula
Theorem. For every real number λ let ρ(λ) be defined by the Titchmarsh–Kodaira formula:ψψ
Then ρ(λ) is a lower semicontinuous non-decreasing function of λ and if
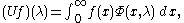
then U defines a unitary transformation of L2(0,∞) onto L2([1,∞), dρ) such that
UDU−1 corresponds to multiplication by λ.
The inverse transformation U−1 is given by
The spectrum of D equals the support of dρ.
Kodaira gave a streamlined version of Weyl's original proof. (M.H. Stone
Marshall Harvey Stone
Marshall Harvey Stone was an American mathematician who contributed to real analysis, functional analysis, and the study of Boolean algebras.-Biography:...
had previously shown how part of Weyl's work could be simplified using von Neumann's spectral theorem.)
In fact for T =D−1 with 0 ≤ T ≤ I, the spectral projection E(λ) of T is defined by
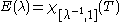
It is also the spectral projection of D corresponding to the interval [1,λ].
For f in H1 define
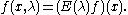
f(x,λ) may be regarded as a differentiable map into the space of functions ρ of bounded variation; or equivalently as a differentiable map
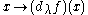
into the Banach space E of bounded linear functionals dρ on C[α,β] for any compact subinterval [α,β] of [1, ∞).
The functionals (or measures) dλ f(x) satisfies the following E-valued second order ordinary differential equation:
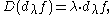
with initial conditions at c in (0,∞)
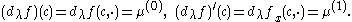
If φλ and χλ are the special eigenfunctions adapted to c, then
Moreover
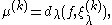
where
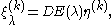
with
(As the notation suggests, ξλ(0) and ξλ(1) do not depend on the choice of z.)
Setting
it follows that
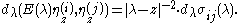
On the other hand there are holomorphic functions
a(λ), b(λ) such that
- φλ + a(λ) χλ is proportional to Φλ;
- φλ + b(λ) χλ is proportional to Χλ.
Since W(φλ,χλ) = 1, the Green's function is given by
Direct calculation shows that
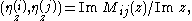
where the so-called characteristic matrix Mij(z) is given by
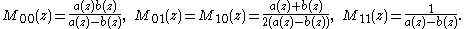
Hence
which immediately implies
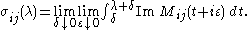
(This is a special case of the "Stietljes inversion formula".)
Setting ψλ(0)=φλ and ψλ(1)=χλ, it follows that
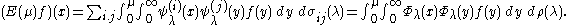
This identity is equivalent to the spectral theorem and Titchmarsh–Kodaira formula.
Application to the hypergeometric equation
The Mehler–Fock transform concerns the eigenfunction expansion associated with the Legendre differential operatorLegendre function
In mathematics, the Legendre functions Pλ, Qλ and associated Legendre functions P, Q are generalizations of Legendre polynomials to non-integer degree.-Differential equation:...
D
on (1,∞). The eigenfunctions are the Legendre function
Legendre function
In mathematics, the Legendre functions Pλ, Qλ and associated Legendre functions P, Q are generalizations of Legendre polynomials to non-integer degree.-Differential equation:...
s
with eigenvalue λ ≥ 0. The two Mehler–Fock transformations are
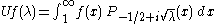
and
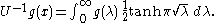
(Often this is written in terms of the variable τ = √λ.)
Mehler and Fock studied this differential operator because it arose as the radial component of the Laplacian on 2-dimensional hyperbolic space.
More generally, consider the group G = SU(1,1) consisting of complex matrices of the form
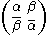
with determinant |α|2 − |β|2 = 1.