
Wronskian
Encyclopedia
In mathematics
, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent
.
More generally, for n real
- or complex
-valued functions f1, ..., fn, which are n − 1 times differentiable on an interval
I, the Wronskian W(f1, ..., fn) as a function on I is defined by
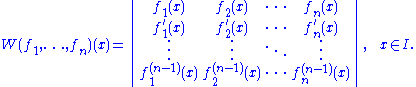
That is, it is the determinant
of the matrix constructed by placing the functions in the first row, the first derivative of each function in the second row, and so on through the (n - 1)st derivative, thus forming a square matrix sometimes called a fundamental matrix.
When the functions fi are solutions of a linear differential equation
, the Wronskian can be found explicitly using Abel's identity
, even if the functions fi are not known explicitly.
on an interval by showing that it does not vanish identically.
A common misconception is that W = 0 everywhere implies linear dependence, but pointed out that the functions x2 and |x|x have continuous derivatives and their Wronskian vanishes everywhere, yet they are not linearly dependent in a neighborhood of 0. There are several extra conditions which ensure that the vanishing of the Wronskian in an interval implies linear dependence.
observed that if the functions are analytic, then the vanishing of the Wronskian in an interval implies that they are linearly dependent. gave several other conditions for the vanishing of the Wronskian to imply linear dependence; for example, if the Wronskian of n functions is identically zero and the n Wronskians of n–1 of them do not all vanish at any point then the functions are linearly dependent. gave a more general condition that together with the vanishing of the Wronskian implies linear dependence.
. For more general conditions under which the converse is valid see .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
.
Definition
The Wronskian of two functions f and g is W(f,g) = fg′–gf ′.More generally, for n real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
- or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued functions f1, ..., fn, which are n − 1 times differentiable on an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
I, the Wronskian W(f1, ..., fn) as a function on I is defined by
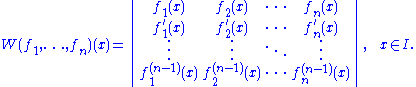
That is, it is the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the matrix constructed by placing the functions in the first row, the first derivative of each function in the second row, and so on through the (n - 1)st derivative, thus forming a square matrix sometimes called a fundamental matrix.
When the functions fi are solutions of a linear differential equation
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
, the Wronskian can be found explicitly using Abel's identity
Abel's identity
In mathematics, Abel's identity is an equation that expresses the Wronskian of two homogeneous solutions of a second-order linear ordinary differential equation in terms of a coefficient of the original differential equation.The relation can be generalised to nth-order linear ordinary differential...
, even if the functions fi are not known explicitly.
The Wronskian and linear independence
If the functions fi are linearly dependent, then so are the columns of the Wronskian as differentiation is a linear operation, so the Wronskian vanishes. So the Wronskian can be used to show that a set of differentiable functions is linearly independentLinear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
on an interval by showing that it does not vanish identically.
A common misconception is that W = 0 everywhere implies linear dependence, but pointed out that the functions x2 and |x|x have continuous derivatives and their Wronskian vanishes everywhere, yet they are not linearly dependent in a neighborhood of 0. There are several extra conditions which ensure that the vanishing of the Wronskian in an interval implies linear dependence.
observed that if the functions are analytic, then the vanishing of the Wronskian in an interval implies that they are linearly dependent. gave several other conditions for the vanishing of the Wronskian to imply linear dependence; for example, if the Wronskian of n functions is identically zero and the n Wronskians of n–1 of them do not all vanish at any point then the functions are linearly dependent. gave a more general condition that together with the vanishing of the Wronskian implies linear dependence.
Generalized Wronskians
For n functions of several variables, a generalized Wronskian is the determinant of an n by n matrix with entries Di(fj) (with 0≤i<n), where each Di is some constant coefficient linear partial differential operator of order i. If the functions are linearly dependent then all generalized Wronskians vanish. As in the 1 variable case the converse is not true in general: if all generalized Wronskians vanish this does not imply that the functions are linearly dependent. However the converse is true in many special cases. For example, if the functions are polynomials and all generalized Wronskians vanish, then the functions are linearly dependent. Roth used this result about generalized Wronskians in his proof of Roth's theoremThue–Siegel–Roth theorem
In mathematics, the Thue–Siegel–Roth theorem, also known simply as Roth's theorem, is a foundational result in diophantine approximation to algebraic numbers. It is of a qualitative type, stating that a given algebraic number α may not have too many rational number approximations, that are 'very...
. For more general conditions under which the converse is valid see .
See also
- Moore matrix, analogous to the Wronskian with differentiation replaced by the Frobenius endomorphismFrobenius endomorphismIn commutative algebra and field theory, the Frobenius endomorphism is a special endomorphism of commutative rings with prime characteristic p, an important class which includes finite fields. The endomorphism maps every element to its pth power...
over a finite field.

