Frobenius endomorphism
Encyclopedia
In commutative algebra
and field theory
, the Frobenius endomorphism (after Ferdinand Georg Frobenius
) is a special endomorphism
of commutative rings
with prime characteristic
p, an important class which includes finite fields
. The endomorphism maps every element to its pth power. In certain contexts it is an automorphism
, but this is not true in general.
for all r in R. Clearly this respects the multiplication of R:
and F(1) is clearly 1 also. What is interesting, however, is that it also respects the addition of R. The expression (r + s)p can be expanded using the binomial theorem
. Because p is prime, it divides p! but not any q! for q < p; it therefore will divide the numerator, but not the denominator, of the explicit formula of the binomial coefficient
s
for 1 ≤ k ≤ p − 1. Therefore the coefficients of all the terms except rp and sp are divisible by p, the characteristic, and hence they vanish. Thus
This shows that F is a ring homomorphism.
In general, F is not an automorphism. For example, let K be the field Fp(t), that is, the finite field with p elements together with a single transcendental element. We claim that the image of F does not contain t. We will prove this by contradiction: Suppose that there is an element of K whose image under F is t. This element is a rational function q(t)/r(t) whose p' th power (q(t)/r(t))p equals t. This makes p(deg q - deg r) = 1, which is impossible. So F is not surjective and hence not an automorphism. It is also possible for F to be non-injective. This occurs if and only if R has a nilpotent
element ≠0. (An example is Fp[T]/T2, where F(T)=0, but T≠0.)
Iterating the Frobenius map gives us a sequence of elements in R:
Applying the e' th iterate of F to a ring which contains a field K of pe elements gives us a fixed point set equal to K, similar to the example above. The iterates of the Frobenius map are also used in defining the Frobenius closure and tight closure
of an ideal.
of any extension of finite fields.
However, F is not necessarily an endomorphism of k-schemes. If k is not
, then F will not fix k, and consequently F will not be a k-algebra map. A partial resolution of this problem is to endow X with a different structure of k-scheme: consider the ring map 
given by 
, denote by X the corresponding k-scheme. Then F induces a morphism of k-schemes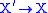 
.
This solution is not very satisfactory. For example, if X is of finite type over k, then X is not (if k is not of finite type over its prime field). Even over a function field k over a finite field, the smoothness is lost. To preserve the properties of the k-scheme X, one then introduces the relative Frobenius
which is obtained by base change of X by 
.
The definition of the Frobenius for finite fields can be extended to other sorts of field extensions. Given an unramified finite extension L/K of local field
s, there is a concept of Frobenius endomorphism which induces the Frobenius endomorphism in the corresponding extension of residue field
s.
Suppose L/K is an unramified extension of local fields, with ring of integers
OK of K such that the residue field, the integers of K modulo their unique maximal ideal φ, is a finite field of order q. If Φ is a prime of L lying over φ, that L/K is unramified means by definition that the integers of L modulo Φ, the residue field of L, will be a finite field of order qf extending the residue field of K where f is the degree of L/K. We may define the Frobenius map for elements of the ring of integers OL of L as an automorphism
of L such that
, Frobenius elements are defined for extensions L/K of global field
s that are finite Galois extension
s for prime ideal
s Φ of L that are unramified in L/K. Since the extension is unramified the decomposition group of Φ is the Galois group of the extension of residue fields. The Frobenius element then can be defined for elements of the ring of integers of L as in the local case, by
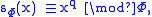
where q is the order of the residue field OK mod Φ.
Lifts of the frobenius are in correspondence with p-derivations.
has discriminant
and so is unramified at the prime 3; it is also irreducible mod 3. Hence adjoining a root ρ of it to the field of 3-adic numbers
gives an unramified extension 
of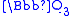 
. We may find the image of ρ under the Frobenius map by locating the root nearest to ρ3, which we may do by Newton's method
. We obtain an element of the ring of integers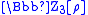
in this way; this is a polynomial of degree four in ρ with coefficients in the 3-adic integers 
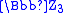. Modulo 38 this polynomial is
.
This is algebraic over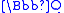
and is the correct global Frobenius image in terms of the embedding of 
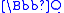into 
; moreover, the coefficients are algebraic and the result can be expressed algebraically. However, they are of degree 120, the order of the Galois group, illustrating the fact that explicit computations are much more easily accomplished if p-adic results will suffice.
If L/K is an abelian extension of global fields, we get a much stronger congruence since it depends only on the prime φ in the base field K. For an example, consider the extension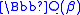
of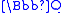 
obtained by adjoining a root β satisfying
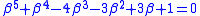
to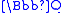
. This extension is cyclic of order five, with roots
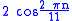
for integer n. It has roots which are Chebyshev polynomials
of β:
give the result of the Frobenius map for the primes 2, 3 and 5, and so on for larger primes not equal to 11 or of the form 22n+1 (which split). It is immediately apparent how the Frobenius map gives a result equal mod p to the p-th power of the root β.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
and field theory
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
, the Frobenius endomorphism (after Ferdinand Georg Frobenius
Ferdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
) is a special endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
of commutative rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
with prime characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
p, an important class which includes finite fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. The endomorphism maps every element to its pth power. In certain contexts it is an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
, but this is not true in general.
Definition
Let R be a commutative ring with prime characteristic p (an integral domain of positive characteristic always has prime characteristic, for example). The Frobenius endomorphism F is defined by- F(r) = rp
for all r in R. Clearly this respects the multiplication of R:
- F(rs) = (rs)p = rpsp = F(r)F(s),
and F(1) is clearly 1 also. What is interesting, however, is that it also respects the addition of R. The expression (r + s)p can be expanded using the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
. Because p is prime, it divides p! but not any q! for q < p; it therefore will divide the numerator, but not the denominator, of the explicit formula of the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s
for 1 ≤ k ≤ p − 1. Therefore the coefficients of all the terms except rp and sp are divisible by p, the characteristic, and hence they vanish. Thus
- F(r + s) = (r + s)p = rp + sp = F(r) + F(s).
This shows that F is a ring homomorphism.
In general, F is not an automorphism. For example, let K be the field Fp(t), that is, the finite field with p elements together with a single transcendental element. We claim that the image of F does not contain t. We will prove this by contradiction: Suppose that there is an element of K whose image under F is t. This element is a rational function q(t)/r(t) whose p
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
element ≠0. (An example is Fp[T]/T2, where F(T)=0, but T≠0.)
Fixed points of the Frobenius endomorphism
Say R is an integral domain. The Frobenius map fixes all the elements of R which satisfy the equation xp = x. These are all the roots of the equation xp - x, and since this equation has degree p, there are at most p roots. These are exactly the elements 0, 1, 2, ..., p - 1, so the fixed point set of F is the prime field.Iterating the Frobenius map gives us a sequence of elements in R:
Applying the e
Tight closure
In mathematics, in the area of commutative algebra, tight closure is an operation defined on ideals in positive characteristic. It was introduced by Mel Hochster and Craig Huneke in the 1980s....
of an ideal.
Frobenius for finite fields
Let Fq be the finite field of q elements, where q=pe. F fixes Fp by the argument above. If e=2, then F2, the second iterate of Frobenius, fixes p2 elements, so it will fix Fp2. In general, Fe fixes Fpe. Furthermore, F will generate the Galois groupGalois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of any extension of finite fields.
Frobenius for schemes
Using the setup above, it is easy to extend the Frobenius map to the context of schemes. Let X be a scheme over a field k of characteristic p. Choose an open affine subset U=Spec R. Since X is a k-scheme, we get an inclusion of k in R. This forces R to be a characteristic p ring, so we can define the Frobenius endomorphism F for R as we did above. It is clear that F commutes with localization, so F glues to give an endomorphism of X, called the absolute Frobenius map.However, F is not necessarily an endomorphism of k-schemes. If k is not
, then F will not fix k, and consequently F will not be a k-algebra map. A partial resolution of this problem is to endow X with a different structure of k-scheme: consider the ring map given by , denote by X the corresponding k-scheme. Then F induces a morphism of k-schemes 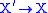.This solution is not very satisfactory. For example, if X is of finite type over k, then X is not (if k is not of finite type over its prime field). Even over a function field k over a finite field, the smoothness is lost. To preserve the properties of the k-scheme X, one then introduces the relative Frobenius
which is obtained by base change of X by .Frobenius for local fields
The definition of F for schemes automatically defines F for local and global fields, but we will treat these cases separately for clarity.The definition of the Frobenius for finite fields can be extended to other sorts of field extensions. Given an unramified finite extension L/K of local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
s, there is a concept of Frobenius endomorphism which induces the Frobenius endomorphism in the corresponding extension of residue field
Residue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
s.
Suppose L/K is an unramified extension of local fields, with ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
OK of K such that the residue field, the integers of K modulo their unique maximal ideal φ, is a finite field of order q. If Φ is a prime of L lying over φ, that L/K is unramified means by definition that the integers of L modulo Φ, the residue field of L, will be a finite field of order qf extending the residue field of K where f is the degree of L/K. We may define the Frobenius map for elements of the ring of integers OL of L as an automorphism
of L such thatFrobenius for global fields
In algebraic number theoryAlgebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, Frobenius elements are defined for extensions L/K of global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s that are finite Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
s for prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s Φ of L that are unramified in L/K. Since the extension is unramified the decomposition group of Φ is the Galois group of the extension of residue fields. The Frobenius element then can be defined for elements of the ring of integers of L as in the local case, by
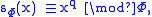
where q is the order of the residue field OK mod Φ.
Lifts of the frobenius are in correspondence with p-derivations.
Examples
The polynomial- x5 − x − 1
has discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
- 19 × 151,
and so is unramified at the prime 3; it is also irreducible mod 3. Hence adjoining a root ρ of it to the field of 3-adic numbers
gives an unramified extension of 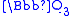. We may find the image of ρ under the Frobenius map by locating the root nearest to ρ3, which we may do by Newton's methodNewton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
. We obtain an element of the ring of integers
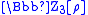in this way; this is a polynomial of degree four in ρ with coefficients in the 3-adic integers 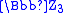. Modulo 38 this polynomial is.This is algebraic over
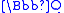and is the correct global Frobenius image in terms of the embedding of 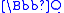into ; moreover, the coefficients are algebraic and the result can be expressed algebraically. However, they are of degree 120, the order of the Galois group, illustrating the fact that explicit computations are much more easily accomplished if p-adic results will suffice.If L/K is an abelian extension of global fields, we get a much stronger congruence since it depends only on the prime φ in the base field K. For an example, consider the extension
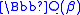of 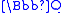obtained by adjoining a root β satisfying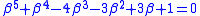to
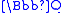. This extension is cyclic of order five, with roots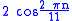for integer n. It has roots which are Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
of β:
- β2 - 2, β3 - 3β, β5-5β3+5β
give the result of the Frobenius map for the primes 2, 3 and 5, and so on for larger primes not equal to 11 or of the form 22n+1 (which split). It is immediately apparent how the Frobenius map gives a result equal mod p to the p-th power of the root β.