Residue field
Encyclopedia
In mathematics
, the residue field is a basic construction in commutative algebra
. If R is a commutative ring
and m is a maximal ideal
, then the residue field is the quotient ring
k = R/m, which is a field
. Frequently, R is a local ring
and m is then its unique maximal ideal.
This construction is applied in algebraic geometry
, where to every point x of a scheme
X one associates its residue field k(x). One can say a little loosely that the residue field of a point of an abstract algebraic variety
is the 'natural domain' for the coordinates of the point.
, with the maximal ideal m. Then the residue field is the quotient ring R/m.
Now suppose that X is a scheme
and x is a point of X. By the definition of scheme, we may find an affine neighbourhood U = Spec A, with A some commutative ring
. Considered in the neighbourhood U, the point x corresponds to a prime ideal
p ⊂ A (see Zariski topology
). The local ring
of X in x is by definition the localization
R = Ap, with the maximal ideal m = p·Ap. Applying the construction above, we obtain the residue field of the point x :
One can prove that this definition does not depend on the choice of the affine neighbourhood U.
A point is called K-rational
for a certain field K, if k(x) ⊂ K.
k. If k is algebraically closed
, there are exactly two types of prime ideals, namely
The residue fields are
If k is not algebraically closed, then more types arise, for example if k = R, then the prime ideal (x2 + 1) has residue field isomorphic to C.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the residue field is a basic construction in commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
. If R is a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
and m is a maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
, then the residue field is the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
k = R/m, which is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. Frequently, R is a local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
and m is then its unique maximal ideal.
This construction is applied in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, where to every point x of a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
X one associates its residue field k(x). One can say a little loosely that the residue field of a point of an abstract algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
is the 'natural domain' for the coordinates of the point.
Definition
Suppose that R is a commutative local ringLocal ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
, with the maximal ideal m. Then the residue field is the quotient ring R/m.
Now suppose that X is a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
and x is a point of X. By the definition of scheme, we may find an affine neighbourhood U = Spec A, with A some commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. Considered in the neighbourhood U, the point x corresponds to a prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
p ⊂ A (see Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
). The local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
of X in x is by definition the localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
R = Ap, with the maximal ideal m = p·Ap. Applying the construction above, we obtain the residue field of the point x :
- k(x) := Ap / p·Ap.
One can prove that this definition does not depend on the choice of the affine neighbourhood U.
A point is called K-rational
Rational point
In number theory, a K-rational point is a point on an algebraic variety where each coordinate of the point belongs to the field K. This means that, if the variety is given by a set of equationsthen the K-rational points are solutions ∈Kn of the equations...
for a certain field K, if k(x) ⊂ K.
Example
Consider the affine line A1k = Spec k[t] over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k. If k is algebraically closed
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
, there are exactly two types of prime ideals, namely
- (t − a), a ∈ k
- (0), the zero-ideal.
The residue fields are
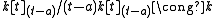
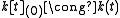, the function field over k in one variable.
If k is not algebraically closed, then more types arise, for example if k = R, then the prime ideal (x2 + 1) has residue field isomorphic to C.
Properties
- For a scheme locally of finite type over a field k, a point x is closed if and only if k(x) is a finite extension of the base field k. This is a geometric formulation of Hilbert's NullstellensatzHilbert's NullstellensatzHilbert's Nullstellensatz is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of mathematics. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields...
. In the above example, the points of the first kind are closed, having residue field k, whereas the second point is the generic pointGeneric pointIn mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
, having transcendence degreeTranscendence degreeIn abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
1 over k. - A morphism Spec K → X, K some field, is equivalent to giving a point x ∈ X and an extensionField extensionIn abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
K/k(x). - The dimensionKrull dimensionIn commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
of a scheme of finite type over a field is equal to the transcendence degree of the residue field of the generic point.