Bounded variation
Encyclopedia
In mathematical analysis
, a function of bounded variation, also known as a BV function, is a real
-valued function
whose total variation
is bounded (finite): the graph of a function
having this property is well behaved in a precise sense. For a continuous function
of a single variable
, being of bounded variation means that the distance
along the direction
of the y-axis, neglecting the contribution of motion along x-axis, traveled by a point moving along the graph has a finite value. For a continuous function of several variables, the meaning of the definition is the same, except for the fact that the continuous path to be considered cannot be the whole graph of the given function (which is an hypersurface in this case), but can be every intersection
of the graph itself with a hyperplane
(in the case of functions of two variables, a plane
) parallel to a fixed x-axis and to the y-axis.
Functions of bounded variation are precisely those with respect to which one may find Riemann–Stieltjes integrals of all continuous functions.
Another characterization states that the functions of bounded variation on a closed interval are exactly those f which can be written as a difference g − h, where both g and h are bounded monotone
.
In the case of several variables, a function f defined on an open subset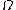
of ℝn is said to have bounded variation if its distributional derivative
is a finite vector
Radon measure
.
One of the most important aspects of functions of bounded variation is that they form an algebra
of discontinuous functions
whose first derivative exists almost everywhere
: due to this fact, they can and frequently are used to define generalized solutions of nonlinear problems involving functional
s, ordinary
and partial differential equation
s in mathematics
, physics
and engineering
. Considering the problem of multiplication of distributions or more generally the problem of defining general nonlinear operations on generalized function
s, function of bounded variation are the smallest algebra
which has to be embedded in every space of generalized function
s preserving the result of multiplication
.
, in the paper dealing with the convergence of Fourier series
. The first successful step in the generalization of this concept to functions of several variables was due to Leonida Tonelli
, who introduced a class of continuous
BV functions in 1926 , to extend his direct method for finding solutions to problems in the calculus of variations
in more than one variable. Ten years after, in , Lamberto Cesari
changed the continuity
requirement in Tonelli's definition to a less restrictive integrability
requirement, obtaining for the first time the class of functions of bounded variation of several variables in its full generality: as Jordan did before him, he applied the concept to resolve of a problem concerning the convergence of Fourier series
, but for functions of two variables. After him, several authors applied BV functions to study Fourier series
in several variables, geometric measure theory
, calculus of variations
, and mathematical physics
. Renato Caccioppoli
and Ennio de Giorgi
used them to define measure of non smooth
boundaries
of sets (see the entry "Caccioppoli set
" for further informations). Olga Arsenievna Oleinik
introduced her view of generalized solutions for nonlinear partial differential equation
s as functions from the space BV in the paper , and was able to construct a generalized solution of bounded variation of a first order partial differential equation in the paper : few years later, Edward D. Conway and Joel A. Smoller applied BV-functions to the study of a single nonlinear hyperbolic partial differential equation of first order in the paper , proving that the solution of the Cauchy problem
for such equations is a function of bounded variation, provided the initial value
belongs to the same class. Aizik Isaakovich Vol'pert
developed extensively a calculus for BV functions: in the paper he proved the chain rule for BV functions and in the book he, jointly with his pupil Sergei Ivanovich Hudjaev, explored extensively the properties of BV functions and their application. His chain rule formula was later extended by Luigi Ambrosio
and Gianni Dal Maso in the paper .
-valued (or more generally complex
-valued) function
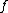, defined on an interval
[a , b]⊂ℝ is the quantity
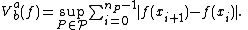
where the supremum
is taken over the set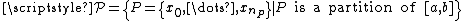
of all partitions
of the interval considered.
If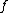
is differentiable
and its derivative is Riemann-integrable, its total variation is the vertical component of the arc-length
of its graph, that is to say,
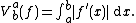
A real-valued function
on the real line
is said to be of bounded variation (BV function) on a chosen interval
⊂ℝ if its total variation is finite, i.e.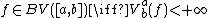
It can be proved that a real function ƒ is of bounded variation in an interval if and only if it can be written as the difference ƒ = ƒ1 − ƒ2 of two non-decreasing functions: this result is known as the Jordan decomposition
.
Through the Stieltjes integral, any function of bounded variation on a closed interval [a, b] defines a bounded linear functional on C([a, b]). In this special case, the Riesz representation theorem
states that every bounded linear functional arises uniquely in this way. The normalised positive functionals or probability measure
s correspond to positive non-decreasing lower semicontinuous functions. This point of view has been important in
spectral theory
, in particular in its application to ordinary differential equations
.
, are functions whose distributional derivative
is a finite Radon measure
. More precisely:
Let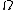
be an open subset of ℝn. A function 
belonging to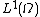 
is said of bounded variation (BV function), and write
if there exists a finite vector Radon measure
such that the following equality holds
that is,
defines a linear functional
on the space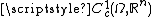
of continuously differentiable
vector functions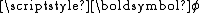
of compact support contained in 
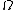: the vector measure
represents therefore the distributional or weak
gradient
of
.
An equivalent definition is the following.
Given a function
belonging to 
, the total variation of 
in is defined as
where
is the essential supremum norm
. Sometimes, especially in the theory of Caccioppoli set
s, the following notation is used
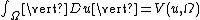
in order to emphasize that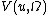
is the total variation of the distributional / weak
gradient
of
. This notation reminds also that if 
is of class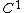 
(i.e. a continuous
and differentiable function
having continuous
derivative
s) then its variation
is exactly the integral of the absolute value
of its gradient
.
The space of functions of bounded variation (BV functions) can then be defined as
The two definitions are equivalent since if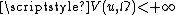
then
therefore
defines a continuous linear functional on
the space
. Since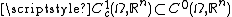 
as a linear subspace
, this continuous linear functional can be extended continuously
and linearily to the whole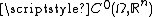
by the Hahn–Banach theorem
i.e. it defines a Radon measure.
of locally integrable function
s, i.e. function
s belonging to
, is considered in the preceding definitions , and instead of the one of globally integrable functions, then the function space defined is that of functions of locally bounded variation. Precisely, developing this idea for , a local
variation is defined as follows,
for every set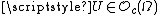
, having defined 
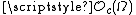as the set of all precompact
open subsets of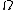
with respect to the standard topology
of finite dimensional vector space
s, and correspondingly the class of functions of locally bounded variation is defined as
The second one, which is adopted in references and (partially), is the following:
s of one variable and to function
s of several variables will be considered in the following, and proof
s will be carried on only for functions of several variables since the proof
for the case of one variable is a straightforward adaptation of the several variables case: also, in each section it will be stated if the property is shared also by functions of locally bounded variation or not. References , and are extensively used.
in the interval
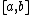⊂ℝ of definition of the function 
, either one of the following two assertions is true
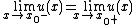
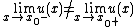
while both limits
exist and are finite. In the case of functions of several variables, there are some premises to understand: first of all, there is a continuum
of direction
s along which it is possible to approach a given point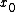
belonging to the domain 
⊂ℝn. It is necessary to make precise a suitable concept of limit
: choosing a unit vector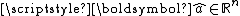
it is possible to divide 
in two sets
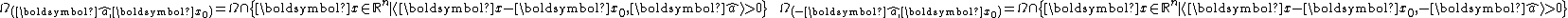
Then for each point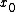
belonging to the domain 
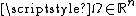of the BV function 
, only one of the following two assertions is true
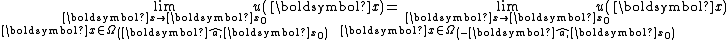
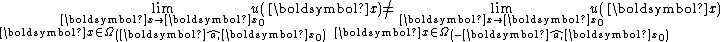
or
belongs to a subset
of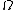
having zero 
-dimensional Hausdorff measure
. The quantities
are called approximate limits of the BV function
at the point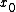 
.
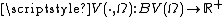is lower semi-continuous
:
to see this, choose a Cauchy sequence
of BV-functions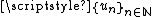
converging to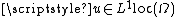 
. Then, since all the functions of the sequence and their limit function are integrable
and by the definition of lower limit
Now considering the supremum
on the set of functions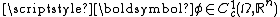
such that 
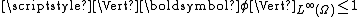then the following inequality holds true
which is exactly the definition of lower semicontinuity.
is a subset
of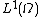
, while linearity follows from the linearity properties of the defining integral
i.e.
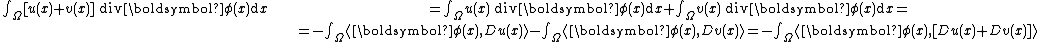
for all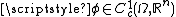
therefore 
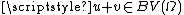for all 
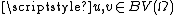, and
for all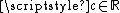
, therefore 
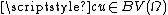for all 
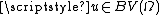, and all 
. The proved vector space
properties imply that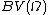
is a vector subspace of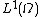 
. Consider now the function
defined as
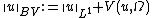
where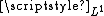
is the usual 
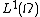norm: it is easy to prove that this is a norm
on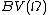
. To see that 
is complete
respect to it, i.e. it is a Banach space
, consider a Cauchy sequence
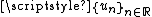in 
. By definition it is also a Cauchy sequence
in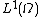
and therefore has a limit
in 
: since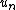 
is bounded in 
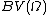for each 
, then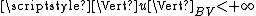 
by lower semicontinuity of the variation 
, therefore 
is a BV function. Finally, again by lower semicontinuity, choosing an arbitrary small positive number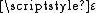 
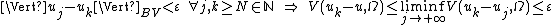
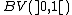: for each 0<α<1 define
as the characteristic function of the left-closed interval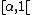
. Then, chosing α,β∈
such that α≠β the following relation holds true:
Now, in order to prove that every dense subset
of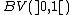
cannot be countable
, it is sufficient to see that for every α∈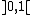
it is possible to construct the ball
s
Obviously those balls are pairwise disjoint, and also are a indexed family
of sets whose index set
is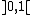
. This implies that this family has the cardinality of the continuum
: now, since any dense subset of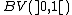
must have at least a point inside each member of this family, its cardinality is at least that of the continuum and therefore cannot a be countable subset. This example can be obviously extended to higher dimensions, and since it involves only local properties
, it implies that the same property is true for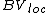
.
s for nonsmooth function
s are very important in mathematics
and mathematical physics
since there are several important physical model
s whose behavior is described by functions
or functional
s with a very limited degree of smoothness
.The following version is proved in the paper : all partial derivative
s must be intended in a generalized sense. i.e. as generalized derivatives
Theorem. Let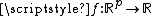
be a function of class 
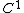(i.e. a continuous
and differentiable function
having continuous
derivative
s) and let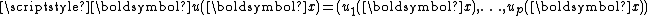
be a function in 
with 
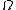being an open subset of 
.
Then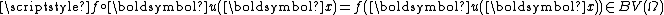
and
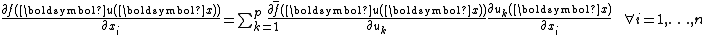
where
is the mean value of the function at the point 
, defined as
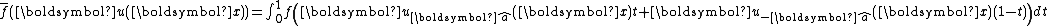
A more general chain rule
formula
for Lipschitz continuous functions
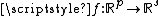has been found by Luigi Ambrosio
and Gianni Dal Maso and is published in the paper . However, even this formula has very important direct consequences: choosing
, where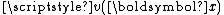 
is also a 
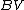function, the preceding formula gives the Leibniz rule
for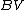
functions
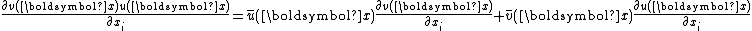
This implies that the product of two functions of bounded variation is again a function of bounded variation, therefore
is an algebra
.
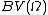is a Banach space
and also an associative algebra
: this implies that if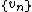
and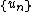 
are Cauchy sequence
s of
functions converging respectively to function
s
and 
in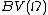 
, then
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a function of bounded variation, also known as a BV function, is a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
whose total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
is bounded (finite): the graph of a function
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
having this property is well behaved in a precise sense. For a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
of a single variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
, being of bounded variation means that the distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
along the direction
Direction (geometry, geography)
Direction is the information contained in the relative position of one point with respect to another point without the distance information. Directions may be either relative to some indicated reference , or absolute according to some previously agreed upon frame of reference Direction is the...
of the y-axis, neglecting the contribution of motion along x-axis, traveled by a point moving along the graph has a finite value. For a continuous function of several variables, the meaning of the definition is the same, except for the fact that the continuous path to be considered cannot be the whole graph of the given function (which is an hypersurface in this case), but can be every intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of the graph itself with a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
(in the case of functions of two variables, a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
) parallel to a fixed x-axis and to the y-axis.
Functions of bounded variation are precisely those with respect to which one may find Riemann–Stieltjes integrals of all continuous functions.
Another characterization states that the functions of bounded variation on a closed interval are exactly those f which can be written as a difference g − h, where both g and h are bounded monotone
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
.
In the case of several variables, a function f defined on an open subset
of ℝn is said to have bounded variation if its distributional derivativeDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
is a finite vector
Vector-valued function
A vector-valued function also referred to as a vector function is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector...
Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
.
One of the most important aspects of functions of bounded variation is that they form an algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
of discontinuous functions
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
whose first derivative exists almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
: due to this fact, they can and frequently are used to define generalized solutions of nonlinear problems involving functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
s, ordinary
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
and partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
. Considering the problem of multiplication of distributions or more generally the problem of defining general nonlinear operations on generalized function
Generalized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
s, function of bounded variation are the smallest algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
which has to be embedded in every space of generalized function
Generalized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
s preserving the result of multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
.
History
According to Boris Golubov, BV functions of a single variable were first introduced by Camille JordanCamille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
, in the paper dealing with the convergence of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. The first successful step in the generalization of this concept to functions of several variables was due to Leonida Tonelli
Leonida Tonelli
Leonida Tonelli was an Italian mathematician, most noted for creating Tonelli's theorem, usually considered a forerunner to Fubini's theorem.-External links:...
, who introduced a class of continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
BV functions in 1926 , to extend his direct method for finding solutions to problems in the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
in more than one variable. Ten years after, in , Lamberto Cesari
Lamberto Cesari
Lamberto Cesari was an Italian mathematician naturalized in the United States.- Biography :...
changed the continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
requirement in Tonelli's definition to a less restrictive integrability
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
requirement, obtaining for the first time the class of functions of bounded variation of several variables in its full generality: as Jordan did before him, he applied the concept to resolve of a problem concerning the convergence of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, but for functions of two variables. After him, several authors applied BV functions to study Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
in several variables, geometric measure theory
Geometric measure theory
In mathematics, geometric measure theory is the study of the geometric properties of the measures of sets , including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets...
, calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
, and mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
. Renato Caccioppoli
Renato Caccioppoli
Renato Caccioppoli was an Italian mathematician.- Biography :Born in Naples, Campania, he was the son of Giuseppe Caccioppoli , a surgeon, and his second wife Sofia Bakunin , daughter of the Russian revolutionary Mikhail Bakunin. After earning his diploma in 1921, he enrolled in the department of...
and Ennio de Giorgi
Ennio de Giorgi
-References:. The first paper about SBV functions and related variational problems.. The first note published by De Giorgi describing his approach to Caccioppoli sets.. The first complete exposition by De Giorgi of the theory of Caccioppoli sets.. An advanced text, oriented to the theory of minimal...
used them to define measure of non smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
boundaries
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of sets (see the entry "Caccioppoli set
Caccioppoli set
In mathematics, a Caccioppoli set is a set whose boundary is measurable and has a finite measure. A synonym is set of finite perimeter...
" for further informations). Olga Arsenievna Oleinik
Olga Arsenievna Oleinik
Olga Arsenievna Oleinik was a Soviet mathematician who conducted pioneering work on the theory of partial differential equations, the theory of strongly inhomogeneous elastic media, and the mathematical theory of boundary layers. She was a student of Ivan Petrovsky...
introduced her view of generalized solutions for nonlinear partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s as functions from the space BV in the paper , and was able to construct a generalized solution of bounded variation of a first order partial differential equation in the paper : few years later, Edward D. Conway and Joel A. Smoller applied BV-functions to the study of a single nonlinear hyperbolic partial differential equation of first order in the paper , proving that the solution of the Cauchy problem
Cauchy problem
A Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions which are given on a hypersurface in the domain. Cauchy problems are an extension of initial value problems and are to be contrasted with boundary value problems...
for such equations is a function of bounded variation, provided the initial value
Cauchy boundary condition
In mathematics, a Cauchy boundary condition imposed on an ordinary differential equation or a partial differential equation specifies both the values a solution of a differential equation is to take on the boundary of the domain and the normal derivative at the boundary. It corresponds to imposing...
belongs to the same class. Aizik Isaakovich Vol'pert
Aizik Isaakovich Vol'pert
Aizik Isaakovich Vol'pert was a Soviet mathematician and chemical engineer working in partial differential equations, functions of bounded variation and chemical kinetics.- Work :...
developed extensively a calculus for BV functions: in the paper he proved the chain rule for BV functions and in the book he, jointly with his pupil Sergei Ivanovich Hudjaev, explored extensively the properties of BV functions and their application. His chain rule formula was later extended by Luigi Ambrosio
Luigi Ambrosio
Luigi Ambrosio is a professor at Scuola Normale Superiore in Pisa, Italy.His main fields of research are the calculus of variations and geometric measure theory....
and Gianni Dal Maso in the paper .
BV functions of one variable
The total variation of a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued (or more generally complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued) function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
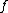, defined on an intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[a , b]⊂ℝ is the quantity
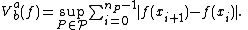
where the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
is taken over the set
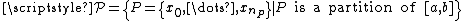of all partitionsPartition of an interval
In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
of the interval considered.
If
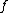is differentiableDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
and its derivative is Riemann-integrable, its total variation is the vertical component of the arc-length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
of its graph, that is to say,
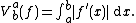
A real-valued function
on the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
is said to be of bounded variation (BV function) on a chosen interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
⊂ℝ if its total variation is finite, i.e.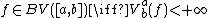It can be proved that a real function ƒ is of bounded variation in an interval if and only if it can be written as the difference ƒ = ƒ1 − ƒ2 of two non-decreasing functions: this result is known as the Jordan decomposition
Jordan decomposition
In mathematics, Jordan decomposition may refer to* Hahn decomposition theorem, and the Jordan decomposition of a measure* Jordan normal form of a matrix* Jordan–Chevalley decomposition of a matrix...
.
Through the Stieltjes integral, any function of bounded variation on a closed interval [a, b] defines a bounded linear functional on C([a, b]). In this special case, the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
states that every bounded linear functional arises uniquely in this way. The normalised positive functionals or probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s correspond to positive non-decreasing lower semicontinuous functions. This point of view has been important in
spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
, in particular in its application to ordinary differential equations
Spectral theory of ordinary differential equations
In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation...
.
BV functions of several variables
Functions of bounded variation, BV functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, are functions whose distributional derivative
Directional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
is a finite Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
. More precisely:
Let
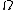be an open subset of ℝn. A function belonging to Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
is said of bounded variation (BV function), and write
if there exists a finite vector Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
such that the following equality holdsthat is,
defines a linear functionalLinear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on the space
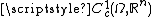of continuously differentiableSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
vector functions
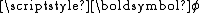of compact support contained in 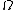: the vector measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
represents therefore the distributional or weakWeak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of
.An equivalent definition is the following.
Given a function
belonging to , the total variation of in is defined aswhere
is the essential supremum normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
. Sometimes, especially in the theory of Caccioppoli set
Caccioppoli set
In mathematics, a Caccioppoli set is a set whose boundary is measurable and has a finite measure. A synonym is set of finite perimeter...
s, the following notation is used
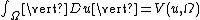
in order to emphasize that
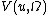is the total variation of the distributional / weakWeak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of
. This notation reminds also that if is of class 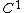(i.e. a continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
having continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s) then its variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
is exactly the integral of the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of its gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
.
The space of functions of bounded variation (BV functions) can then be defined as
The two definitions are equivalent since if
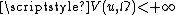thentherefore
defines a continuous linear functional onthe space
. Since 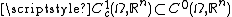as a linear subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
, this continuous linear functional can be extended continuously
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and linearily to the whole
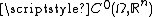by the Hahn–Banach theoremHahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
i.e. it defines a Radon measure.
Locally BV functions
If the function spaceFunction space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
of locally integrable function
Locally integrable function
In mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
s, i.e. function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s belonging to
, is considered in the preceding definitions , and instead of the one of globally integrable functions, then the function space defined is that of functions of locally bounded variation. Precisely, developing this idea for , a localLocal property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
variation is defined as follows,
for every set
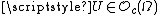, having defined 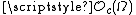as the set of all precompactRelatively compact subspace
In mathematics, a relatively compact subspace Y of a topological space X is a subset whose closure is compact....
open subsets of
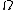with respect to the standard topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of finite dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, and correspondingly the class of functions of locally bounded variation is defined as
Notation
There are basically two distinct conventions for the notation of spaces of functions of locally or globally bounded variation, and unfortunately they are quite similar: the first one, which is the one adopted in this entry, is used for example in references (partially), (partially), and is the following one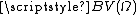
identifies the space of functions of globally bounded variation
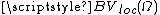identifies the space of functions of locally bounded variation
The second one, which is adopted in references and (partially), is the following:
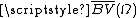identifies the space of functions of globally bounded variation
identifies the space of functions of locally bounded variation
Basic properties
Only the properties common to functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s of one variable and to function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s of several variables will be considered in the following, and proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
s will be carried on only for functions of several variables since the proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
for the case of one variable is a straightforward adaptation of the several variables case: also, in each section it will be stated if the property is shared also by functions of locally bounded variation or not. References , and are extensively used.
BV functions have only jump-type discontinuities
In the case of one variable, the assertion is clear: for each point in the intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
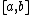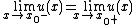
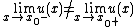
⊂ℝ of definition of the function , either one of the following two assertions is truewhile both limits
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
exist and are finite. In the case of functions of several variables, there are some premises to understand: first of all, there is a continuum
Linear continuum
In the mathematical field of order theory, a continuum or linear continuum is a generalization of the real line.Formally, a linear continuum is a linearly ordered set S of more than one element that is densely ordered, i.e., between any two members there is another, and which "lacks gaps" in the...
of direction
Direction (geometry, geography)
Direction is the information contained in the relative position of one point with respect to another point without the distance information. Directions may be either relative to some indicated reference , or absolute according to some previously agreed upon frame of reference Direction is the...
s along which it is possible to approach a given point
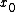belonging to the domain ⊂ℝn. It is necessary to make precise a suitable concept of limitLimit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
: choosing a unit vector
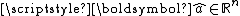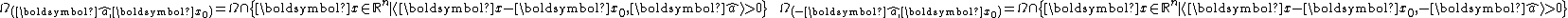
it is possible to divide in two setsThen for each point
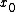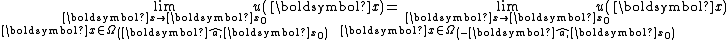
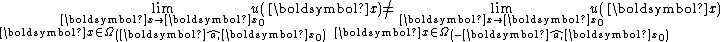
belonging to the domain of the BV function , only one of the following two assertions is trueor
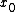belongs to a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of
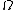having zero -dimensional Hausdorff measureHausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
. The quantities
are called approximate limits of the BV function
at the point 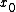.V(·, Ω) is lower semi-continuous on BV(Ω)
The functionalFunctional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
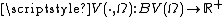is lower semi-continuousSemi-continuity
In mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...
:
to see this, choose a Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
of BV-functions
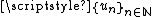converging to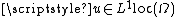 Locally integrable function
In mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
. Then, since all the functions of the sequence and their limit function are integrable
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
and by the definition of lower limit
Now considering the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
on the set of functions
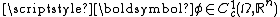such that 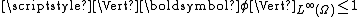then the following inequality holds truewhich is exactly the definition of lower semicontinuity.
BV(Ω) is a Banach space
By definition is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of
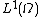, while linearity follows from the linearity properties of the defining integralIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
i.e.
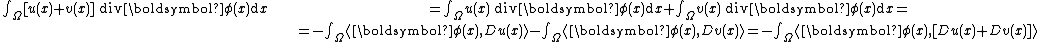
for all
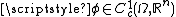therefore 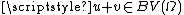for all 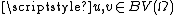, andfor all
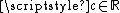, therefore 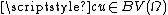for all 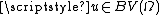, and all . The proved vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
properties imply that
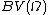is a vector subspace of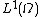 Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. Consider now the function
defined as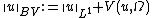where
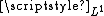is the usual 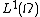norm: it is easy to prove that this is a normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
on
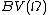. To see that is completeCompleteness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
respect to it, i.e. it is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, consider a Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
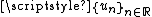in . By definition it is also a Cauchy sequenceCauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
in
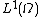and therefore has a limitLimit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
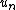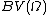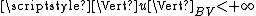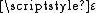
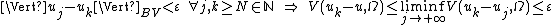
in : since is bounded in for each , then by lower semicontinuity of the variation , therefore is a BV function. Finally, again by lower semicontinuity, choosing an arbitrary small positive number BV(Ω) is not separable
To see this, it is sufficient to consider the following example belonging to the space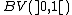: for each 0<α<1 defineas the characteristic function of the left-closed interval
. Then, chosing α,β∈ such that α≠β the following relation holds true:Now, in order to prove that every dense subset
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
of
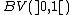cannot be countableCountable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
, it is sufficient to see that for every α∈
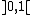it is possible to construct the ballBall (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
s
Obviously those balls are pairwise disjoint, and also are a indexed family
Indexed family
In mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
of sets whose index set
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
is
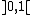. This implies that this family has the cardinality of the continuumCardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
: now, since any dense subset of
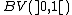must have at least a point inside each member of this family, its cardinality is at least that of the continuum and therefore cannot a be countable subset. This example can be obviously extended to higher dimensions, and since it involves only local propertiesLocal property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
, it implies that the same property is true for
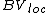.Chain rule for BV functions
Chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
s for nonsmooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s are very important in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
since there are several important physical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
s whose behavior is described by functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
or functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
s with a very limited degree of smoothness
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
.The following version is proved in the paper : all partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s must be intended in a generalized sense. i.e. as generalized derivatives
Theorem. Let
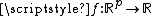be a function of class 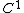(i.e. a continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
having continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s) and let
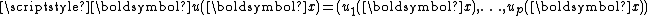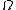be a function in with being an open subset of .Then
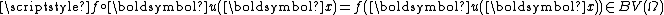and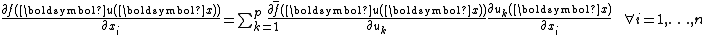where
is the mean value of the function at the point , defined as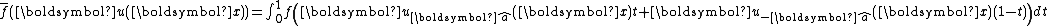A more general chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
for Lipschitz continuous functions
Lipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
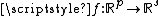has been found by Luigi AmbrosioLuigi Ambrosio
Luigi Ambrosio is a professor at Scuola Normale Superiore in Pisa, Italy.His main fields of research are the calculus of variations and geometric measure theory....
and Gianni Dal Maso and is published in the paper . However, even this formula has very important direct consequences: choosing
, where 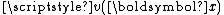is also a 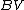function, the preceding formula gives the Leibniz ruleProduct rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
for
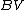functions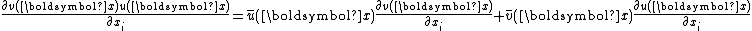This implies that the product of two functions of bounded variation is again a function of bounded variation, therefore
is an algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
.
BV(Ω) is a Banach algebra
This property follows directly from the fact that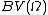 is a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
and also an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
: this implies that if
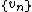and 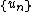are Cauchy sequenceCauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s of
functions converging respectively to functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s
and in 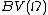, then-
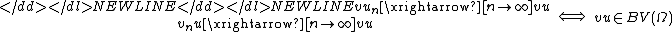
therefore the ordinary product of functionsPointwise productThe pointwise product of two functions is another function, obtained by multiplying the image of the two functions at each value in the domain...
is continuous in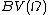
respect to each argument, making this function space a Banach algebraBanach algebraIn mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
.
Weighted BV functions
It is possible to generalize the above notion of total variationTotal variationIn mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
so that different variations are weighted differently. More precisely, let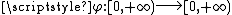
be any increasing function such that 
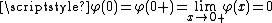(the weight functionWeight functionA weight function is a mathematical device used when performing a sum, integral, or average in order to give some elements more "weight" or influence on the result than other elements in the same set. They occur frequently in statistics and analysis, and are closely related to the concept of a...
) and let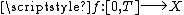
be a function from the intervalInterval (mathematics)In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
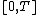⊂ℝ taking values in a normed vector spaceNormed vector spaceIn mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
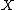. Then the 
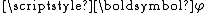-variation of 
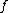over 
is defined as
where, as usual, the supremum is taken over all finite partitionsPartition of an intervalIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
of the interval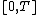
, i.e. all the finite sets of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s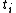
such that
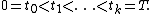
The original notion of variationTotal variationIn mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
considered above is the special case of
-variation for which the weight function is the identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
: therefore an integrable function
is said to be a weighted BV function (of weight 
) if and only if its 
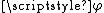-variation is finite.
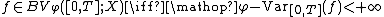
The space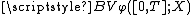
is a topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
with respect to the normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
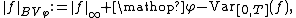
where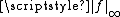
denotes the usual supremum norm of 
. Weighted BV functions were introduced and studied in full generality by Władysław Orlicz and Julian Musielak in the paper : Laurence Chisholm YoungLaurence Chisholm YoungLaurence Chisholm Young was a mathematician known for his contributions to measure theory, the calculus of variations, optimal control theory, and potential theory...
studied earlier the case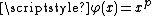
where 
is a positive integer.
SBV functions
SBV functions i.e. Special functions of Bounded Variation where introduced by Luigi AmbrosioLuigi AmbrosioLuigi Ambrosio is a professor at Scuola Normale Superiore in Pisa, Italy.His main fields of research are the calculus of variations and geometric measure theory....
and Ennio de GiorgiEnnio de Giorgi-References:. The first paper about SBV functions and related variational problems.. The first note published by De Giorgi describing his approach to Caccioppoli sets.. The first complete exposition by De Giorgi of the theory of Caccioppoli sets.. An advanced text, oriented to the theory of minimal...
in the paper , dealing with free discontinuity variational problems: given an open subset
of ℝn, the space 
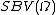is a proper subspaceSubspace-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
of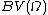
, since the weakWeak derivativeIn mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of each function belonging to it const exactly of the sumSUMSUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...
of a
-dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al supportSupport (mathematics)In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
and a
-dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al supportSupport (mathematics)In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
measureMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
and no intermediate-dimensional terms, as seen in the following definition.
Definition. Given a locally integrable functionLocally integrable functionIn mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
, then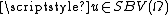 
if and only if
1. There exist two Borel functions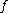
and 
of domainDomain (mathematics)In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
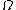and codomainCodomainIn mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
ℝn such that
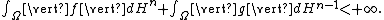
2. For all of continuously differentiableSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
vector functions
of compact support contained in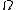 
, i.e. for all 
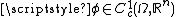the following formula is true:
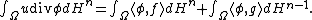
where
is the 
-dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Hausdorff measureHausdorff measureIn mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
.
Details on the properties of SBV functions can be found in works cited in the bibliography section: particularly the paper contains a useful bibliographyBibliographyBibliography , as a practice, is the academic study of books as physical, cultural objects; in this sense, it is also known as bibliology...
.
bv sequences
As particular examples of Banach spaces, consider spaces of sequences of bounded variation, in addition to the spaces of functions of bounded variation. The total variation of a sequence x=(xi) of real or complex numbers is defined by
The space of all sequences of finite total variation is denoted by bv. The norm on bv is given by
With this norm, the space bv is a Banach space.
The total variation itself defines a norm on a certain subspace of bv, denoted by bv0, consisting of sequences x = (xi) for which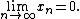
The norm on bv0 is denoted
With respect to this norm bv0 becomes a Banach space as well.
Measures of bounded variation
A signedSigned measureIn mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
(or complexComplex measureIn mathematics, specifically measure theory, a complex measure generalizes the concept of measure by letting it have complex values. In other words, one allows for sets whose size is a complex number.-Definition:...
) measureMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on a measurable spaceSigma-algebraIn mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
is said to be of bounded variation if its total variation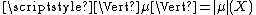 
is bounded: see , or the entry "Total variationTotal variationIn mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
" for further details.
Examples
The function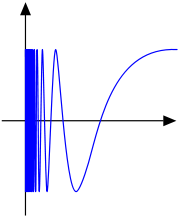
is not of bounded variation on the interval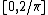
While it is harder to see, the function.svg.png)
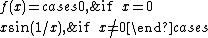
is not of bounded variation on the interval
either.
At the same time, the function.svg.png)
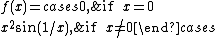
is of bounded variation on the interval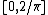
. However, all three functions are of bounded variation on each interval 
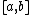with 
.
The Sobolev spaceSobolev spaceIn mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
is a proper subset of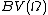 
. In fact, for each 
in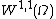 
it is possible to choose a measureMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
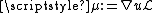(where 
is the Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on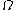
) such that the equality
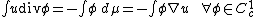
holds, since it is nothing more than the definition of weak derivativeWeak derivativeIn mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
, and hence holds true. One can easily find an example of a BV function which is not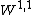
: in dimension one, any step function with a non-trivial jump will do.
Mathematics
Functions of bounded variation have been studied in connection with the set of discontinuitiesClassification of discontinuitiesContinuous functions are of utmost importance in mathematics and applications. However, not all functions are continuous. If a function is not continuous at a point in its domain, one says that it has a discontinuity there...
of functions and differentiability of real functions, and the following results are well-known. If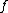
is a realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of bounded variation on an interval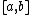
then
-
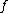is continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
except at most on a countable setCountable setIn mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
; -
has one-sided limitOne-sided limitIn calculus, a one-sided limit is either of the two limits of a function f of a real variable x as x approaches a specified point either from below or from above...
s everywhere (limits from the left everywhere in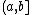
, and from the right everywhere in 
; - the derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
exists almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
(i.e. except for a set of measure zero).
For realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
functionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of several real variables
- the characteristic function of a Caccioppoli setCaccioppoli setIn mathematics, a Caccioppoli set is a set whose boundary is measurable and has a finite measure. A synonym is set of finite perimeter...
is a BV function: BV functions lie at the basis of the modern theory of perimeters. - Minimal surfaceMinimal surfaceIn mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
s are graphGraph of a functionIn mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
s of BV functions: in this context, see reference .
Physics and engineering
The ability of BV functions to deal with discontinuities has made their use widespread in the applied sciences: solutions of problems in mechanics, physics, chemical kinetics are very often representable by functions of bounded variation. The book details a very ample set of mathematical physics applications of BV functions. Also there is some modern application which deserves a brief description.
- The Mumford-Shah functional: the segmentation problem for a two-dimensional image, i.e. the problem of faithful reproduction of contours and grey scales is equivalent to the minimization of such functionalFunctional (mathematics)In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
.
Other
- Luigi Ambrosio home page at the Scuola Normale Superiore, PisaPisaPisa is a city in Tuscany, Central Italy, on the right bank of the mouth of the River Arno on the Tyrrhenian Sea. It is the capital city of the Province of Pisa...
. Academic home page (with preprints and publications) of one of the contributors to the theory and applications of BV functions. - Research Group in Calculus of Variations and Geometric Measure Theory, Scuola Normale Superiore, PisaPisaPisa is a city in Tuscany, Central Italy, on the right bank of the mouth of the River Arno on the Tyrrhenian Sea. It is the capital city of the Province of Pisa...
.
-----