
Signed measure
Encyclopedia
In mathematics
, signed measure is a generalization of the concept of measure
by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge
, which is a familiar distribution that takes on positive and negative values.
Given a measurable space (X, Σ), that is, a set X with a sigma algebra Σ on it, an extended signed measure is a function

such that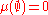 and
and  is sigma additive
is sigma additive
, that is, it satisfies the equality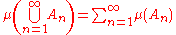
for any sequence
A1, A2, ..., An, ... of disjoint sets in Σ. One consequence is that any extended signed measure can take +∞ as value, or it can take −∞ as value, but both are not available. The expression ∞ − ∞ is undefined (see Extended real number line) and must be avoided.
A finite signed measure is defined in the same way, except that it is only allowed to take real values. That is, it cannot take +∞ or −∞.
Finite signed measures form a vector space, while extended signed measures are not even closed under addition, which makes them rather hard to work with. On the other hand, measures are extended signed measures, but are not in general finite signed measures.
f:X→ R such that
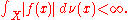
Then, a finite signed measure is given by
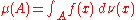
for all A in Σ.
This signed measure takes only finite values. To allow it to take +∞ as a value, one needs to replace the assumption about f being absolutely integrable with the more relaxed condition
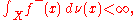
where f−(x) = max(−f(x), 0) is the negative part of f.
The Hahn decomposition theorem
states that given a signed measure μ, there exist two measurable sets P and N such that:
Moreover, this decomposition is unique up to
adding to/subtracting μ-null set
s from P and N.
Consider then two nonnegative measures μ+ and μ- defined by
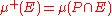
and

for all measurable sets E, that is, E in Σ.
One can check that both μ+ and μ- are nonnegative measures, with one taking only finite values, and are called the positive part and negative part of μ, respectively. One has that μ = μ+ - μ-. The measure |μ| = μ+ + μ- is called the variation of μ, and its maximum possible value, ||μ|| = |μ|(X), is called the total variation
of μ.
This consequence of the Hahn decomposition theorem is called the Jordan decomposition. The measures μ+, μ- and |μ| are independent of the choice of P and N in the Hahn decomposition theorem.
. It follows that the set of finite signed measures on a measure space (X, Σ) is a real vector space
; this is in contrast to positive measures, which are only closed under conical combination
, and thus form a convex cone
but not a vector space. Furthermore, the total variation
defines a norm
in respect to which the space of finite signed measures becomes a Banach space
.
If X is a compact separable space, then the space of finite signed Baire measures is the dual of the real Banach space of all continuous real-valued functions on X, by the Riesz representation theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, signed measure is a generalization of the concept of measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
, which is a familiar distribution that takes on positive and negative values.
Definition
There are two slightly different concepts of a signed measure, depending on whether or not one allows it to take infinite values. In research papers and advanced books signed measures are usually only allowed to take finite values, while undergraduate textbooks often allow them to take infinite values. To avoid confusion, this article will call these two cases "finite signed measures" and "extended signed measures".Given a measurable space (X, Σ), that is, a set X with a sigma algebra Σ on it, an extended signed measure is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

such that
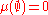 and
and  is sigma additive
is sigma additiveSigma additivity
In mathematics, additivity and sigma additivity of a function defined on subsets of a given set are abstractions of the intuitive properties of size of a set.- Additive set functions :...
, that is, it satisfies the equality
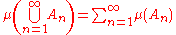
for any sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
A1, A2, ..., An, ... of disjoint sets in Σ. One consequence is that any extended signed measure can take +∞ as value, or it can take −∞ as value, but both are not available. The expression ∞ − ∞ is undefined (see Extended real number line) and must be avoided.
A finite signed measure is defined in the same way, except that it is only allowed to take real values. That is, it cannot take +∞ or −∞.
Finite signed measures form a vector space, while extended signed measures are not even closed under addition, which makes them rather hard to work with. On the other hand, measures are extended signed measures, but are not in general finite signed measures.
Examples
Consider a nonnegative measure ν on the space (X, Σ) and a measurable functionMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
f:X→ R such that
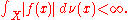
Then, a finite signed measure is given by
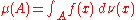
for all A in Σ.
This signed measure takes only finite values. To allow it to take +∞ as a value, one needs to replace the assumption about f being absolutely integrable with the more relaxed condition
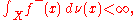
where f−(x) = max(−f(x), 0) is the negative part of f.
Properties
What follows are two results which will imply that an extended signed measure is the difference of two nonnegative measures, and a finite signed measure is the difference of two finite non-negative measures.The Hahn decomposition theorem
Hahn decomposition theorem
In mathematics, the Hahn decomposition theorem, named after the Austrian mathematician Hans Hahn, states that given a measurable space and a signed measure μ defined on the σ-algebra Σ, there exist two sets P and N in Σ such that:...
states that given a signed measure μ, there exist two measurable sets P and N such that:
- P∪N = X and P∩N = ∅;
- μ(E) ≥ 0 for each E in Σ such that E ⊆ P — in other words, P is a positive setPositive and negative setsIn measure theory, given a measurable space and a signed measure μ on it, a set A ∈ Σ is called a positive set for μ if every Σ-measurable subset of A has nonnegative measure; that is, for every E ⊆ A that satisfies E ∈ Σ, one has μ ≥ 0.Similarly, a set A ∈ Σ is called a negative set for μ if for...
; - μ(E) ≤ 0 for each E in Σ such that E ⊆ N — that is, N is a negative set.
Moreover, this decomposition is unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
adding to/subtracting μ-null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
s from P and N.
Consider then two nonnegative measures μ+ and μ- defined by
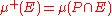
and

for all measurable sets E, that is, E in Σ.
One can check that both μ+ and μ- are nonnegative measures, with one taking only finite values, and are called the positive part and negative part of μ, respectively. One has that μ = μ+ - μ-. The measure |μ| = μ+ + μ- is called the variation of μ, and its maximum possible value, ||μ|| = |μ|(X), is called the total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
of μ.
This consequence of the Hahn decomposition theorem is called the Jordan decomposition. The measures μ+, μ- and |μ| are independent of the choice of P and N in the Hahn decomposition theorem.
The space of signed measures
The sum of two finite signed measures is a finite signed measure, as is the product of a finite signed measure by a real number: they are closed under linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
. It follows that the set of finite signed measures on a measure space (X, Σ) is a real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
; this is in contrast to positive measures, which are only closed under conical combination
Conical combination
Given a finite number of vectors x_1, x_2, \dots, x_n\, in a real vector space, a conical combination or a conical sum of these vectors is a vector of the formwhere the real numbers \alpha_i\, satisfy \alpha_i\ge 0...
, and thus form a convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
but not a vector space. Furthermore, the total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
defines a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
in respect to which the space of finite signed measures becomes a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
.
If X is a compact separable space, then the space of finite signed Baire measures is the dual of the real Banach space of all continuous real-valued functions on X, by the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
.
See also
- Complex measureComplex measureIn mathematics, specifically measure theory, a complex measure generalizes the concept of measure by letting it have complex values. In other words, one allows for sets whose size is a complex number.-Definition:...
- Spectral measure
- Vector measureVector measureIn mathematics, a vector measure is a function defined on a family of sets and taking vector values satisfying certain properties. It is a generalization of the concept of measure, which takes nonnegative real values only.-Definitions and first consequences:...
- Riesz representation theoremRiesz representation theoremThere are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
- Total variationTotal variationIn mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...

