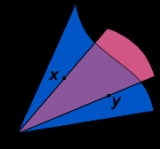
Convex cone
Encyclopedia
In linear algebra
, a convex cone is a subset
of a vector space
over an ordered field
that is closed
under linear combination
s with positive coefficients.
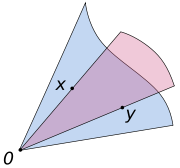
The defining condition can be written more succinctly as "αC + βC = C" for any positive scalars α, β.
The concept is meaningful for any vector space that allows the concept of "positive" scalar, such as spaces over the rational
, algebraic
, or (more commonly) the real number
s.
The empty set, the space V, and any linear subspace of V (including the trivial subspace {0}) are convex cones by this definition. Other examples are the set of all positive multiples of an arbitrary vector v of V, or the positive orthant
of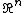
(the set of all vectors whose coordinates are all positive).
A more general example is the set of all vectors λx such that λ is a positive scalar and x is an element of some convex subset
X of V. In particular, if V is a normed vector space
, and X is an open (resp. closed) ball
of V that does not contain 0, this construction gives an open (resp. closed) convex circular cone.
The intersection of two convex cones in the same vector space is again a convex cone, but their union may fail to be one. The class
of convex cones is also closed under arbitrary linear maps. In particular, if C is a convex cone, so is its opposite -C; and C
(-C) is the largest linear subspace contained in C.
.
s, or just under addition
s. More succinctly, a set C is a convex cone if and only if "αC = C and C + C = C, for any positive scalar α of V.
It follows also that one can replace the phrase "positive scalars α, β" in the definition of convex cone by "non-negative scalars α, β, not both zero".
{0} is a convex cone, too. A convex cone is said to be pointed or blunt depending on whether it includes the null vector 0 or not. Blunt cones can be excluded from the definition of convex cone by substituting "non-negative" for "positive" in the condition of α, β. The term "pointed" is also often used to refer to a closed cone that contains no complete line (i.e., no nontrivial subspace of the ambient vector space V), i.e. what is called a "salient" cone below.
0), where L is any linear function
from V to its scalar field. The hyperplane defined by L(v) = 0 is the bounding hyperplane of H.
Half-spaces (open or closed) are convex cones. Moreover, any convex cone C that is not the whole space V must be contained in some closed half-space H of V. In fact, a topologically closed convex cone is the intersection of all closed half-spaces that contain it. The analogous result holds for any topologically open convex cone.
A blunt convex cone is necessarily salient, but the converse is not necessarily true. A convex cone C is salient if and only if C
(-C)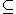
{0}; that is, if and only if C does not contain any non-trivial linear subspace of V.
A perfect half-space of V is defined recursively as follows: if V is zero-dimensional, then it is the set {0}, else it is any open half-space H of V, together with a perfect half-space of the bounding hyperplane of H.
Every perfect half-space is a salient convex cone; and, moreover, every salient convex cone is contained in a perfect half-space. In other words, the perfect half-spaces are the maximal
salient convex cones (under the containment order). In fact, it can be proved that every pointed salient convex cone (independently of whether it is topologically open, closed, or mixed) is the intersection of all the perfect half-spaces that contain it.
The following result follows from the property of containment by half-spaces. Let Q be an open half-space of V, and A = H + v where H is the bounding hyperplane of Q and v is any vector in Q. Let C be a linear cone contained in Q. Then C is a convex cone if and only the set C' = C
A is a convex subset
of A (i.e. a set closed under convex combination
s).
Because of this result, all properties of convex sets of an affine space
have an analog for the convex cones contained in a fixed open half-space.
|·| for V, we define the unit sphere
of V as the set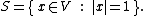
If the values of |·| are scalars of V, then a linear cone C of V is a convex cone if and only if its spherical section C'
S (the set of its unit-norm
vectors) is a convex subset of S, in the following sense: for any two vectors u, v in C' with u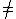
-v, all the vectors in the shortest path
from u to v in S are in C' .
be a convex cone in
a real vector space V equipped with an inner product.
The dual cone to C is the set
This is also a convex cone. If C is equal to its dual cone,
C is called self-dual.
Another common notion of the dual of a cone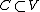
is
that it is the cone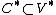
in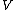 
's dual space
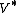defined by: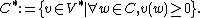
In other words, if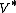
is the algebraic dual space of 
,
it is the set of linear functionals that are nonnegative on
the primal cone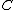
. If we take 
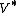to be the continuous dual space then it is the set of continuous linear functionals nonnegative on 
.
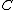This notion does not require the specification of
an inner product on
.
In finite dimensions, the two notions of dual cone are essentially the same because any inner
product induces a linear isomorphism (nonsingular linear map) from
to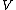
, and this isomorphism will take the dual cone given by the second
definition, in
, onto the one given by the first definition. A cone
can be said to be self-dual without reference to any given inner product, if there exists an
inner product with respect to which it is equal to its dual by the first definition. The map
from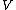
to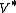 
induced by this inner product will therefore take
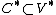to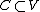 
. However, the existence of an
linear isomorphism of the dual cone onto the primal cone is not equivalent to self-duality in this sense: while every such isomorphism induces a nonsingular bilinear form on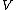
, this form is not necessarily positive definite (i.e., not necessarily an inner product). There are many examples of cones that are linearly isomorphic to their dual cones, but not self-dual: any cone in three-dimensions with a regular polygonal base having an even number of vertices is an example.
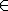C. (If the cone is flat, the same definition gives merely a preorder
.) Sums and positive scalar multiples of valid inequalities with respect to this order remain valid inequalities. A vector space with such an order is called an ordered vector space
. Examples include the product order
on real-valued vectors (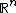
) and the Loewner order on matrices.
"cone" for what this article calls a salient pointed cone or for one of the notions of proper cone
just described.
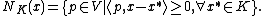
Given a closed, convex subset K of V, the tangent cone (or contingent cone) to the set K at the point x is given by
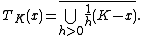
Both the normal and tangent cone have the property of being closed and convex. They are important concepts in the fields of convex optimization, variational inequalities
and projected dynamical system
s.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a convex cone is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
that is closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s with positive coefficients.
Definition
A subset C of a vector space V is a convex cone if αx + βy belongs to C, for any positive scalars α, β , and any x, y in C.The defining condition can be written more succinctly as "αC + βC = C" for any positive scalars α, β.
The concept is meaningful for any vector space that allows the concept of "positive" scalar, such as spaces over the rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
, algebraic
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
, or (more commonly) the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s.
The empty set, the space V, and any linear subspace of V (including the trivial subspace {0}) are convex cones by this definition. Other examples are the set of all positive multiples of an arbitrary vector v of V, or the positive orthant
Orthant
In geometry, an orthant or hyperoctant is the analogue in n-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions....
of
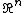(the set of all vectors whose coordinates are all positive).A more general example is the set of all vectors λx such that λ is a positive scalar and x is an element of some convex subset
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
X of V. In particular, if V is a normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
, and X is an open (resp. closed) ball
Ball
A ball is a round, usually spherical but sometimes ovoid, object with various uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used for simpler activities, such as catch, marbles and juggling...
of V that does not contain 0, this construction gives an open (resp. closed) convex circular cone.
The intersection of two convex cones in the same vector space is again a convex cone, but their union may fail to be one. The class
of convex cones is also closed under arbitrary linear maps. In particular, if C is a convex cone, so is its opposite -C; and C
(-C) is the largest linear subspace contained in C.Convex cones are linear cones
If C is a convex cone, then for any positive scalar α and any x in C the vector αx = (α/2)x + (α/2)x is in C. It follows that a convex cone C is a special case of a linear coneCone (linear algebra)
In linear algebra, a cone is a subset of a vector space that is closed under multiplication by positive scalars. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V .A cone is said...
.
Alternative definitions
It follows from the above property that a convex cone can also be defined as a linear cone that is closed under convex combinationConvex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
s, or just under addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
s. More succinctly, a set C is a convex cone if and only if "αC = C and C + C = C, for any positive scalar α of V.
It follows also that one can replace the phrase "positive scalars α, β" in the definition of convex cone by "non-negative scalars α, β, not both zero".
Blunt and pointed cones
According to the above definition, if C is a convex cone, then C{0} is a convex cone, too. A convex cone is said to be pointed or blunt depending on whether it includes the null vector 0 or not. Blunt cones can be excluded from the definition of convex cone by substituting "non-negative" for "positive" in the condition of α, β. The term "pointed" is also often used to refer to a closed cone that contains no complete line (i.e., no nontrivial subspace of the ambient vector space V), i.e. what is called a "salient" cone below.Half-spaces
A (linear) hyperplane of V is a maximal proper linear subspace of V. An open (resp. closed) half-space of V is any subset H of V defined by the condition L(x) > 0 (resp. L(x)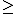0), where L is any linear functionLinear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
from V to its scalar field. The hyperplane defined by L(v) = 0 is the bounding hyperplane of H.
Half-spaces (open or closed) are convex cones. Moreover, any convex cone C that is not the whole space V must be contained in some closed half-space H of V. In fact, a topologically closed convex cone is the intersection of all closed half-spaces that contain it. The analogous result holds for any topologically open convex cone.
Salient convex cones and perfect half-spaces
A convex cone is said to be flat if it contains some nonzero vector x and its opposite -x; and salient otherwise.A blunt convex cone is necessarily salient, but the converse is not necessarily true. A convex cone C is salient if and only if C
(-C)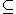{0}; that is, if and only if C does not contain any non-trivial linear subspace of V.A perfect half-space of V is defined recursively as follows: if V is zero-dimensional, then it is the set {0}, else it is any open half-space H of V, together with a perfect half-space of the bounding hyperplane of H.
Every perfect half-space is a salient convex cone; and, moreover, every salient convex cone is contained in a perfect half-space. In other words, the perfect half-spaces are the maximal
Maximal element
In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
salient convex cones (under the containment order). In fact, it can be proved that every pointed salient convex cone (independently of whether it is topologically open, closed, or mixed) is the intersection of all the perfect half-spaces that contain it.
Flat section
An affine hyperplane of V is any subset of V of the form v + H, where v is a vector of V and H is a (linear) hyperplane.The following result follows from the property of containment by half-spaces. Let Q be an open half-space of V, and A = H + v where H is the bounding hyperplane of Q and v is any vector in Q. Let C be a linear cone contained in Q. Then C is a convex cone if and only the set C' = C
A is a convex subsetConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
of A (i.e. a set closed under convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
s).
Because of this result, all properties of convex sets of an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
have an analog for the convex cones contained in a fixed open half-space.
Spherical section
Given a normNormed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
|·| for V, we define the unit sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
of V as the set
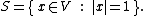
If the values of |·| are scalars of V, then a linear cone C of V is a convex cone if and only if its spherical section C'
S (the set of its unit-normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
vectors) is a convex subset of S, in the following sense: for any two vectors u, v in C' with u
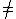-v, all the vectors in the shortest pathGeodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
from u to v in S are in C' .
Dual cone
Let be a convex cone ina real vector space V equipped with an inner product.
The dual cone to C is the set
This is also a convex cone. If C is equal to its dual cone,
C is called self-dual.
Another common notion of the dual of a cone
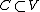isthat it is the cone
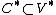in 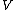's dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
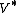defined by: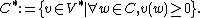In other words, if
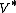is the algebraic dual space of ,it is the set of linear functionals that are nonnegative on
the primal cone
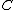. If we take 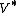to be the continuous dual space then it is the set of continuous linear functionals nonnegative on 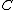.This notion does not require the specification of
an inner product on
.In finite dimensions, the two notions of dual cone are essentially the same because any inner
product induces a linear isomorphism (nonsingular linear map) from
to
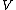, and this isomorphism will take the dual cone given by the seconddefinition, in
, onto the one given by the first definition. A conecan be said to be self-dual without reference to any given inner product, if there exists an
inner product with respect to which it is equal to its dual by the first definition. The map
from
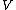to 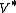induced by this inner product will therefore take 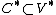to 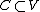. However, the existence of anlinear isomorphism of the dual cone onto the primal cone is not equivalent to self-duality in this sense: while every such isomorphism induces a nonsingular bilinear form on
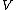, this form is not necessarily positive definite (i.e., not necessarily an inner product). There are many examples of cones that are linearly isomorphic to their dual cones, but not self-dual: any cone in three-dimensions with a regular polygonal base having an even number of vertices is an example.Partial order defined by a convex cone
A pointed and salient convex cone cone C induces a partial ordering "≤" on V, defined so that x≤y if and only if y − x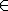 C. (If the cone is flat, the same definition gives merely a preorderPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
.) Sums and positive scalar multiples of valid inequalities with respect to this order remain valid inequalities. A vector space with such an order is called an ordered vector space
Ordered vector space
In mathematics an ordered vector space or partially ordered vector space is a vector space equipped with a partial order which is compatible with the vector space operations.- Definition:...
. Examples include the product order
Product order
In mathematics, given two ordered sets A and B, one can induce a partial ordering on the Cartesian product A × B. Giventwo pairs and in A × B, one sets ≤...
on real-valued vectors (
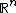) and the Loewner order on matrices. Proper convex cone
The term proper (convex) cone is variously defined, depending on the context. It often means a salient convex cone that is not contained in any hyperplane of V, possibly with other conditions such as topologically closed (and hence pointed), or topologically open (and hence blunt). Some authors use the term "wedge" for what this article calls a convex cone, and reserve"cone" for what this article calls a salient pointed cone or for one of the notions of proper cone
just described.
Examples of convex cones
Given a closed, convex subset K of V, the normal cone to the set K at the point x in K is given by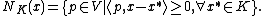Given a closed, convex subset K of V, the tangent cone (or contingent cone) to the set K at the point x is given by
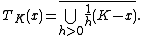
Both the normal and tangent cone have the property of being closed and convex. They are important concepts in the fields of convex optimization, variational inequalities
Variational inequality
In mathematics, a variational inequality is an inequality involving a functional, which has to be solved for all the value of a given variable, belonging usually to a convex set...
and projected dynamical system
Projected dynamical system
Projected dynamical systems is a mathematical theory investigating the behaviour of dynamical systems where solutions are restricted to a constraint set. The discipline shares connections to and applications with both the static world of optimization and equilibrium problems and the dynamical world...
s.
See also
- Cone (disambiguation)
- Cone (geometry)Cone (geometry)A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
- Cone (topology)Cone (topology)In topology, especially algebraic topology, the cone CX of a topological space X is the quotient space:CX = /\,of the product of X with the unit interval I = [0, 1]....
- Cone (linear algebra)Cone (linear algebra)In linear algebra, a cone is a subset of a vector space that is closed under multiplication by positive scalars. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V .A cone is said...
- Cone (geometry)
- Farkas' lemma
Related combinations
- Affine combination
- Convex combinationConvex combinationIn convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
- Linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...