Null vector (vector space)
Encyclopedia
In linear algebra
, the null vector or zero vector or empty vector is the vector (0, 0, …, 0) in Euclidean space
, all of whose components are zero. It is usually written with an arrow head above or below it :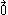
or 0 or simply 0. A zero vector has arbitrary direction, but is orthogonal (ie perpendicular, normal) to all other vectors with the same number of components.
A different kind of vector, also called null vector or zero vector, arises in various generalizations of Euclidean space, as explained below.
Since the word null has a more general (and very different) meaning in computer programming, many programmers prefer the term zero vector to avoid confusion. For example, the statement if ( MyVector
Linear algebra
For a general vector space
, the zero vector (or null vector)or empty vector is the uniquely determined vector that is the identity element
for vector addition.
The zero vector is unique; if a and b are zero vectors, then a = a + b = b.
The zero vector is a special case of the zero tensor. It is the result of scalar multiplication
by the scalar 0 (here meaning the additive identity of the underlying field
, not necessarily the real number 0).
The preimage of the zero vector under a linear transformation
f is called kernel
or null space
.
A zero space is a linear space whose only element is a zero vector.
The zero vector is, by itself, linearly dependent
, and so any set of vectors which includes it is also linearly dependent.
In a normed
vector space there is only one vector of norm equal to 0. This is just the zero vector.
In vector algebra its coordinates are ( 0,0 ) and its unit vector is n
Seminormed vector spaces
In a seminormed
vector space there might be more than one vector of norm equal to 0. These vectors are often called null vectors.
. In general, the coordinate representation of a null vector in Minkowski space contains non-zero values.
In the Verma module
of a Lie algebra
there are null vectors.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the null vector or zero vector or empty vector is the vector (0, 0, …, 0) in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, all of whose components are zero. It is usually written with an arrow head above or below it :
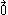or 0 or simply 0. A zero vector has arbitrary direction, but is orthogonal (ie perpendicular, normal) to all other vectors with the same number of components.A different kind of vector, also called null vector or zero vector, arises in various generalizations of Euclidean space, as explained below.
Since the word null has a more general (and very different) meaning in computer programming, many programmers prefer the term zero vector to avoid confusion. For example, the statement if ( MyVector
Null )
would intuitively be interpreted as if MyVector is a null pointer by many programmers, as opposed to if MyVector is a null/zero vector.Linear algebra
For a general vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, the zero vector (or null vector)or empty vector is the uniquely determined vector that is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
for vector addition.
The zero vector is unique; if a and b are zero vectors, then a = a + b = b.
The zero vector is a special case of the zero tensor. It is the result of scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
by the scalar 0 (here meaning the additive identity of the underlying field
Field
-Places:* Field, British Columbia, Canada* Field, Minneapolis, Minnesota, United States* Field, Ontario, Canada* Field Island, Nunavut, Canada* Mount Field - Expanses of open ground :* Field...
, not necessarily the real number 0).
The preimage of the zero vector under a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
f is called kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
or null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
.
A zero space is a linear space whose only element is a zero vector.
The zero vector is, by itself, linearly dependent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
, and so any set of vectors which includes it is also linearly dependent.
In a normed
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
vector space there is only one vector of norm equal to 0. This is just the zero vector.
In vector algebra its coordinates are ( 0,0 ) and its unit vector is n
Seminormed vector spaces
In a seminormed
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
vector space there might be more than one vector of norm equal to 0. These vectors are often called null vectors.
Examples
The light-like vectors of Minkowski spaceMinkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. In general, the coordinate representation of a null vector in Minkowski space contains non-zero values.
In the Verma module
Verma module
Verma modules, named after Daya-Nand Verma, are objects in the representation theory of Lie algebras, a branch of mathematics.The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties...
of a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
there are null vectors.