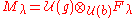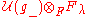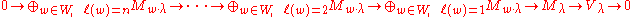Verma module
Encyclopedia
Verma modules, named after Daya-Nand Verma
, are objects in the representation theory
of Lie algebra
s, a branch of mathematics
.
The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties. Their homomorphisms correspond to invariant differential operators over flag manifold
s.
Verma modules can be used to prove that an irreducible highest weight module with highest weight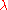
is finite dimensional
, if and only if the weight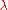
is dominant and integral.
be a field and denote the following:
To define the Verma module, we begin by defining some other modules:
Now we can define the Verma module (with respect to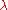
) as
which is naturally a left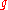
-module (i.e. an infinite-dimensional representation of 
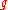). The Poincaré-Birkhoff-Witt theorem implies that the underlying vector space of 
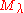is isomorphic to
where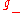
is the Lie subalgebra generated by the negative root spaces of 
.
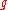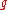-modules
, are highest weight modules, i.e. they are generated by a highest weight vector. This highest weight vector is
(the first 
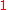is the unit in 
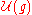and the second is
the unit in the field
, considered as the 
-module
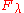) and it has weight 
.
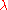Verma modules are weight modules, i.e.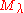
is a direct sum
of all its weight spaces. Each weight space in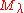
is finite dimensional and the dimension of the 
-weight space 
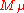is the number of possibilities how to obtain 
as a sum of positive roots (this is closely related to the so-called Kostant partition function
).
Verma modules have a very important property: If
is any representation generated by a highest weight vector of weight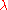 
, there is a surjective 
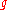-homomorphism
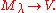That is, all representations with highest weight 
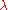that are generated by the highest weight vector (so called highest weight modules) are quotients
of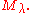
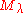contains a unique maximal submodule, and its quotient is the unique (up to isomorphism
) irreducible representation with highest weight
The Verma module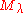
itself is irreducible if and only if none of the coordinates of 
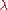in the basis of fundamental weights is from the set 
.
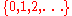The Verma module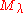
is called regular, if its highest weight λ is on the affine Weyl orbit of a dominant weight 
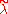. In other word, there exist an element w of the Weyl group W such that
where
is the affine action of the Weyl group.
The Verma module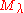
is called singular, if there is no dominant weight on the affine orbit of λ. In this case, there exists a weight 
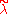so that 
is on the wall of the fundamental Weyl chamber (δ is the sum of all fundamental weights).
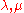a non-trivial homomorphism
may exist only if
and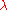 
are linked with an affine action of the Weyl group
of the Lie algebra 
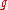. This follows easily from the Harish-Chandra theorem
on infinitesimal central characters.
Each homomorphism of Verma modules is injective and the dimension
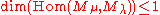
for any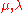
. So, there exists a nonzero 
if and only if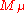 
is isomorphic to a (unique) submodule of 
.
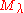The full classification of Verma module homomorphisms was done by Bernstein-Gelfand-Gelfand and Verma and can be summed up in the following statement:
If the Verma modules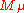
and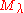 
are regular, then there exists a unique dominant weight 
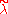and unique elements w, w′ of the Weyl group
W such that
and
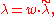
where
is the affine action of the Weyl group. If the weights are further integral, then there exists a nonzero homomorphism
if and only if
in the Bruhat ordering of the Weyl group.
Jordan
Let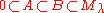
be a sequence of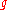
-modules so that the quotient B/A is irreducible with highest weight μ. Then there exists a nonzero homomorphism 
.
An easy consequence of this is, that for any highest weight modules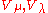
such that
there exists a nonzero homomorphism
.
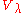be a finite dimensional irreducible representation of the Lie algebra
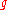with highest weight λ. We know from the section about homomorphisms of Verma modules that there exists a homomorphism
if and only if
in the Bruhat ordering of the Weyl group
. The following theorem describes a resolution
of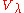
in terms of Verma modules (it was proved by Bernstein
-Gelfand
-Gelfand in 1975) :
A similar resolution exists for generalized Verma module
s as well. It is denoted shortly as the BGG resolution.
Recently, these resolutions were studied in special cases, because of their connections to invariant differential operators in a special type of Cartan geometry, the parabolic geometries. These are Cartan geometries modeled on the pair (G, P) where G is a Lie group
and P a parabolic subgroup)..
Daya-Nand Verma
Daya-Nand Verma is a mathematician retired from the Tata Institute of Fundamental Research. The Verma modules are named after him. He was one of Nathan Jacobson's students at Yale University.-Select publications:...
, are objects in the representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
.
The definition of a Verma module looks complicated, but Verma modules are very natural objects, with useful properties. Their homomorphisms correspond to invariant differential operators over flag manifold
Flag manifold
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
s.
Verma modules can be used to prove that an irreducible highest weight module with highest weight
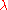is finite dimensionalDimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
, if and only if the weight
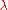is dominant and integral.Definition of Verma modules
The definition relies on a stack of relatively dense notation. Let be a field and denote the following:
-
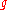, a semisimple Lie algebra over 
, with universal enveloping algebraUniversal enveloping algebraIn mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
. -
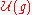, a Borel subalgebra of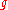 
, with universal enveloping algebra 
. -
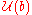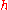, a Cartan subalgebra of 
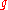. We do not consider its universal enveloping algebra. -
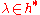, a fixed weightWeight (representation theory)In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
.
To define the Verma module, we begin by defining some other modules:
-
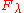, the one-dimensional 
-vector space (i.e. whose underlying set is 
itself) together with a 
-moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
structure such that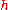
acts as multiplication by 
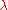and the positive root spacesRoot systemIn mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
act trivially. As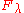
is a left 
-module, it is consequently a left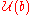 
-module. - Using the Poincaré-Birkhoff-Witt theorem, there is a natural right
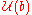-module structure on 
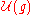by right multiplication of a subalgebra. 
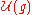is naturally a left 
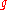-module, and together with this structure, it is a 
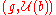-bimoduleBimoduleIn abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
.
Now we can define the Verma module (with respect to
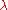) as
which is naturally a left
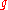-module (i.e. an infinite-dimensional representation of 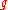). The Poincaré-Birkhoff-Witt theorem implies that the underlying vector space of 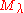is isomorphic to
where
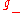is the Lie subalgebra generated by the negative root spaces of 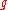.Basic properties
Verma modules, considered as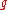-modulesModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, are highest weight modules, i.e. they are generated by a highest weight vector. This highest weight vector is
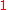(the first is the unit in 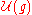and the second isthe unit in the field
, considered as the -moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
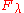) and it has weight 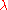.Verma modules are weight modules, i.e.
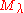is a direct sumDirect sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of all its weight spaces. Each weight space in
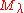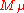is finite dimensional and the dimension of the -weight space is the number of possibilities how to obtain as a sum of positive roots (this is closely related to the so-called Kostant partition functionKostant partition function
In representation theory, the Kostant partition function, introduced by , of a root system \Delta is the number of ways one can represent a vector as an integral non-negative sum of the positive roots \Delta^+\subset\Delta...
).
Verma modules have a very important property: If
is any representation generated by a highest weight vector of weight 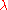, there is a surjective 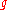-homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
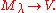That is, all representations with highest weight 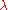that are generated by the highest weight vector (so called highest weight modules) are quotientsQuotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of
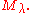
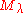contains a unique maximal submodule, and its quotient is the unique (up to isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
) irreducible representation with highest weight
The Verma module
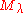itself is irreducible if and only if none of the coordinates of 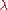in the basis of fundamental weights is from the set 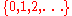.The Verma module
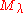is called regular, if its highest weight λ is on the affine Weyl orbit of a dominant weight 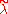. In other word, there exist an element w of the Weyl group W such thatwhere
is the affine action of the Weyl group.The Verma module
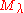is called singular, if there is no dominant weight on the affine orbit of λ. In this case, there exists a weight 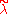so that is on the wall of the fundamental Weyl chamber (δ is the sum of all fundamental weights).Homomorphisms of Verma modules
For any two weights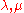 a non-trivial homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
may exist only if
and 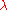are linked with an affine action of the Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of the Lie algebra 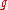. This follows easily from the Harish-Chandra theoremHarish-Chandra theorem
In matheamtics, Harish-Chandra theorem may refer to one of several theorems due to Harish-Chandra,including:*Harish-Chandra's theorem on the Harish-Chandra isomorphism*Harish-Chandra's classification of discrete series representations...
on infinitesimal central characters.
Each homomorphism of Verma modules is injective and the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
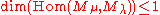
for any
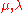. So, there exists a nonzero if and only if 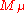is isomorphic to a (unique) submodule of 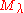.The full classification of Verma module homomorphisms was done by Bernstein-Gelfand-Gelfand and Verma and can be summed up in the following statement:
There exists a nonzero homomorphismif and only if there exists
a sequence of weights
such thatfor some positive roots
(and
is the corresponding root reflection and
is the sum of all fundamental weights) and for each
is a natural number (
is the coroot associated to the root
).
If the Verma modules
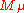and 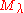are regular, then there exists a unique dominant weight 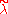and unique elements w, w′ of the Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
W such that
- P
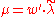
and
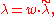
where
is the affine action of the Weyl group. If the weights are further integral, then there exists a nonzero homomorphismif and only if
in the Bruhat ordering of the Weyl group.
JordanCamille JordanMarie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
–HölderOtto HölderOtto Ludwig Hölder was a German mathematician born in Stuttgart.Hölder first studied at the Polytechnikum and then in 1877 went to Berlin where he was a student of Leopold Kronecker, Karl Weierstraß, and Ernst Kummer.He is famous for many things including: Hölder's inequality, the Jordan–Hölder...
series
Let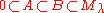be a sequence of
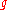-modules so that the quotient B/A is irreducible with highest weight μ. Then there exists a nonzero homomorphism .An easy consequence of this is, that for any highest weight modules
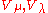such thatthere exists a nonzero homomorphism
.Bernstein–Gelfand–Gelfand resolution
Let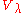 be a finite dimensional irreducible representation of the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
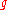with highest weight λ. We know from the section about homomorphisms of Verma modules that there exists a homomorphismif and only if
in the Bruhat ordering of the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
. The following theorem describes a resolution
Resolution (algebra)
In mathematics, particularly in abstract algebra and homological algebra, a resolution is a sequence of objects which is used to describe the structure of a module, or, more generally, the structure of an object in an abelian category.Generally, if the objects involved in the sequence have a...
of
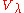in terms of Verma modules (it was proved by BernsteinJoseph Bernstein
Joseph Bernstein is an Israeli mathematician working at Tel Aviv University. He works in algebraic geometry, representation theory, and number theory....
-Gelfand
Israel Gelfand
Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
-Gelfand in 1975) :
There exists an exact sequence of-homomorphisms
where n is the length of the largest element of the Weyl group.
A similar resolution exists for generalized Verma module
Generalized Verma module
In mathematics, generalized Verma modules are a generalization of a Verma module, and are objects in the representation theory of Lie algebras. They were studied originally by James Lepowsky in the nineteen seventies. The motivation for their study is that their homomorphisms correspond to...
s as well. It is denoted shortly as the BGG resolution.
Recently, these resolutions were studied in special cases, because of their connections to invariant differential operators in a special type of Cartan geometry, the parabolic geometries. These are Cartan geometries modeled on the pair (G, P) where G is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and P a parabolic subgroup)..
See also
- Lie algebra representation
- Universal enveloping algebraUniversal enveloping algebraIn mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
- Generalized Verma moduleGeneralized Verma moduleIn mathematics, generalized Verma modules are a generalization of a Verma module, and are objects in the representation theory of Lie algebras. They were studied originally by James Lepowsky in the nineteen seventies. The motivation for their study is that their homomorphisms correspond to...