In topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

, especially algebraic topology

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

, the cone CX of a topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

X is the quotient space

Quotient space

In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...

:


of the product

Product topology

In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...

 of X with the unit interval

Unit interval

In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...

 I = [0, 1].
Intuitively we make X into a cylinder

Cylinder (geometry)

A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...

 and collapse one end of the cylinder to a point.

If X sits inside Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

, the cone on X is homeomorphic to the union

Union (set theory)

In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...

 of lines from X to another point. That is, the topological cone agrees with the geometric cone when defined. However, the topological cone construction is more general.

Examples

• The cone over a point p of the real line is the interval {p} x [0,1].
• The cone over two points {0,1} is a "V" shape with endpoints at {0} and {1}.
• The cone over an interval I of the real line is a filled-in triangle
  Triangle
  A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
  
  , otherwise known as a 2-simplex (see the final example).
• The cone over a polygon
  Polygon
  In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
  
   P is a pyramid with base P.
• The cone over a disk
  Disk (mathematics)
  In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
  
   is the solid cone
  Cone (geometry)
  A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
  
   of classical geometry (hence the concept's name).
• The cone over a circle
  Circle
  A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
  
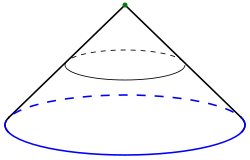
   is the curved surface of the solid cone:

This in turn is homeomorphic to the closed disc.

• In general, the cone over an n-sphere is homeomorphic to the closed (n+1)-ball
  Ball (mathematics)
  In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
  
  .
• The cone over an n-simplex
  Simplex
  In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
  
   is an (n+1)-simplex.

Properties

All cones are path-connected since every point can be connected to the vertex point. Furthermore, every cone is contractible to the vertex point by the homotopy

Homotopy

In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...

h_t(x,s) = (x, (1−t)s).

The cone is used in algebraic topology precisely because it embeds a space as a subspace of a contractible space.

When X is compact

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

 and Hausdorff

Hausdorff space

In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...

 (essentially, when X can be embedded in Euclidean space), then the cone CX can be visualized as the collection of lines joining every point of X to a single point. However, this picture fails when X is not compact or not Hausdorff, as generally the quotient topology on CX will be finer than the set of lines joining X to a point.

Reduced cone

If is a pointed space

Pointed space

In mathematics, a pointed space is a topological space X with a distinguished basepoint x0 in X. Maps of pointed spaces are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f = y0...

, there is a related construction, the reduced cone, given by

With this definition, the natural inclusion becomes a based map, where we take to be the basepoint of the reduced cone.

Cone functor

The map induces a functor

Functor

In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....

  on the category of topological spaces

Category of topological spaces

In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...

 Top.

See also

• Cone (disambiguation)
• Suspension (topology)
• Mapping cone
  Mapping cone
  In mathematics, especially homotopy theory, the mapping cone is a construction C_f of topology, analogous to a quotient space. It is also called the homotopy cofiber, and also notated Cf.-Definition:...
  
  
• Join (topology)
  Join (topology)
  In topology, a field of mathematics, the join of two topological spaces A and B, often denoted by A\star B, is defined to be the quotient space / R, \,...