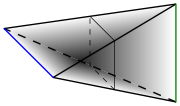
In topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

, a field of mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the join of two topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

s A and B, often denoted by , is defined to be the quotient space

Quotient space

In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...

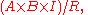
where I is the interval

Interval (mathematics)

In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...

 [0, 1] and R is the relation defined by
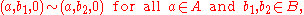
In effect, one is collapsing to and to .

Intuitively, is formed by taking the disjoint union

Disjoint union (topology)

In general topology and related areas of mathematics, the disjoint union of a family of topological spaces is a space formed by equipping the disjoint union of the underlying sets with a natural topology called the disjoint union topology...

 of the two spaces and attaching a line segment joining every point in A to every point in B.

Properties

• The join is homeomorphic to sum of cartesian products of cones over spaces and spaces itself, where sum is taken over cartesian product
  Cartesian product
  In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
  
   of spaces: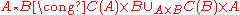

and is homotopy equivalent to suspension of smash product

Smash product

In mathematics, the smash product of two pointed spaces X and Y is the quotient of the product space X × Y under the identifications  ∼  for all x ∈ X and y ∈ Y. The smash product is usually denoted X ∧ Y...

 of spaces:

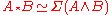
Examples

• The join of A and B, regarded as subsets of n-dimensional Euclidean space is homotopy equivalent to the space of paths in n-dimensional Euclidean space
  Euclidean space
  In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
  
  , beginning in A and ending in B.
• The join of a space X with a one-point space is called the cone
  Cone (topology)
  In topology, especially algebraic topology, the cone CX of a topological space X is the quotient space:CX = /\,of the product of X with the unit interval I = [0, 1]....
  
   CX of X.
• The join of a space X with 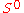(the 0-dimensional sphere
  Sphere
  A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
  
  , or, the discrete space
  Discrete space
  In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
  
   with two points) is called the suspension of X.
• The join of the spheres and 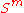is the sphere .