.gif)
Suspension (topology)
Encyclopedia
In topology
, the suspension SX of a topological space
X is the quotient space
:
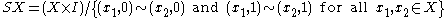
of the product
of X with the unit interval
I = [0, 1]. Intuitively, we make X into a cylinder
and collapse both ends to two points. One views X as "suspended" between the end points. One can also view the suspension as two cones
on X glued together
at their base (or as a quotient of a single cone).
Given a continuous map
there is a map 
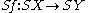defined by 
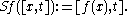This makes 
into a functor
from the category of topological spaces into itself. In rough terms S increases the dimension of a space by one: it takes an n-sphere
to an (n + 1)-sphere for n ≥ 0.
Note that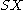
is homeomorphic to the join
where 
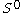is a discrete space
with two points.
The space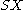
is sometimes called the unreduced, unbased, or free suspension of 
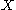, to distinguish it from the reduced suspension described below.
The suspension can be used to construct a homomorphism of homotopy group
s, to which the Freudenthal suspension theorem
applies. In homotopy theory, the phenomena which are preserved under suspension, in a suitable sense, make up stable homotopy theory
.
(with basepoint x0), there is a variation of the suspension which is sometimes more useful. The reduced suspension or based suspension ΣX of X is the quotient space:
.
This is the equivalent to taking SX and collapsing the line (x0 × I) joining the two ends to a single point. The basepoint of ΣX is the equivalence class of (x0, 0).
One can show that the reduced suspension of X is homeomorphic to the smash product
of X with the unit circle
S1.
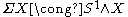
For well-behaved
spaces, such as CW complex
es, the reduced suspension of X is homotopy equivalent to the ordinary suspension.
Σ gives rise to a functor from the category of pointed spaces to itself. An important property of this functor is that it is a left adjoint to the functor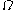
taking a (based) space 
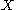to its loop space 
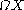. In other words,
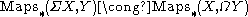
naturally, where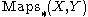
stands for continuous maps which preserve basepoints. This is not the case for unreduced suspension and free loop space.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the suspension SX of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
:
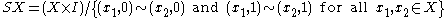
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of X with the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
I = [0, 1]. Intuitively, we make X into a cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
and collapse both ends to two points. One views X as "suspended" between the end points. One can also view the suspension as two cones
Cone (topology)
In topology, especially algebraic topology, the cone CX of a topological space X is the quotient space:CX = /\,of the product of X with the unit interval I = [0, 1]....
on X glued together
Adjunction space
In mathematics, an adjunction space is a common construction in topology where one topological space is attached or "glued" onto another. Specifically, let X and Y be a topological spaces with A a subspace of Y. Let f : A → X be a continuous map...
at their base (or as a quotient of a single cone).
Given a continuous map
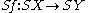there is a map defined by 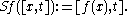This makes into a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the category of topological spaces into itself. In rough terms S increases the dimension of a space by one: it takes an n-sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
to an (n + 1)-sphere for n ≥ 0.
Note that
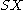is homeomorphic to the joinJoin (topology)
In topology, a field of mathematics, the join of two topological spaces A and B, often denoted by A\star B, is defined to be the quotient space / R, \,...
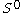where is a discrete spaceDiscrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
with two points.
The space
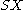is sometimes called the unreduced, unbased, or free suspension of 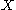, to distinguish it from the reduced suspension described below.The suspension can be used to construct a homomorphism of homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s, to which the Freudenthal suspension theorem
Freudenthal suspension theorem
In mathematics, and specifically in the field of homotopy theory, the Freudenthal suspension theorem is the fundamental result leading to the concept of stabilization of homotopy groups and ultimately to stable homotopy theory. It explains the behavior of simultaneously taking suspensions and...
applies. In homotopy theory, the phenomena which are preserved under suspension, in a suitable sense, make up stable homotopy theory
Stable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
.
Reduced suspension
If X is a pointed spacePointed space
In mathematics, a pointed space is a topological space X with a distinguished basepoint x0 in X. Maps of pointed spaces are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f = y0...
(with basepoint x0), there is a variation of the suspension which is sometimes more useful. The reduced suspension or based suspension ΣX of X is the quotient space:
.This is the equivalent to taking SX and collapsing the line (x0 × I) joining the two ends to a single point. The basepoint of ΣX is the equivalence class of (x0, 0).
One can show that the reduced suspension of X is homeomorphic to the smash product
Smash product
In mathematics, the smash product of two pointed spaces X and Y is the quotient of the product space X × Y under the identifications ∼ for all x ∈ X and y ∈ Y. The smash product is usually denoted X ∧ Y...
of X with the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
S1.
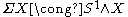
For well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
spaces, such as CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es, the reduced suspension of X is homotopy equivalent to the ordinary suspension.
Σ gives rise to a functor from the category of pointed spaces to itself. An important property of this functor is that it is a left adjoint to the functor
taking a (based) space 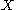to its loop space 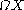. In other words,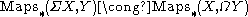naturally, where
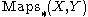stands for continuous maps which preserve basepoints. This is not the case for unreduced suspension and free loop space.