Adjunction space
Encyclopedia
In mathematics
, an adjunction space (or attaching space) is a common construction in topology
where one topological space
is attached or "glued" onto another. Specifically, let X and Y be a topological spaces with A a subspace of Y. Let f : A → X be a continuous map (called the attaching map). One forms the adjunction space X ∪f Y by taking the disjoint union
of X and Y and identifying
x with f(x) for all x in A. Schematically,
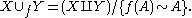
Sometimes, the adjunction is written as
. Intuitively, we think of Y as being glued onto X via the map f.
As a set, X ∪f Y consists of the disjoint union of X and (Y − A). The topology, however, is specified by the quotient construction. In the case where A is a closed
subspace of Y one can show that the map X → X ∪f Y is a closed embedding
and (Y − A) → X ∪f Y is an open embedding.
in the category of topological spaces
. That is to say, the adjunction space is universal
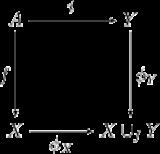
with respect to following commutative diagram
:
Here i is the inclusion map
and φX, φY are the maps obtained by composing the quotient map with the canonical injections into the disjoint union of X and Y. One can form a more general pushout by replacing i with an arbitrary continuous map g — the construction is similar. Conversely, if f is also an inclusion the attaching construction is to simply glue X and Y together along their common subspace.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an adjunction space (or attaching space) is a common construction in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
where one topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is attached or "glued" onto another. Specifically, let X and Y be a topological spaces with A a subspace of Y. Let f : A → X be a continuous map (called the attaching map). One forms the adjunction space X ∪f Y by taking the disjoint union
Disjoint union (topology)
In general topology and related areas of mathematics, the disjoint union of a family of topological spaces is a space formed by equipping the disjoint union of the underlying sets with a natural topology called the disjoint union topology...
of X and Y and identifying
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
x with f(x) for all x in A. Schematically,
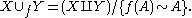
Sometimes, the adjunction is written as
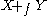. Intuitively, we think of Y as being glued onto X via the map f.As a set, X ∪f Y consists of the disjoint union of X and (Y − A). The topology, however, is specified by the quotient construction. In the case where A is a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
subspace of Y one can show that the map X → X ∪f Y is a closed embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
and (Y − A) → X ∪f Y is an open embedding.
Examples
- A common example of an adjunction space is given when Y is a closed n-ballBall (mathematics)In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
(or cell) and A is the boundary of the ball, the (n−1)-sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
. Inductively attaching cells along their spherical boundaries to this space results in an example of a CW complexCW complexIn topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
. - Adjunction spaces are also used to define connected sumConnected sumIn mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
s of manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s. Here, one first removes open balls from X and Y before attaching the boundaries of the removed balls along an attaching map. - If A is a space with one point then the adjunction is the wedge sumWedge sumIn topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
of X and Y. - If X is a space with one point then the adjunction is the quotient Y/A.
Categorical description
The attaching construction is an example of a pushoutPushout (category theory)
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
in the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
. That is to say, the adjunction space is universal
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
with respect to following commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
Here i is the inclusion map
Inclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
and φX, φY are the maps obtained by composing the quotient map with the canonical injections into the disjoint union of X and Y. One can form a more general pushout by replacing i with an arbitrary continuous map g — the construction is similar. Conversely, if f is also an inclusion the attaching construction is to simply glue X and Y together along their common subspace.