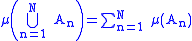Sigma additivity
Encyclopedia
In mathematics
, additivity and sigma additivity of a function
defined on subset
s of a given set are abstractions of the intuitive properties of size
(length
, area
, volume
) of a set.
be a function defined on an algebra of sets 
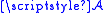with values in [−∞, +∞] (see the extended real number line
). The function
is called additive if, whenever A and B are disjoint sets in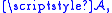 
one has
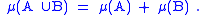
(A consequence of this is that an additive function cannot take both −∞ and +∞ as values, for the expression ∞ − ∞ is undefined.)
One can prove by mathematical induction
that an additive function satisfies
for any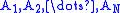
disjoint sets in 
.
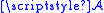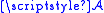is a σ-algebra. If for any sequence
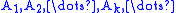of disjoint sets in 
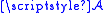one has
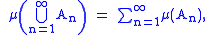
we say that μ is countably additive or σ-additive.
Any σ-additive function is additive but not vice-versa, as shown below.
s, such that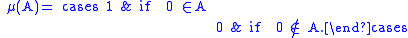
If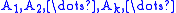
is a sequence of disjoint sets of real numbers, then either none of the sets contains 0, or precisely one of them does. In either case the equality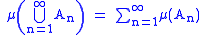
holds.
See measure
and signed measure
for more examples of σ-additive functions.
An example of an additive function which is not σ-additive is obtained by considering μ, defined over the power set of the real number
s by the slightly modified formula
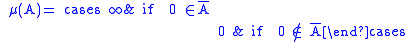
where the bar denotes the closure
of a set.
One can check that this function is additive by using the property that the closure of a finite union of sets is the union of the closures of the sets, and looking at the cases when 0 is in the closure of any of those sets or not. That this function is not σ-additive follows by considering the sequence of disjoint sets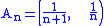
for n=1, 2, 3, ... The union of these sets is the interval (0, 1) whose closure is [0, 1] and μ applied to the union is then infinity, while μ applied to any of the individual sets is zero, so the sum of μ(An) is also zero, which proves the counterexample.
(for example any group
or more commonly a vector space
). For sigma-additivity, one needs in addition that the concept of limit of a sequence
be defined on that set. For example, spectral measures are sigma-additive functions with values in a Banach algebra
. Another example, also from quantum mechanics, is the positive operator-valued measure.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, additivity and sigma additivity of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
defined on subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of a given set are abstractions of the intuitive properties of size
Size
The word size may refer to how big something is. In particular:* Measurement, the process or the result of determining the magnitude of a quantity, such as length or mass, relative to a unit of measurement, such as a meter or a kilogram...
(length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
, area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
, volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
) of a set.
Additive (or finitely additive) set functions
Let be a function defined on an algebra of sets 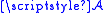with values in [−∞, +∞] (see the extended real number lineExtended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
). The function
is called additive if, whenever A and B are disjoint sets in 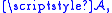one has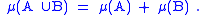(A consequence of this is that an additive function cannot take both −∞ and +∞ as values, for the expression ∞ − ∞ is undefined.)
One can prove by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
that an additive function satisfies
for any
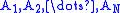disjoint sets in 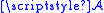.σ-additive set functions
Suppose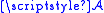 is a σ-algebra. If for any sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
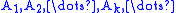of disjoint sets in 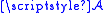one has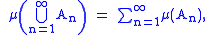we say that μ is countably additive or σ-additive.
Any σ-additive function is additive but not vice-versa, as shown below.
Basic properties
Useful properties of an additive function μ include the following:- μ(∅) = 0.
- If μ is non-negative and A ⊆ B, then μ(A) ≤ μ(B).
- If A ⊆ B, then μ(B - A) = μ(B) - μ(A).
- Given A and B, μ(A ∪ B) + μ(A ∩ B) = μ(A) + μ(B).
Examples
An example of a σ-additive function is the function μ defined over the power set of the real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, such that
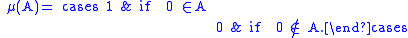
If
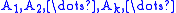is a sequence of disjoint sets of real numbers, then either none of the sets contains 0, or precisely one of them does. In either case the equality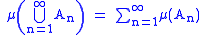holds.
See measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
and signed measure
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
for more examples of σ-additive functions.
An example of an additive function which is not σ-additive is obtained by considering μ, defined over the power set of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s by the slightly modified formula
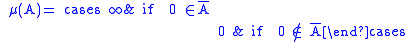
where the bar denotes the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of a set.
One can check that this function is additive by using the property that the closure of a finite union of sets is the union of the closures of the sets, and looking at the cases when 0 is in the closure of any of those sets or not. That this function is not σ-additive follows by considering the sequence of disjoint sets
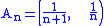
for n=1, 2, 3, ... The union of these sets is the interval (0, 1) whose closure is [0, 1] and μ applied to the union is then infinity, while μ applied to any of the individual sets is zero, so the sum of μ(An) is also zero, which proves the counterexample.
Generalizations
One may define additive functions with values in any additive monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
(for example any group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
or more commonly a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
). For sigma-additivity, one needs in addition that the concept of limit of a sequence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
be defined on that set. For example, spectral measures are sigma-additive functions with values in a Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
. Another example, also from quantum mechanics, is the positive operator-valued measure.
See also
- signed measureSigned measureIn mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
- measure (mathematics)Measure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
- additive functionAdditive functionIn mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
- subadditive functionSubadditive functionIn mathematics, subadditivity is a property of a function that states, roughly, that evaluating the function for the sum of two elements of the domain always returns something less than or equal to the sum of the function's values at each element. There are numerous examples of subadditive...
- Hahn-Kolmogorov theoremHahn-Kolmogorov theoremIn mathematics, the Hahn–Kolmogorov theorem characterizes when a finitely additive function with non-negative values can be extended to a bona fide measure. It is named after the Austrian mathematician Hans Hahn and the Russian/Soviet mathematician Andrey Kolmogorov.-Statement of the theorem:Let ...