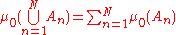Hahn-Kolmogorov theorem
Encyclopedia
In mathematics
, the Hahn–Kolmogorov theorem characterizes when a finitely additive function
with non-negative (possibly infinite) values can be extended to a bona fide measure
. It is named after the Austria
n mathematician
Hans Hahn
and the Russia
n/Soviet mathematician Andrey Kolmogorov
.
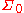 be an algebra of subsets of a set
be an algebra of subsets of a set  Consider a function
Consider a function

which is finitely additive, meaning that
for any positive integer
N and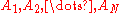 disjoint sets in
disjoint sets in 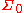 .
.
Assume that this function satisfies the stronger sigma additivity assumption

for any disjoint family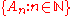 of elements of
of elements of  such that
such that 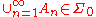 . (Functions
. (Functions 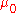 obeying these two properties are known as pre-measures.) Then,
obeying these two properties are known as pre-measures.) Then,
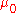 extends to a measure defined on the sigma-algebra
extends to a measure defined on the sigma-algebra
 generated by
generated by 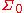 ; i.e., there exists a measure
; i.e., there exists a measure
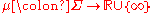
such that its restriction to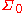 coincides with
coincides with 
If is
is  -finite, then the extension is unique.
-finite, then the extension is unique.
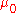 is not
is not  -finite then the extension need not be unique, even if the extension itself is
-finite then the extension need not be unique, even if the extension itself is  -finite.
-finite.
Here is an example:
We call rational closed-open interval, any subset of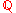 of the form
of the form 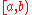 , where
, where  .
.
Let be
be 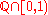 and let
and let 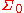 be the algebra of all finite union of rational closed-open intervals contained in
be the algebra of all finite union of rational closed-open intervals contained in 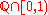 . It is easy to prove that
. It is easy to prove that 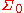 is, in fact, an algebra. It is also easy to see that every non-empty set in
is, in fact, an algebra. It is also easy to see that every non-empty set in  is infinite.
is infinite.
Let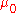 be the counting set function (
be the counting set function ( ) defined in
) defined in 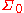 .
.
It is clear that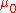 is finitely additive and
is finitely additive and  -additive in
-additive in 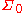 . Since every non-empty set in
. Since every non-empty set in 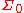 is infinite, we have, for every non-empty set
is infinite, we have, for every non-empty set 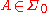 ,
, 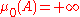
Now, let be the
be the  -algebra generated by
-algebra generated by 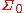 . It is easy to see that
. It is easy to see that  is the Borel
is the Borel  -algebra of subsets of
-algebra of subsets of  , and both
, and both  and
and  are measures defined on
are measures defined on  and both are extensions of
and both are extensions of 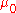 .
.
 from an algebra of sets to a potentially much bigger sigma-algebra, guaranteeing that the extension is unique (if
from an algebra of sets to a potentially much bigger sigma-algebra, guaranteeing that the extension is unique (if 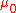 is
is  -finite), and moreover that it does not fail to satisfy the sigma-additivity of the original function.
-finite), and moreover that it does not fail to satisfy the sigma-additivity of the original function.
----
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hahn–Kolmogorov theorem characterizes when a finitely additive function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
with non-negative (possibly infinite) values can be extended to a bona fide measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
. It is named after the Austria
Austria
Austria , officially the Republic of Austria , is a landlocked country of roughly 8.4 million people in Central Europe. It is bordered by the Czech Republic and Germany to the north, Slovakia and Hungary to the east, Slovenia and Italy to the south, and Switzerland and Liechtenstein to the...
n mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Hans Hahn
Hans Hahn
Hans Hahn was an Austrian mathematician who made contributions to functional analysis, topology, set theory, the calculus of variations, real analysis, and order theory.-Biography:...
and the Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n/Soviet mathematician Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
.
Statement of the theorem
Let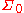 be an algebra of subsets of a set
be an algebra of subsets of a set  Consider a function
Consider a function
which is finitely additive, meaning that
for any positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
N and
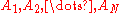 disjoint sets in
disjoint sets in 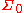 .
.Assume that this function satisfies the stronger sigma additivity assumption

for any disjoint family
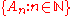 of elements of
of elements of  such that
such that 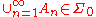 . (Functions
. (Functions 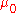 obeying these two properties are known as pre-measures.) Then,
obeying these two properties are known as pre-measures.) Then,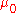 extends to a measure defined on the sigma-algebra
extends to a measure defined on the sigma-algebraSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
 generated by
generated by 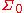 ; i.e., there exists a measure
; i.e., there exists a measure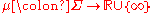
such that its restriction to
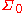 coincides with
coincides with 
If
 is
is  -finite, then the extension is unique.
-finite, then the extension is unique.Non-uniqueness of the extension
If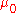 is not
is not  -finite then the extension need not be unique, even if the extension itself is
-finite then the extension need not be unique, even if the extension itself is  -finite.
-finite.Here is an example:
We call rational closed-open interval, any subset of
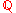 of the form
of the form 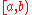 , where
, where  .
.Let
 be
be 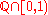 and let
and let 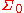 be the algebra of all finite union of rational closed-open intervals contained in
be the algebra of all finite union of rational closed-open intervals contained in 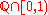 . It is easy to prove that
. It is easy to prove that 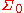 is, in fact, an algebra. It is also easy to see that every non-empty set in
is, in fact, an algebra. It is also easy to see that every non-empty set in  is infinite.
is infinite.Let
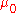 be the counting set function (
be the counting set function ( ) defined in
) defined in 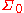 .
.It is clear that
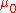 is finitely additive and
is finitely additive and  -additive in
-additive in 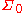 . Since every non-empty set in
. Since every non-empty set in 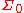 is infinite, we have, for every non-empty set
is infinite, we have, for every non-empty set 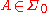 ,
, 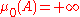
Now, let
 be the
be the  -algebra generated by
-algebra generated by 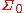 . It is easy to see that
. It is easy to see that  is the Borel
is the Borel  -algebra of subsets of
-algebra of subsets of  , and both
, and both  and
and  are measures defined on
are measures defined on  and both are extensions of
and both are extensions of 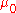 .
.Comments
This theorem is remarkable for it allows one to construct a measure by first defining it on a small algebra of sets, where its sigma additivity could be easy to verify, and then this theorem guarantees its extension to a sigma-algebra. The proof of this theorem is not trivial, since it requires extending from an algebra of sets to a potentially much bigger sigma-algebra, guaranteeing that the extension is unique (if
from an algebra of sets to a potentially much bigger sigma-algebra, guaranteeing that the extension is unique (if 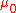 is
is  -finite), and moreover that it does not fail to satisfy the sigma-additivity of the original function.
-finite), and moreover that it does not fail to satisfy the sigma-additivity of the original function.See also
- Carathéodory's extension theoremCarathéodory's extension theoremIn measure theory, Carathéodory's extension theorem states that any σ-finite measure defined on a given ring R of subsets of a given set Ω can be uniquely extended to the σ-algebra generated by R...
- pre-measurePre-measureIn mathematics, a pre-measure is a function that is, in some sense, a precursor to a bona fide measure on a given space. Pre-measures are particularly useful in fractal geometry and dimension theory, where they can be used to define measures such as Hausdorff measure and packing measure on metric...
----