Hahn decomposition theorem
Encyclopedia
In mathematics
, the Hahn decomposition theorem, named after the Austria
n mathematician
Hans Hahn
, states that given a measurable space
(X,Σ) and a signed measure
μ defined on the σ-algebra Σ, there exist two sets P and N in Σ such that:
Moreover, this decomposition is essentially unique, in the sense that for any other pair (P' , N' ) of measurable sets fulfilling the above three conditions, the symmetric difference
s P Δ P' and N Δ N' are μ-null set
s in the strong sense that every measurable subset of them has zero measure. The pair (P,N) is called a Hahn decomposition of the signed measure μ.
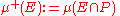
and
for every E in Σ, and it is an easy task to verify that both μ+ and μ– are positive measures on the space (X,Σ), at least one of them is finite (since μ cannot take both +∞ and −∞ as values), and satisfy μ = μ+ − μ–. The pair (μ+, μ–) is called a Jordan decomposition (or sometimes Hahn–Jordan decomposition) of μ.
Claim: Suppose that a set D in Σ satisfies μ(D) ≤ 0. Then there is a negative set A ⊆ D such that μ(A) ≤ μ(D).
Proof of the claim: Define A0 = D. Inductively
assume for a natural number n that An ⊆ D has been constructed. Let
denote the supremum
of μ(B) for all the measurable subsets B of An. This supremum might a priori be infinite. Since the empty set ∅ is a possible B in the definition of tn and μ(∅) = 0, we have tn ≥ 0. By definition of tn there exists a Bn ⊆ An in Σ satisfying
Set An+1 = An \ Bn to finish the induction step. Define
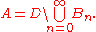
Since the sets (Bn)n≥0 are disjoint subsets of D, it follows from the sigma additivity
of the signed measure μ that
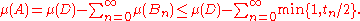
This shows that μ(A) ≤ μ(D). Assume A were not a negative set. That means there exists a B in Σ which is a subset of A and satisfies μ(B) > 0. Then tn ≥ μ(B) for every n, hence the series
on the right has to diverge to +∞, which means μ(A) = –∞, which is not allowed. Therefore, A must be a negative set.
Construction of the decomposition: Set N0 = ∅. Inductively, given Nn, define
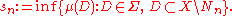
as the infimum
of μ(D) for all the measurable subsets D of X \ Nn. This infimum might a priori be –∞.
Since the empty set is a possible D and μ(∅) = 0, we have sn ≤ 0. Hence there exists a Dn in Σ with Dn ⊆ X \ Nn and
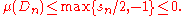
By the claim above, there is a negative set An ⊆ Dn such that μ(An) ≤ μ(Dn). Define Nn+1 = Nn ∪ An
to finish the induction step.
Define
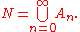
Since the sets (An)n≥0 are disjoint, we have for every B ⊆ N in Σ that
by the sigma additivity of μ. In particular, this shows that N is a negative set. Define P = X \ N. If P were not a positive set, there exists a D ⊆ P in Σ with μ(D) < 0. Then sn ≤ μ(D) for all n and
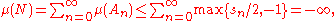
which is not allowed for μ. Therefore, P is a positive set.
Proof of the uniqueness statement:
Suppose that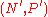
is another Hahn decomposition of 
. Then 
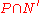is a positive set and also a negative set. Therefore, every measurable subset of it has measure zero. The same applies to 
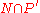. Since
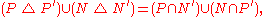
this completes the proof. Q.E.D.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hahn decomposition theorem, named after the Austria
Austria
Austria , officially the Republic of Austria , is a landlocked country of roughly 8.4 million people in Central Europe. It is bordered by the Czech Republic and Germany to the north, Slovakia and Hungary to the east, Slovenia and Italy to the south, and Switzerland and Liechtenstein to the...
n mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Hans Hahn
Hans Hahn
Hans Hahn was an Austrian mathematician who made contributions to functional analysis, topology, set theory, the calculus of variations, real analysis, and order theory.-Biography:...
, states that given a measurable space
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
(X,Σ) and a signed measure
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
μ defined on the σ-algebra Σ, there exist two sets P and N in Σ such that:
- P ∪ N = X and P ∩ N = ∅.
- For each E in Σ such that E ⊆ P one has μ(E) ≥ 0; that is, P is a positive setPositive and negative setsIn measure theory, given a measurable space and a signed measure μ on it, a set A ∈ Σ is called a positive set for μ if every Σ-measurable subset of A has nonnegative measure; that is, for every E ⊆ A that satisfies E ∈ Σ, one has μ ≥ 0.Similarly, a set A ∈ Σ is called a negative set for μ if for...
for μ. - For each E in Σ such that E ⊆ N one has μ(E) ≤ 0; that is, N is a negative set for μ.
Moreover, this decomposition is essentially unique, in the sense that for any other pair (P
Symmetric difference
In mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
s P Δ P
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
s in the strong sense that every measurable subset of them has zero measure. The pair (P,N) is called a Hahn decomposition of the signed measure μ.
Hahn–Jordan decomposition
A consequence of this theorem is the Jordan decomposition theorem, which states that every signed measure μ can be expressed as a difference of two positive measures μ+ and μ–, at least one of which is finite; μ+ and μ– are called the positive and negative part of μ, respectively. The two measures can be defined as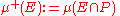and
for every E in Σ, and it is an easy task to verify that both μ+ and μ– are positive measures on the space (X,Σ), at least one of them is finite (since μ cannot take both +∞ and −∞ as values), and satisfy μ = μ+ − μ–. The pair (μ+, μ–) is called a Jordan decomposition (or sometimes Hahn–Jordan decomposition) of μ.
Proof of the Hahn decomposition theorem
Preparation: Assume that μ does not take the value −∞ (otherwise decompose according to −μ). As mentioned above, a negative set is a set A in Σ such that μ(B) ≤ 0 for every B in Σ which is a subset of A.Claim: Suppose that a set D in Σ satisfies μ(D) ≤ 0. Then there is a negative set A ⊆ D such that μ(A) ≤ μ(D).
Proof of the claim: Define A0 = D. Inductively
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
assume for a natural number n that An ⊆ D has been constructed. Let
denote the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of μ(B) for all the measurable subsets B of An. This supremum might a priori be infinite. Since the empty set ∅ is a possible B in the definition of tn and μ(∅) = 0, we have tn ≥ 0. By definition of tn there exists a Bn ⊆ An in Σ satisfying
Set An+1 = An \ Bn to finish the induction step. Define
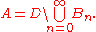
Since the sets (Bn)n≥0 are disjoint subsets of D, it follows from the sigma additivity
Sigma additivity
In mathematics, additivity and sigma additivity of a function defined on subsets of a given set are abstractions of the intuitive properties of size of a set.- Additive set functions :...
of the signed measure μ that
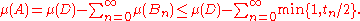
This shows that μ(A) ≤ μ(D). Assume A were not a negative set. That means there exists a B in Σ which is a subset of A and satisfies μ(B) > 0. Then tn ≥ μ(B) for every n, hence the series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
on the right has to diverge to +∞, which means μ(A) = –∞, which is not allowed. Therefore, A must be a negative set.
Construction of the decomposition: Set N0 = ∅. Inductively, given Nn, define
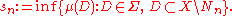
as the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of μ(D) for all the measurable subsets D of X \ Nn. This infimum might a priori be –∞.
Since the empty set is a possible D and μ(∅) = 0, we have sn ≤ 0. Hence there exists a Dn in Σ with Dn ⊆ X \ Nn and
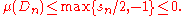
By the claim above, there is a negative set An ⊆ Dn such that μ(An) ≤ μ(Dn). Define Nn+1 = Nn ∪ An
to finish the induction step.
Define
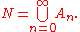
Since the sets (An)n≥0 are disjoint, we have for every B ⊆ N in Σ that
by the sigma additivity of μ. In particular, this shows that N is a negative set. Define P = X \ N. If P were not a positive set, there exists a D ⊆ P in Σ with μ(D) < 0. Then sn ≤ μ(D) for all n and
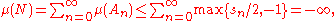
which is not allowed for μ. Therefore, P is a positive set.
Proof of the uniqueness statement:
Suppose that
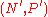is another Hahn decomposition of . Then 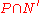is a positive set and also a negative set. Therefore, every measurable subset of it has measure zero. The same applies to 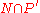. Since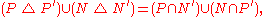this completes the proof. Q.E.D.
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
External links
- Hahn decomposition theorem at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
.