
Geometric measure theory
Encyclopedia
In mathematics
, geometric measure theory (GMT) is the study of the geometric
properties of the measures
of sets (typically in Euclidean space
s), including such things as arc length
s and area
s. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable set
s. It has applications in various areas, including image processing
and fracture mechanics
.
Deep results in geometric measure theory identified a dichotomy between rectifiable sets on the one hand and purely unrectifiable or fractal
sets on the other. The Compactness Theorem for rectifiable sets, together with deep regularity results, solves for example the Plateau problem
—proves that every smooth closed curve in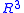 bounds a smooth "soap film" or minimal surface, defined as a surface with mean curvature 0. (The earlier result of Jesse Douglas
bounds a smooth "soap film" or minimal surface, defined as a surface with mean curvature 0. (The earlier result of Jesse Douglas
which won him the first Fields Medal
in 1936 allowed nonphysical self-intersections.) Later Jean Taylor http://www.math.rutgers.edu/~taylor/ after Fred Almgren
proved Plateau's laws
for the kind of singularities that can occur in more general soap films and soap bubbles clusters.
Some basic results in geometric measure theory can turn out to have surprisingly far-reaching consequences. For example, the Brunn-Minkowski inequality for the n-dimensional volumes of convex bodies
K and L,
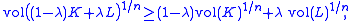
can be proved on a single page, yet quickly yields the classical isoperimetric inequality. The Brunn-Minkowski inequality also leads to Anderson's theorem
in statistics. The proof of the Brunn-Minkowski inequality predates modern measure theory; the development of measure theory and Lebesgue integration
allowed connections to be made between geometry and analysis, to the extent that in an integral form of the Brunn-Minkowski inequality known as the Prékopa–Leindler inequality the geometry seems almost entirely absent.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, geometric measure theory (GMT) is the study of the geometric
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
properties of the measures
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
of sets (typically in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s), including such things as arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
s and area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
s. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable set
Rectifiable set
In mathematics, a rectifiable set is a set that is smooth in a certain measure-theoretic sense. It is an extension of the idea of a rectifiable curve to higher dimensions; loosely speaking, a rectifiable set is a rigorous formulation of a piece-wise smooth set...
s. It has applications in various areas, including image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
and fracture mechanics
Fracture mechanics
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.In...
.
Deep results in geometric measure theory identified a dichotomy between rectifiable sets on the one hand and purely unrectifiable or fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
sets on the other. The Compactness Theorem for rectifiable sets, together with deep regularity results, solves for example the Plateau problem
Plateau's problem
In mathematics, Plateau's problem is to show the existence of a minimal surface with a given boundary, a problem raised by Joseph-Louis Lagrange in 1760. However, it is named after Joseph Plateau who was interested in soap films. The problem is considered part of the calculus of variations...
—proves that every smooth closed curve in
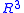 bounds a smooth "soap film" or minimal surface, defined as a surface with mean curvature 0. (The earlier result of Jesse Douglas
bounds a smooth "soap film" or minimal surface, defined as a surface with mean curvature 0. (The earlier result of Jesse DouglasJesse Douglas
Jesse Douglas was an American mathematician. He was born in New York and attended Columbia College of Columbia University from 1920–1924. Douglas was one of two winners of the first Fields Medals, awarded in 1936. He was honored for solving, in 1930, the problem of Plateau, which asks whether a...
which won him the first Fields Medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
in 1936 allowed nonphysical self-intersections.) Later Jean Taylor http://www.math.rutgers.edu/~taylor/ after Fred Almgren
Frederick J. Almgren, Jr.
Frederick Justin Almgren, Jr. was a mathematician working in geometric measure theory...
proved Plateau's laws
Plateau's laws
Plateau's laws describe the structure of soap films. These laws were formulated in the 19th century by the Belgian physicist Joseph Plateau from his experimental observations.Plateau's laws state:# Soap films are made of entire smooth surfaces....
for the kind of singularities that can occur in more general soap films and soap bubbles clusters.
Some basic results in geometric measure theory can turn out to have surprisingly far-reaching consequences. For example, the Brunn-Minkowski inequality for the n-dimensional volumes of convex bodies
Convex body
In mathematics, a convex body in n-dimensional Euclidean space Rn is a compact convex set with non-empty interior.A convex body K is called symmetric if it is centrally symmetric with respect to the origin, i.e. a point x lies in K if and only if its antipode, −x, also lies in K...
K and L,
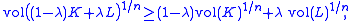
can be proved on a single page, yet quickly yields the classical isoperimetric inequality. The Brunn-Minkowski inequality also leads to Anderson's theorem
Anderson's theorem
In mathematics, Anderson's theorem is a result in real analysis and geometry which says that the integral of an integrable, symmetric, unimodal, non-negative function f over an n-dimensional convex body K does not decrease if K is translated inwards towards the origin...
in statistics. The proof of the Brunn-Minkowski inequality predates modern measure theory; the development of measure theory and Lebesgue integration
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
allowed connections to be made between geometry and analysis, to the extent that in an integral form of the Brunn-Minkowski inequality known as the Prékopa–Leindler inequality the geometry seems almost entirely absent.
See also
- Caccioppoli setCaccioppoli setIn mathematics, a Caccioppoli set is a set whose boundary is measurable and has a finite measure. A synonym is set of finite perimeter...
- Coarea formulaCoarea formulaIn the mathematical field of geometric measure theory, the coarea formula expresses the integral of a function over an open set in Euclidean space in terms of the integral of the level sets of another function...
- Herbert FedererHerbert FedererHerbert Federer was an American mathematician. He is one of the creators of geometric measure theory, at the meeting point of differential geometry and mathematical analysis.-Career:...
- Osgood curveOsgood curveIn mathematics, an Osgood curve is a Jordan curve of positive area. The first example was found by .Examples of Osgood curves can be produced by slightly modifying one of the constructions of space-filling curves with image the unit square to make it an embedding, though the cost is that it no...
- VarifoldVarifoldIn mathematics, a varifold is, loosely speaking, a measure-theoretic generalization of the concept of a differentiable manifold, by replacing differentiability requirements with those provided by rectifiable sets, while maintaining the general algebraic structure usually seen in differential...
External links
- Peter Mörters' GMT page http://www.mathematik.uni-kl.de/~peter/gmt.html
- Toby O'Neil's GMT page with references http://mcs.open.ac.uk/tcon2/gmt.htm

