
Symplectic vector space
Encyclopedia
In mathematics
, a symplectic vector space is a vector space
V (over a field
, for example the real numbers R) equipped with a bilinear form ω : V × V → R that is
The bilinear form ω is said to be a symplectic form in this case.
In practice, the above three properties (skew-symmetric, isotropic and nondegenerate) need not all be checked to see that some bilinear form is symplectic:
Working in a fixed basis
, ω can be represented by a matrix
. The three conditions above say that this matrix must be skew-symmetric
and nonsingular. This is not the same thing as a symplectic matrix, which represents a symplectic transformation of the space.
If V is finite-dimensional then its dimension must necessarily be even since every skew-symmetric matrix of odd size has determinant
zero.
A symplectic form behaves quite differently from a symmetric form, such as the dot product on Euclidean vector spaces. With a Euclidean inner product g, we have g(v,v) > 0 for all nonzero vectors v.
. Typically ω is chosen to be the block matrix

where In is the n × n identity matrix
. In terms of basis vectors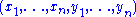 :
:

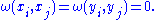
A modified version of the Gram-Schmidt process shows that any finite-dimensional symplectic vector space has a basis such that takes this form, often called a Darboux basis.
takes this form, often called a Darboux basis.
There is another way to interpret this standard symplectic form. Since the model space Rn used above carries much canonical structure which might easily lead to misinterpretation, we will use "anonymous" vector spaces instead.
Let V be a real vector space of dimension n and V∗ its dual space
. Now consider the direct sum W := V ⊕ V∗ of these spaces equipped with the following form:
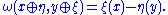
Now choose any basis
(v1, ..., vn) of V and consider its dual basis

We can interpret the basis vectors as lying in W if we write
xi = (vi, 0) and yi = (0, vi∗). Taken together, these form a complete basis of W,
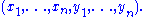
The form defined here can be shown to have the same properties as in the beginning of this section; in other words, every symplectic structure is isomorphic to one of the form V ⊕ V∗.
defined here can be shown to have the same properties as in the beginning of this section; in other words, every symplectic structure is isomorphic to one of the form V ⊕ V∗.
The subspace V is not unique, and a choice of subspace V is called a polarization. The subspaces that give such an isomorphism are called Lagrangian subspaces or simply Lagrangians.
Explicitly, given a Lagrangian subspace (as defined below), then a choice of basis defines a dual basis for a complement, by
defines a dual basis for a complement, by 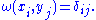
on a vector space is isomorphic to one of the form V ⊕ V.
Using these structures, the tangent bundle
of an n-manifold, considered as a 2n-manifold, has an almost complex structure, and the cotangent bundle
of an n-manifold, considered as a 2n-manifold, has a symplectic structure: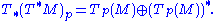
The complex analog to a Lagrangian subspace is a real subspace, a subspace whose complexification is the whole space: W = V ⊕ J'V.
. A volume form on a n-dimensional vector space V is a non-zero multiple of the n-form e1∗ ∧ ... ∧ en∗ where e1, e2, ..., en is a basis of V.
For the standard basis defined in the previous section, we have
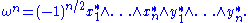
By reordering, one can write
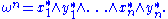
Authors variously define ωn or (−1)n/2ωn as the standard volume form. An occasional factor of n! may also appear, depending on whether the definition of the alternating product contains a factor of n! or not. The volume form defines an orientation
on the symplectic vector space (V, ω).
s.
ƒ preserves the symplectic form. The set of all symplectic transformations forms a group
and in particular a Lie group
, called the symplectic group
and denoted by Sp(V) or sometimes Sp(V,ω). In matrix form symplectic transformations are given by symplectic matrices.
of V. Define the symplectic complement of W to be the subspace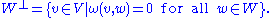
The symplectic complement satisfies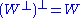
and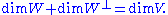
However, unlike orthogonal complements, W⊥ ∩ W need not be 0. We distinguish four cases:
Referring to the canonical vector space R2n above,
A vector space can be thought of as a commutative Lie group (under addition), or equivalently as a commutative Lie algebra, meaning with trivial Lie bracket. The Heisenberg group is a central extension of such a commutative Lie group/algebra: the symplectic form defines the commutation, analogously to the canonical commutation relation
s (CCR), and a Darboux basis corresponds to canonical coordinates – in physics terms, to momentum operator
s and position operator
s.
Indeed, by the Stone–von Neumann theorem
, every representation satisfying the CCR (every representation of the Heisenberg group) is of this form, or more properly unitarily conjugate to the standard one.
Further, the group algebra
of (the dual to) a vector space is the symmetric algebra
, and the group algebra of the Heisenberg group (of the dual) is the Weyl algebra: one can think of the central extension as corresponding to quantization or deformation.
Formally, the symmetric algebra of V is the group algebra of the dual, and the Weyl algebra is the group algebra of the (dual) Heisenberg group
and the Weyl algebra is the group algebra of the (dual) Heisenberg group 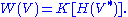 Since passing to group algebras is a contravariant functor, the central extension map
Since passing to group algebras is a contravariant functor, the central extension map 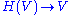 becomes an inclusion
becomes an inclusion 
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a symplectic vector space is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V (over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, for example the real numbers R) equipped with a bilinear form ω : V × V → R that is
- Skew-symmetric: ω(u, v) = −ω(v, u) for all u, v ∈ V.
- Totally isotropicIsotropic quadratic formIn mathematics, a quadratic form over a field F is said to be isotropic if there is a non-zero vector on which it evaluates to zero. Otherwise the quadratic form is anisotropic. More precisely, if q is a quadratic form on a vector space V over F, then a non-zero vector v in V is said to be...
ω(v, v) = 0 for all v ∈ V. - Nondegenerate: if ω(u, v) = 0 for all v ∈ V then u = 0.
The bilinear form ω is said to be a symplectic form in this case.
In practice, the above three properties (skew-symmetric, isotropic and nondegenerate) need not all be checked to see that some bilinear form is symplectic:
- The skew-symmetric property is redundant (as a condition), as it follows from the isotropic property (applied to v, to w and to v+w and then combined). Hence, the skew-symmetric property needs not be checked if the isotropic property is known to hold.
- If the underlying fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
has characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
≠2, the isotropic property is actually equivalent to the skew-symmetric property. Thus, the isotropic property needs not be checked if the skew-symmetric property is known to hold and the field has characteristic ≠2. On the other hand, if the characteristic is 2, the skew-symmetric property is implied by, but does not imply, the isotropic property. In this case every symplectic form is a symmetric form, but not vice versa.
Working in a fixed basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, ω can be represented by a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. The three conditions above say that this matrix must be skew-symmetric
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
and nonsingular. This is not the same thing as a symplectic matrix, which represents a symplectic transformation of the space.
If V is finite-dimensional then its dimension must necessarily be even since every skew-symmetric matrix of odd size has determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
zero.
A symplectic form behaves quite differently from a symmetric form, such as the dot product on Euclidean vector spaces. With a Euclidean inner product g, we have g(v,v) > 0 for all nonzero vectors v.
Standard symplectic space
The standard symplectic space is R2n with the symplectic form given by a nonsingular, skew-symmetric matrixSkew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
. Typically ω is chosen to be the block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...

where In is the n × n identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. In terms of basis vectors
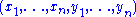 :
:
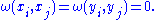
A modified version of the Gram-Schmidt process shows that any finite-dimensional symplectic vector space has a basis such that
 takes this form, often called a Darboux basis.
takes this form, often called a Darboux basis.There is another way to interpret this standard symplectic form. Since the model space Rn used above carries much canonical structure which might easily lead to misinterpretation, we will use "anonymous" vector spaces instead.
Let V be a real vector space of dimension n and V∗ its dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
. Now consider the direct sum W := V ⊕ V∗ of these spaces equipped with the following form:
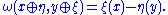
Now choose any basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
(v1, ..., vn) of V and consider its dual basis
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...

We can interpret the basis vectors as lying in W if we write
xi = (vi, 0) and yi = (0, vi∗). Taken together, these form a complete basis of W,
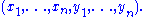
The form
 defined here can be shown to have the same properties as in the beginning of this section; in other words, every symplectic structure is isomorphic to one of the form V ⊕ V∗.
defined here can be shown to have the same properties as in the beginning of this section; in other words, every symplectic structure is isomorphic to one of the form V ⊕ V∗.The subspace V is not unique, and a choice of subspace V is called a polarization. The subspaces that give such an isomorphism are called Lagrangian subspaces or simply Lagrangians.
Explicitly, given a Lagrangian subspace (as defined below), then a choice of basis
 defines a dual basis for a complement, by
defines a dual basis for a complement, by 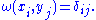
Analogy with complex structures
Just as every symplectic structure is isomorphic to one of the form V ⊕ V∗, every complex structureLinear complex structure
In mathematics, a complex structure on a real vector space V is an automorphism of V that squares to the minus identity, −I. Such a structure on V allows one to define multiplication by complex scalars in a canonical fashion so as to regard V as a complex vector space.Complex structures have...
on a vector space is isomorphic to one of the form V ⊕ V.
Using these structures, the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of an n-manifold, considered as a 2n-manifold, has an almost complex structure, and the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of an n-manifold, considered as a 2n-manifold, has a symplectic structure:
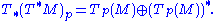
The complex analog to a Lagrangian subspace is a real subspace, a subspace whose complexification is the whole space: W = V ⊕ J'V.
Volume form
Let ω be a form on a n-dimensional real vector space V, ω ∈ Λ2(V). Then ω is non-degenerate if and only if n is even, and ωn/2 = ω ∧ ... ∧ ω is a volume formVolume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
. A volume form on a n-dimensional vector space V is a non-zero multiple of the n-form e1∗ ∧ ... ∧ en∗ where e1, e2, ..., en is a basis of V.
For the standard basis defined in the previous section, we have
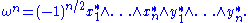
By reordering, one can write
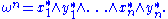
Authors variously define ωn or (−1)n/2ωn as the standard volume form. An occasional factor of n! may also appear, depending on whether the definition of the alternating product contains a factor of n! or not. The volume form defines an orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
on the symplectic vector space (V, ω).
Symplectic map
Suppose that (V,ω) and (W,ρ) are symplectic vector spaces. Then a linear map is called a symplectic map if the pullback preserves the symplectic form, i.e. , where the pullback form is defined by where is the differential of ƒ. Note that symplectic maps are volume-preserving, orientation-preserving, and are vector space isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s.
Symplectic group
If V = W, then a symplectic map is called a linear symplectic transformation of V. In particular, in this case one has that and so the linear transformationLinear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
ƒ preserves the symplectic form. The set of all symplectic transformations forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and in particular a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, called the symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
and denoted by Sp(V) or sometimes Sp(V,ω). In matrix form symplectic transformations are given by symplectic matrices.
Subspaces
Let W be a linear subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of V. Define the symplectic complement of W to be the subspace
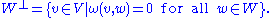
The symplectic complement satisfies
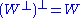
and
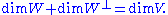
However, unlike orthogonal complements, W⊥ ∩ W need not be 0. We distinguish four cases:
- W is symplectic if W⊥ ∩ W = {0}. This is true if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
ω restricts to a nondegenerate form on W. A symplectic subspace with the restricted form is a symplectic vector space in its own right. - W is isotropic if W ⊆ W⊥. This is true if and only if ω restricts to 0 on W. Any one-dimensional subspace is isotropic.
- W is coisotropic if W⊥ ⊆ W. W is coisotropic if and only if ω descends to a nondegenerate form on the quotient spaceQuotient space (linear algebra)In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
W/W⊥. Equivalently W is coisotropic if and only if W⊥ is isotropic. Any codimensionCodimensionIn mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
-one subspace is coisotropic. - W is Lagrangian if W = W⊥. A subspace is Lagrangian if and only if it is both isotropic and coisotropic. In a finite-dimensional vector space, a Lagrangian subspace is an isotropic one whose dimension is half that of V. Every isotropic subspace can be extended to a Lagrangian one.
Referring to the canonical vector space R2n above,
- the subspace spanned by {x1, y1} is symplectic
- the subspace spanned by {x1, x2} is isotropic
- the subspace spanned by {x1, x2, ..., xn, y1} is coisotropic
- the subspace spanned by {x1, x2, ..., xn} is Lagrangian.
Heisenberg group
A Heisenberg group can be defined for any symplectic vector space, and this is the general way that Heisenberg groups arise.A vector space can be thought of as a commutative Lie group (under addition), or equivalently as a commutative Lie algebra, meaning with trivial Lie bracket. The Heisenberg group is a central extension of such a commutative Lie group/algebra: the symplectic form defines the commutation, analogously to the canonical commutation relation
Canonical commutation relation
In physics, the canonical commutation relation is the relation between canonical conjugate quantities , for example:[x,p_x] = i\hbar...
s (CCR), and a Darboux basis corresponds to canonical coordinates – in physics terms, to momentum operator
Momentum operator
In quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once...
s and position operator
Position operator
In quantum mechanics, the position operator is the operator that corresponds to the position observable of a particle. Consider, for example, the case of a spinless particle moving on a line. The state space for such a particle is L2, the Hilbert space of complex-valued and square-integrable ...
s.
Indeed, by the Stone–von Neumann theorem
Stone–von Neumann theorem
In mathematics and in theoretical physics, the Stone–von Neumann theorem is any one of a number of different formulations of the uniqueness of the canonical commutation relations between position and momentum operators...
, every representation satisfying the CCR (every representation of the Heisenberg group) is of this form, or more properly unitarily conjugate to the standard one.
Further, the group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
of (the dual to) a vector space is the symmetric algebra
Symmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
, and the group algebra of the Heisenberg group (of the dual) is the Weyl algebra: one can think of the central extension as corresponding to quantization or deformation.
Formally, the symmetric algebra of V is the group algebra of the dual,
 and the Weyl algebra is the group algebra of the (dual) Heisenberg group
and the Weyl algebra is the group algebra of the (dual) Heisenberg group 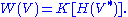 Since passing to group algebras is a contravariant functor, the central extension map
Since passing to group algebras is a contravariant functor, the central extension map 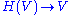 becomes an inclusion
becomes an inclusion 
See also
- A symplectic manifoldSymplectic manifoldIn mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
is a smooth manifold with a smoothly-varying closed symplectic form on each tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other.... - Maslov index
- A symplectic representationSymplectic representationIn mathematical field of representation theory, a quaternionic representation is a representation on a complex vector space V with an invariant quaternionic structure, i.e., an antilinear equivariant mapj\colon V\to V\,which satisfiesj^2=-1.\,...
is a group representationGroup representationIn the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
where each group element acts as a symplectic transformation.

