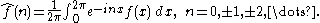Hausdorff–Young inequality
Encyclopedia
In mathematics, the Hausdorff−Young inequality bounds the Lq-norm of the Fourier coefficients of a periodic function
for q ≥ 2. proved the inequality for some special values of q, and proved it in general. More generally the inequality also applies to the Fourier transform
of a function on a locally compact group
, such as Rn, and in this case and gave a sharper form of it called the Babenko–Beckner inequality
.
We consider the Fourier operator
, namely let T be the operator that takes a function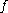
on the unit circle
and outputs
the sequence of its Fourier coefficients
Parseval's theorem
shows that T is bounded from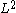
to 
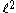with norm 1. On the other hand, clearly,
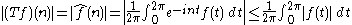
so T is bounded from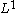
to 
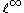with norm 1. Therefore we may invoke the Riesz–Thorin theorem to get, for any 1 < p < 2 that T, as an operator from 
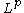to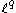 
, is bounded with norm 1, where
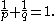
In a short formula, this says that
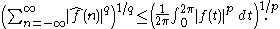
This is the well known Hausdorff–Young inequality. For p > 2 the natural extrapolation of this inequality fails, and the fact that a function belongs to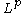
, does not give any additional information on the order of growth of its Fourier series beyond the fact that it is in 
.
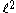. If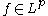
for 
, the optimal bound is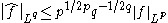
where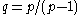
is the Hölder conjugate of 
.
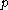Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
for q ≥ 2. proved the inequality for some special values of q, and proved it in general. More generally the inequality also applies to the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of a function on a locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
, such as Rn, and in this case and gave a sharper form of it called the Babenko–Beckner inequality
Babenko–Beckner inequality
In mathematics, the Babenko–Beckner inequality is a sharpened form of the Hausdorff–Young inequality having applications to uncertainty principles in the Fourier analysis of Lp spaces...
.
We consider the Fourier operator
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, namely let T be the operator that takes a function
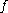on the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
and outputs
the sequence of its Fourier coefficients
Parseval's theorem
Parseval's theorem
In mathematics, Parseval's theorem usually refers to the result that the Fourier transform is unitary; loosely, that the sum of the square of a function is equal to the sum of the square of its transform. It originates from a 1799 theorem about series by Marc-Antoine Parseval, which was later...
shows that T is bounded from
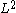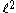to with norm 1. On the other hand, clearly,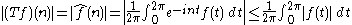so T is bounded from
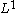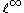to with norm 1. Therefore we may invoke the Riesz–Thorin theorem to get, for any 1 < p < 2 that T, as an operator from 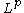to 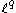, is bounded with norm 1, where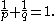In a short formula, this says that
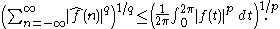
This is the well known Hausdorff–Young inequality. For p > 2 the natural extrapolation of this inequality fails, and the fact that a function belongs to
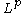, does not give any additional information on the order of growth of its Fourier series beyond the fact that it is in 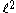.Optimal Estimates
The constant involved in the Hausdorff–Young inequality can be made optimal by using careful estimates from the theory of Harmonic AnalysisHarmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
. If
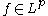for , the optimal bound is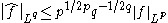where
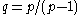is the Hölder conjugate of .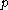